先要学会FFT[学习笔记]FFT——快速傅里叶变换
一、简介
FFT会爆精度。而且浮点数相乘常数比取模还大。
然后NTT横空出世了
虽然单位根是个好东西。但是,我们还有更好的东西
我们先选择一个模数,$constspace intspace p=998244353$
设g为p的单位根。这里就是3
那么有:$(omega_n^1)^n = g^{p-1}=1space mod space p$
那么,假设$x=(omega_n^1)$
其中一个解可以是:$x=g^{frac{p-1}{n}}$
在模意义之下,我们不妨用$g^{frac{p-1}{n}}$来代替$(omega_n^1)$
因为是g原根,所以0~n-1这n个次方取值都不相同,可以求出点值表示。
$omega_n^{-1}*omega_n^1=1$
那么$omega_n^{-1}=(g^{-1})^{frac{p-1}{n}}$
op的时候,把$g^{-1}$当做底数即可。
其他和FFT相同。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define int long long
using namespace std;
typedef long long ll;
il void rd(ll &x){
char ch;x=0;bool fl=false;
while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
for(x=numb;isdigit(ch=getchar());x=x*10+numb);
(fl==true)&&(x=-x);
}
namespace Miracle{
const int mod=998244353;
const int N=1e6+5;
const int G=3;
const int Gi=332748118;
int qm(int x,int y){
int ret=1;
while(y){
if(y&1) ret=(ll)ret*x%mod;
x=(ll)x*x%mod;
y>>=1;
}
return ret;
}
int n,m;
int a[4*N],b[4*N];
int r[4*N];
void NTT(int *f,int op){
for(reg i=0;i<n;++i){
if(i<r[i]){
swap(f[i],f[r[i]]);
}
}
for(reg p=2;p<=n;p<<=1){
int len=p/2;
ll tmp=qm(op==1?G:Gi,(mod-1)/p);
for(reg k=0;k<n;k+=p){
ll buf=1;
for(reg l=k;l<k+len;++l){
ll tt=(ll)buf*f[l+len]%mod;
f[l+len]=((ll)f[l]-tt);
if(f[l+len]<0) f[l+len]+=mod;
f[l]=((ll)f[l]+tt);
if(f[l]>=mod) f[l]-=mod;
buf=(ll)buf*tmp%mod;
}
}
}
}
void prin(int x){
if(x/10) prin(x/10);
putchar(x%10+'0');
}
int main(){
scanf("%d%d",&n,&m);
for(reg i=0;i<=n;++i){
rd(a[i]);
}
for(reg i=0;i<=m;++i){
rd(b[i]);
}
for(m=n+m,n=1;n<=m;n<<=1);
for(reg i=0;i<n;++i){
r[i]=r[i>>1]>>1|((i&1)?n>>1:0);
}
NTT(a,1);NTT(b,1);
for(reg i=0;i<n;++i) b[i]=(ll)b[i]*a[i]%mod;
NTT(b,-1);
ll inv=qm(n,mod-2);
for(reg i=0;i<=m;++i){
b[i]=(ll)b[i]*inv%mod;
prin(b[i]);putchar(' ');
}
return 0;
}
}
signed main(){
Miracle::main();
return 0;
}
/*
Author: *Miracle*
Date: 2018/11/21 19:01:08
*/
应用大前提:
1.多项式答案的系数不要太大,否则模数乘一下会爆long long,而且必须小于模数
2.多项式的长度不要太长。n<2^23
3.多项式系数必须是正整数!!(废话)
感觉NTT还是一个很好用的东西
常数小,
而且做题的时候,经常会给定模数。FFT一脸懵逼。
如果模数是一个k*2^m+1,并且满足2^m>n(多项式次数),那么可以直接像刚才一样计算。(原根找一下)
如果不是,中国剩余定理合并。
留坑。
二、多项式求逆:
推完式子之后,直接NTT做即可。
注意,
1.每次都要对位数取模,把位数限制在n以内。
2.计算长度为n的逆元的时候,必须算出来的是(n<<1)的多项式(因为H(x)*H(x)*F(x)是长度是n<<1的)
然后再砍掉n~(n<<1)-1的位数部分
可以都转化成点值表示,然后再求G(x)的点值表示。再插值

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=1e5+5; const int mod=998244353; const int GG=3; const int Gi=332748118; int n,m; int F[4*N],G[4*N],A[4*N],B[4*N],C[4*N]; int r[4*N]; int qm(int x,int y){ int ret=1; while(y){ if(y&1) ret=(ll)ret*x%mod; x=(ll)x*x%mod; y>>=1; } return ret; } void NTT(int *f,int op,int n){ for(reg i=0;i<n;++i){ if(i<r[i]) swap(f[i],f[r[i]]); } for(reg p=2;p<=n;p<<=1){ int len=p/2; int tmp=qm(op==1?GG:Gi,(mod-1)/p); for(reg k=0;k<n;k+=p){ int buf=1; for(reg l=k;l<k+len;++l){ int tt=(ll)buf*f[l+len]%mod; f[l+len]=(f[l]-tt+mod)%mod; f[l]=(f[l]+tt)%mod; buf=(ll)buf*tmp%mod; } } } if(op==1) return; int inv=qm(n,mod-2); for(reg i=0;i<n;++i) f[i]=(ll)f[i]*inv%mod; } void wrk(int n,int *a){ if(n==1){a[0]=qm(F[0],mod-2);return;} wrk(n>>1,a); for(reg i=0;i<n;++i) A[i]=F[i];//,B[i]=a[i]; for(reg i=n;i<(n<<1);++i) A[i]=0;//=B[i]=0; for(reg i=0;i<(n<<1);++i){ r[i]=r[i>>1]>>1|((i&1)?n:0); } NTT(A,1,(n<<1)),NTT(a,1,(n<<1)); for(reg i=0;i<(n<<1);++i){ a[i]=(2-(ll)A[i]*a[i]%mod+mod)%mod*a[i]%mod; } NTT(a,-1,(n<<1)); for(reg i=n;i<(n<<1);++i) a[i]=0; } int main(){ scanf("%d",&n); for(reg i=0;i<n;++i){ rd(F[i]);C[i]=F[i]; } int len; for(len=1;len<n;len<<=1); wrk(len,G); for(reg i=0;i<n;++i){ printf("%d ",G[i]); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/21 21:49:51 */
三、多项式除法
小学/初中奥数中有一种因式分解的方法,叫做长除法。
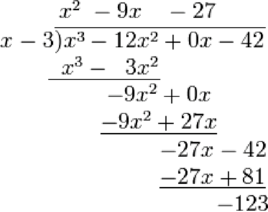
现在,我们终于可以用计算机实现了23333!!
直接那样做是O(n^2)的
但是我们有NTT和多项式求逆的工具。
具体方法是:
设$A_R(x)=x^n*A(frac{1}{x})$
(其实发现,$A_R(x)$的系数就是$A(x)$的系数$reverse$一下)
有:
$F(x)=Q(x)*G(x)+R(x)$
$F(frac{1}{x})=Q(frac{1}{x})*G(frac{1}{x})+R(frac{1}{x})$
$x^n*F(frac{1}{x})=x^{(n-m)}*Q(frac{1}{x})*x^m*G(frac{1}{x})+x^{n-m+1}*x^{m-1}*R(frac{1}{x})$
$F_R(x)=Q_R(x)*G_R(x)+x^{n-m+1}*R_R(x)$
那么一定有:
$F_R(x)=Q_R(x)*G_R(x)space mod space x^{n-m+1}$
$Q_R(x)=F_R(x)*G_R^{-1}space mod space x^{n-m+1}$
求出$G_R$的逆元(特别注意,这里的$G_R^{-1}$的次数是$n-m$,否则可能在$n-m>m$的时候,消不成),
然后就求出了$Q_R$
由于$Q_R$一共就$n-m+1$项,所以再翻转回来,就得到了$Q_R$了。
$F(x)=Q(x)*G(x)+R(x)$
所以:
$R(x)=F(x)-Q(x)*G(x)$
如果没算错的话,$R(x)$的次数一定小于$m$的
代码:

#include<bits/stdc++.h> #define reg register int #define il inline #define int long long #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(ll &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=1e5+5; const int mod=998244353; const ll GG=3; const ll Gi=332748118; int n,m; ll F[N],G[2*N],Q[2*N],R[N]; ll a[4*N],b[4*N],c[4*N],Gn[4*N]; int r[4*N]; ll qm(ll x,ll y){ ll ret=1; while(y){ if(y&1) ret=ret*x%mod; x=x*x%mod; y>>=1; } return ret; } void NTT(ll *f,int op,int n){ for(reg i=0;i<n;++i){ if(i<r[i]) swap(f[i],f[r[i]]); } for(reg p=2;p<=n;p<<=1){ int len=p/2; ll tmp=(op==1)?qm((ll)GG,(mod-1)/p):qm((ll)Gi,(mod-1)/p); for(reg k=0;k<n;k+=p){ ll buf=1; for(reg l=k;l<k+len;++l){ ll tt=buf*f[l+len]%mod; f[l+len]=(f[l]-tt+mod)%mod; f[l]=(f[l]+tt)%mod; buf=buf*tmp%mod; } } } } void mul(ll *a,ll *b,int n,int m){//clac A*B return b for(m=n+m-1,n=1;n<m;n<<=1); for(reg i=0;i<n;++i){ r[i]=r[i>>1]>>1|((i&1)?n>>1:0); } NTT(a,1,n);NTT(b,1,n); for(reg i=0;i<n;++i) b[i]=a[i]*b[i]%mod; NTT(b,-1,n); ll inv=qm(n,mod-2); for(reg i=0;i<n;++i) b[i]=b[i]*inv%mod; } void wrk(int n,ll *a){//clac ni if(n==1){ a[0]=qm(b[0],mod-2);return; } wrk(n>>1,a); for(reg i=0;i<n;++i)c[i]=b[i]; for(reg i=n;i<(n<<1);++i)c[i]=0; for(reg i=0;i<(n<<1);++i){ r[i]=r[i>>1]>>1|((i&1)?n:0); } NTT(c,1,((int)n<<1)); NTT(a,1,((int)n<<1)); for(reg i=0;i<(n<<1);++i){ a[i]=(2-(ll)a[i]*c[i]%mod+mod)%mod*a[i]%mod; } NTT(a,-1,(n<<1)); ll inv=qm((n<<1),mod-2); for(reg i=0;i<n;++i) a[i]=a[i]*inv%mod; for(reg i=n;i<(n<<1);++i) a[i]=0; } int main(){ scanf("%lld%lld",&n,&m); for(reg i=0;i<=n;++i) rd(F[i]),a[i]=F[i]; for(reg i=0;i<=m;++i) rd(G[i]),b[i]=G[i]; reverse(b,b+m+1); int len; for(len=1;len<n-m+1;len<<=1); wrk(len,Gn); // cout<<" bb "<<endl; // for(reg i=0;i<=m;++i){ // cout<<b[i]<<" "; // }cout<<endl; // cout<<" G-1 "<<endl; // for(reg i=0;i<=n-m;++i){ // cout<<Gn[i]<<" "; // }cout<<endl; reverse(a,a+n+1); for(reg i=n-m+1;i<=n;++i) a[i]=0; for(reg i=n-m+1;i<=m;++i) Gn[i]=0; // cout<<" FR "<<endl; // for(reg i=0;i<=n-m;++i){ // cout<<a[i]<<" "; // }cout<<endl; mul(Gn,a,n-m+1,n-m+1); // cout<<" QR "<<endl; // for(reg i=0;i<=n-m;++i){ // cout<<a[i]<<" "; // }cout<<endl; reverse(a,a+n-m+1); for(reg i=0;i<n-m+1;++i) Q[i]=a[i],printf("%lld ",Q[i]); puts(""); mul(Q,G,n-m+1,m+1); for(reg i=0;i<m;++i){ R[i]=(F[i]-G[i]+mod)%mod; printf("%lld ",R[i]); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/22 17:15:16 */
四、任意模数NTT

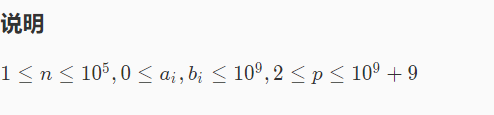
常用的解法是这样的:
答案小于10^23
取3个模数const ll m1 = 469762049, m2 = 998244353, m3 = 1004535809;
每个模数都是a*2^k+1并且k够用
m1*m2*m3>10^23
所以答案在mod m1*m2*m3下的结果就是答案
对三个质数分别做一次NTT
然后对每个系数依次用CRT合并
合并的时候,为了防止爆long long:

补充:
所有过程不涉及log^2n的快速幂快速乘,
而且最后的k*M+A一定小于m1*m2*m3,并且三个同余方程都满足
所以可以直接对p取模了。
代码:

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=2e5+5; const int G=3; const ll m1 = 469762049, m2 = 998244353, m3 = 1004535809; int n,m,p; ll a[2*N],b[2*N],f[3][4*N],g[4*N]; ll add(ll x,ll y,ll mod){ return x+y>=mod?x+y-mod:x+y; } ll qk(ll x,ll y,ll mod){ x%=mod;y%=mod; ll ret=0; while(y){ if(y&1) ret=add(ret,x,mod); x=add(x,x,mod); y>>=1; } return ret; } ll qmo(ll x,ll y,ll mod){ ll ret=1; x%=mod; while(y){ if(y&1) ret=ret*x%mod; x=x*x%mod; y>>=1; } return ret; } int rev[4*N]; void NTT(ll *f,int n,int c,ll mod){ ll GI=qmo(G,mod-2,mod); for(reg i=0;i<n;++i){ if(i<rev[i]) swap(f[i],f[rev[i]]); } for(reg p=2;p<=n;p<<=1){ ll gen; int len=p/2; if(c==1) gen=qmo(G,(mod-1)/p,mod); else gen=qmo(GI,(mod-1)/p,mod); for(reg l=0;l<n;l+=p){ ll buf=1; for(reg k=l;k<l+len;++k){ ll tmp=buf*f[k+len]%mod; f[k+len]=(f[k]-tmp+mod)%mod; f[k]=(f[k]+tmp)%mod; buf=buf*gen%mod; } } } } void clac(ll *f,ll *g,int n,ll mod){ NTT(f,n,1,mod);NTT(g,n,1,mod); for(reg i=0;i<n;++i) f[i]=f[i]*g[i]%mod; NTT(f,n,-1,mod); ll inv=qmo(n,mod-2,mod); for(reg i=0;i<n;++i) f[i]=f[i]*inv%mod; } int main(){ rd(n);rd(m);rd(p); for(reg i=0;i<=n;++i) scanf("%lld",&a[i]),f[0][i]=a[i]; for(reg j=0;j<=m;++j) scanf("%lld",&b[j]),g[j]=b[j]; for(m=n+m,n=1;n<=m;n<<=1); for(reg i=0;i<n;++i){ rev[i]=(rev[i>>1]>>1)|((i&1)?n>>1:0); } clac(f[0],g,n,m1); for(reg i=0;i<n;++i) g[i]=b[i],f[1][i]=a[i]; clac(f[1],g,n,m2); for(reg i=0;i<n;++i) g[i]=b[i],f[2][i]=a[i]; clac(f[2],g,n,m3); for(reg i=0;i<=m;++i){ ll A=(qk(qk(f[0][i],m2,m1*m2),qmo(m2,m1-2,m1),m1*m2)+qk(qk(f[1][i],m1,m1*m2),qmo(m1,m2-2,m2),m1*m2))%(m1*m2); // cout<<" AA "<<A<<endl; ll K=(f[2][i]-A%m3+m3)%m3*qmo(m1*m2%m3,m3-2,m3)%m3; // cout<<" KK "<<K<<endl; ll op=(K*m1%p*m2%p+A%p)%p; printf("%lld ",op); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2019/1/9 21:23:11 */
