题意:
有四种操作
0操作 清空所有点
1操作 在(x,y)处插入一个带颜色的点
2 操作统计(1~x)(y1~y2)这个范围的不同的颜色数
3 结束
思路:
颜色数只有51个
我们可以建51颗线段树 因为每次查询都是1~x范围的 所以我们对于每个颜色的线段树
维护y轴的区间 节点的值维护区间最小的x
对于每次查询 我们就只需要查询 每种颜色是否有<=x的点即可
关于剪枝:
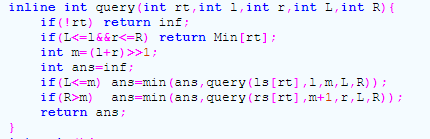 TLE
TLE
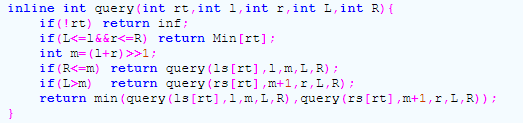 7784MS
7784MS
 5584MS
5584MS

#include<bits/stdc++.h> using namespace std; #define ll long long #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define inf 0x3f3f3f3f const int maxn = 1000000+5; int cnt,x,fg; int ls[maxn*4],rs[maxn*4],Min[maxn*4],root[60]; inline void init(){ memset(root,0,sizeof(root)); ls[0]=0;rs[0]=0;Min[0]=inf;cnt=0; } inline void push_up(int rt){ Min[rt]=min(Min[ls[rt]],Min[rs[rt]]); } inline void update(int &rt,int l,int r,int L,int val){ if(!rt){ rt=++cnt; ls[rt]=0;rs[rt]=0;Min[rt]=val; } if(l==r){ Min[rt]=min(Min[rt],val); return ; } int m=(l+r)>>1; if(L<=m) update(ls[rt],l,m,L,val); else update(rs[rt],m+1,r,L,val); push_up(rt); } inline void query(int rt,int l,int r,int L,int R){ if(fg||!rt) return ; if(L<=l&&r<=R) { if(Min[rt]<=x) fg=1; return ; } int m=(l+r)>>1; if(L<=m) query(ls[rt],l,m,L,R); if(R>m) query(rs[rt],m+1,r,L,R); } int main(){ int op,y,c,l,r; int n=maxn; while(~scanf("%d",&op)){ if(op==3) break; if(op==0){ init(); }else if(op==1){ scanf("%d %d %d",&x,&y,&c); update(root[c],1,n,y,x); }else { scanf("%d %d %d",&x,&l,&r); int ans=0; for(int i=0;i<=50;i++){ fg=0; query(root[i],1,n,l,r); ans+=fg; } printf("%d ",ans); } } return 0; }
距离省赛越来越近 又要被暴打了(大雾)
