摩尔投票法简介

引言

---

今天又做到了 Leetcode 169. 多数元素 这一道题. 我依稀记得最优的解法叫做什么摩尔投票法. 但是我对它的印象竟然只有这个名字本身了 Orz. 对于这个算法本身倒是忘得一干二净. 于是我打算系统性地学习一下这个算法的原理, 并将它总结出来写成这篇博客. 不知道在哪里看到的一句话 :

当你开始教别人的时候, 你就真的掌握它了

所以, 我今天在这里打算跟大家分享这个算法, 并试图以浅显的语言让你也学会这个方法, 那么让我们开始吧

先从简单的方法开始聊起

如果从来没有听说过摩尔投票法, 我们会如何尝试解决这个问题, 起码要有下面的思路:

1. 用空间换时间, 也就是用一个哈希表把每个元素出现的次数记下来, 然后我们再检查一遍我们的哈希表并找到其中出现次数大于 \(\lfloor n/2\rfloor\) 的就可以.这样时间复杂度和空间复杂度都是 \(O(n)\)
2. 尝试对数组进行排序, 因为我们要找的元素超过了数组一半的长度, 这意味着它一定会出现在数组的中间位置. 这个也不难想到, 但是用排序的话虽然空间复杂度是 \(O(1)\), 但是时间复杂度还是大于 \(O(n)\) 的, *比如如果你采用的是快速排序的话, 时间复杂度就是 \(O(nlogn)\)

那么有没有一种方法可以做到时间复杂度是 \(O(n)\), 空间复杂度是 \(O(1)\) 呢? 也就是结合了上面两个方法的优点. 有的, 答案就是摩尔投票法 !

摩尔投票法

---

问题描述: 假设我们的数组有 \(n\) 个元素, 我们要找到其中出现次数超过一半的元素

算法流程:

1. 从这 \(n\) 个元素中选一个作为 candidate，记录它的票数为 votes = 1.

2. 此时我们的数组中还有 \(n-1\) 个元素, 我们每次都取出一个元素(记为 current), 并重复执行以下的步骤(一共 n-1 次)

   1. 将它和我们当前的 candidate 做比较, 如果它们的值一样, 那么 votes++, 也就是投赞同票
   2. 如果它们的值不一样, votes--, 也就是投反对票. 如果此时 votes = 0 的话, 那么 candidate <- current, 也就是说我们让 current 成为了新的 candidate, 并记 votes = 1

3. 最后 candidate 的值就可能是我们想要的出现次数超过一半的元素, 此时我们得再遍历一遍数组进行计数看它到底是不是

在看完上面的算法流程之后, 你可能跟我一样感到很困惑. 为什么这样最后我们就能找到出现次数超过一半的元素. 其实只要想明白一个原理就很简单

出现次数超过 \(\lfloor n/2\rfloor\) 次的元素如果存在, 此时数组中的其他元素一定是出现次数小于 \(\lfloor n/2\rfloor\) 的

这句话有什么用呢 ?

因为摩尔投票法的做法其实就是投票

• 可以是投赞同票, 此时相当于我们在统计这个元素出现的次数
• 可以是投反对票. 相当于我们撤销了一个同意票, 就是抵消抵消抵消!!!

但是因为出现次数超过一半的元素加起来的票数(赞同票) > 剩下所有不是的(反对票)这件事是一定成立的, 所以无论怎样最后赢的永远是出现次数超过一半的元素. 于是我们就找到了

如果还是不懂可以看看下面的这个 GIF 图理解一下~

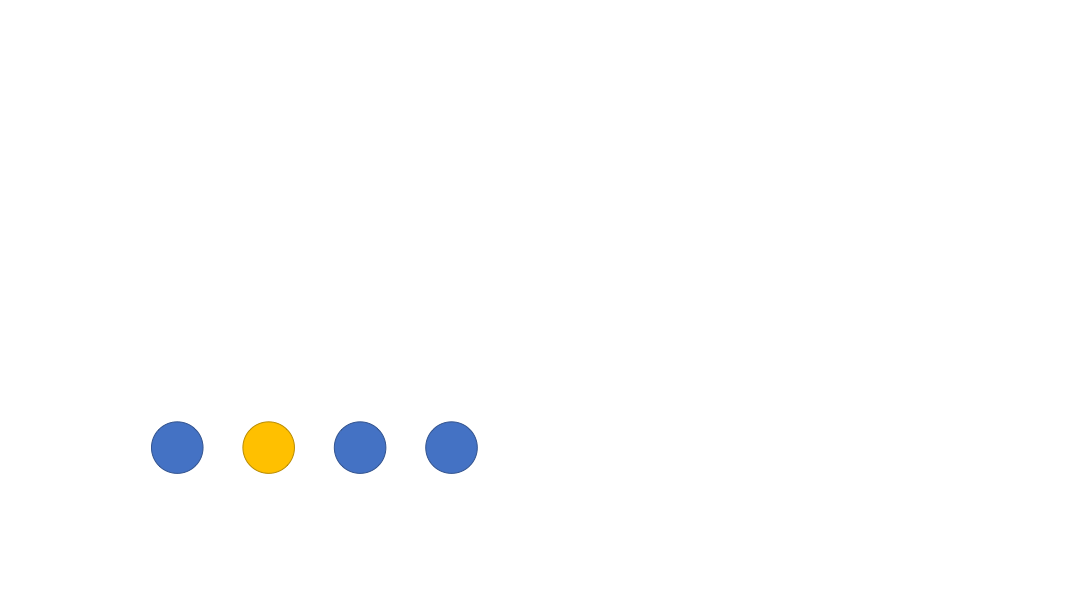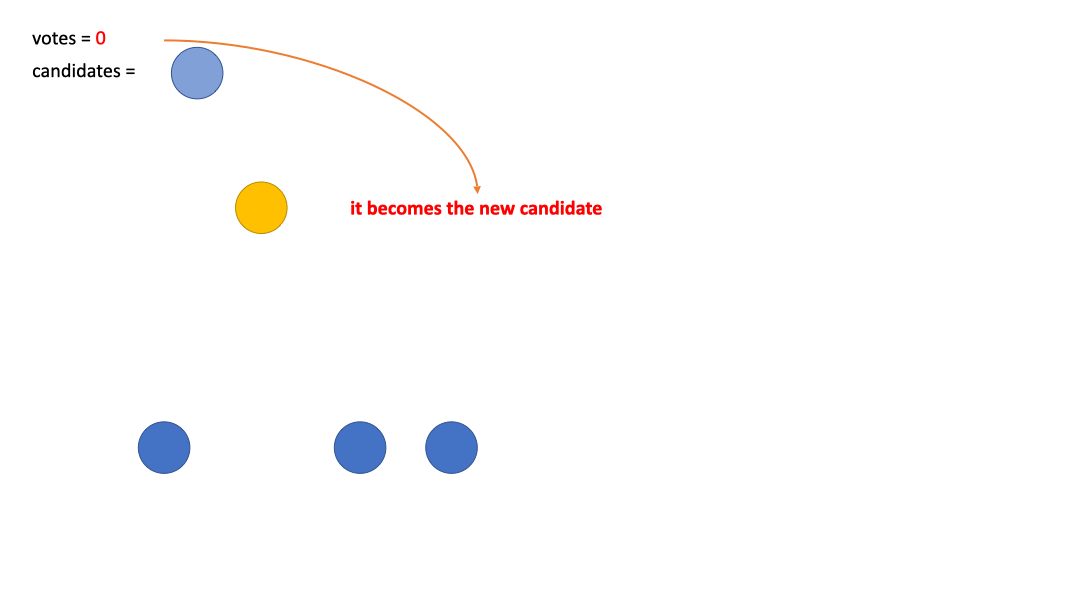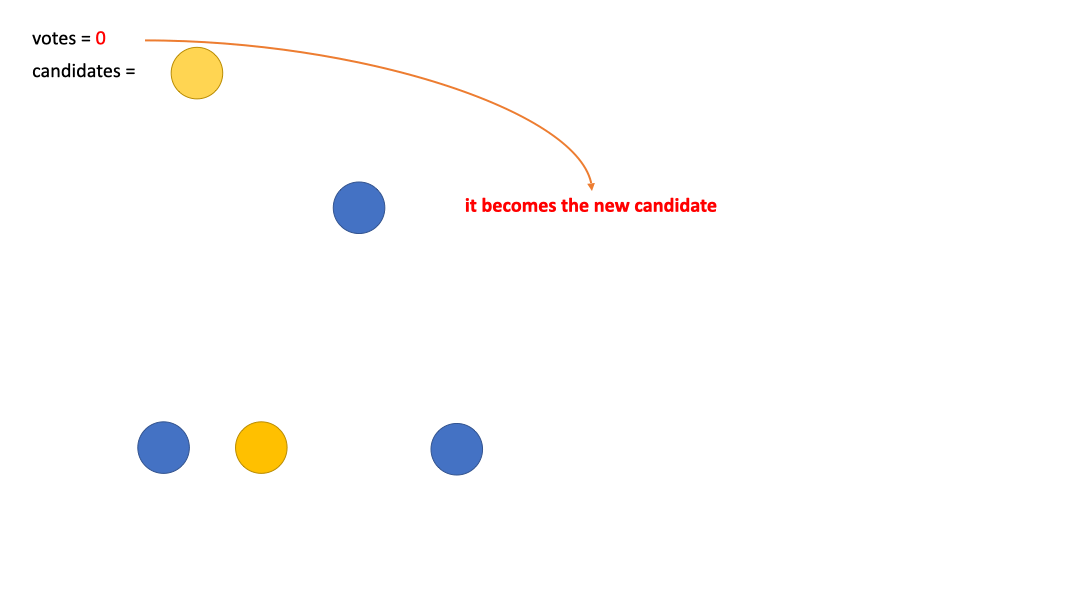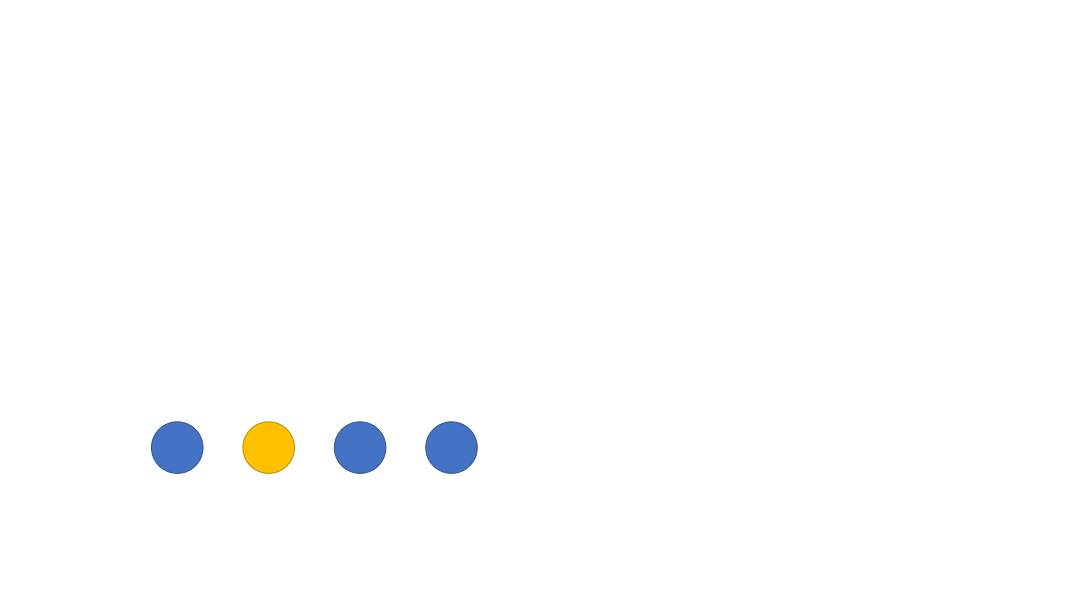
代码

---

class Solution {
    public int majorityElement(int[] nums) {
        if (nums.length < 2) {
            return nums[0]; 
        }
        int candidates = nums[0];
        int votes = 1;
        // step 1. start to vote
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != candidates) {
                votes -= 1;
                if (votes == 0) {
                    candidates = nums[i];
                    votes = 1;
                }
            } else {
                votes += 1;
            }
        }
        // step2. check
        int occurs = 0;
        for (var val: nums) {
            if (candidates == val) {
                occurs += 1;
            }
        }
        if (occurs >= nums.length / 2) {
            return candidates;
        } else {
            return -1;
        }
    }
}

FAQ

---

Q: 为什么还需要第二轮检查呢? 能不能直接看 votes 呢?

A: 不能, 首先这个「出现次数超过一半」的元素不一定存在. 比如 [1,2,3]. 另外就算它存在, 遍历完数组之后, 此时 votes 也不一定是它的真实票数. 比如 [1, 2, 2, 2, 3] 最后 3 会投反对票导致 votes - 1