摸底测试链接http://oj.jxust.edu.cn/contest?id=1702
A.Water
思路:题面说的是随机操作,但是实际上只是输入数据随机,操作的时候怎么操作都是可以的,只需要用数组存一下每个水瓶倒多少水,然后从第一个开始往后倒,如果有多就传给下一个瓶子,如果不够就直接全部赋给这一个瓶子就行了。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; LL a[100005], b[100005], ans[100005]; int main() { LL t, n, m, x, y; scanf("%lld", &t); while(t--) { scanf("%lld%lld", &n, &m); for(int i = 1;i <= n;i++) { scanf("%lld", &a[i]); b[i] = 0; } for(int i = 1;i <= m;i++) { scanf("%lld%lld", &x, &y); b[x] += y; } for(int i = 1;i <= n;i++) { if(b[i] >= a[i]) { ans[i] = a[i]; b[i] -= a[i]; //printf("ai = %d ", a[i]); //printf("ansi = %d ", ans[i]); b[i+1] += b[i]; } else { ans[i] = b[i]; b[i] = 0; } } for(int i = 1;i <= n;i++) { if(i < n) printf("%lld ", ans[i]); else printf("%lld ", ans[i]); } } return 0; }
B.Prime Split
思路:数据范围是4e4,素数只有4000多个,直接n^2复杂度枚举两个素数然后判断一下第三个数是不是素数就行了,但是要注意重复的情况,枚举的时候保证第二个素数不小于第一个素数,然后当第二个素数 >= 第一个素数 && 第三个素数大于第一个素数的时,ans--。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; int s[5005], vis[40005]; bool sushu(int x) { for(int i = 2;i*i <= x;i++) { if(x%i == 0) return false; } return true; } int main() { int t, n, temp; scanf("%d", &t); int cnt = 0; for(int i = 2;i < 40000;i++) { if(sushu(i)) { s[cnt++] = i; vis[i] = 1; } } while(t--) { int ans = 0; scanf("%d", &n); for(int i = 0;i < cnt;i++) { for(int j = i;j < cnt;j++) { if(n-s[i]-s[j] <= 1) break; //printf("%d %d %d ", n,s[i], s[j]); temp = n-s[i]-s[j]; if(vis[temp]) { ans++; //printf("%d %d %d %d ", n,s[i], s[j], temp); if(s[j] >= s[i] && temp > s[i]) { ans--; //printf("%d %d %d %d ", n,s[i], s[j], temp); } } } if(n - s[i] <= 2) break; } printf("%d ", ans); } return 0; }
C.Connect
思路:有点绕的最小生成树,用结构体存一下x,y,z,和这是第几个点,再给x,y,z分别排一次序,相邻的点相减得到的边作为kruskal的边,然后就是n个点,3n-3条边的kruskal了。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; int c[200005]; struct bian { int val, st, en; }b[600006]; struct node { int x, y, z, num; }a[600005]; bool cmp(node a, node b) { return a.x<b.x; } bool cmpp(node a, node b) { return a.y<b.y; } bool cmppp(node a, node b) { return a.z<b.z; } bool cmpppp(bian a, bian b) { return a.val<b.val; } int Find(int x) { if(x == c[x]) return x; return c[x] = Find(c[x]); } void Union(int x, int y) { x = Find(x); y = Find(y); if(x == y) return; c[x] = y; } int kruskal(int n, int m) { int sum = 0, res = 0; for(int i = 0;i < m && sum != n-1;i++) { if(Find(b[i].st) != Find(b[i].en)) { Union(b[i].st, b[i].en); res += b[i].val; sum++; } } return res; } int main() { int n, x, xx, y, yy, z, zz, temp; scanf("%d", &n); for(int i = 0;i < n;i++) { scanf("%d%d%d", &xx, &yy, &zz); c[i+1] = i+1; a[i].x=xx, a[i].y=yy, a[i].z=zz, a[i].num=i+1; } int cnt = 0; sort(a, a+n, cmp); for(int i = 0;i < n-1;i++) { temp = a[i+1].x - a[i].x; b[cnt].val = temp, b[cnt].st = a[i].num, b[cnt].en = a[i+1].num; cnt++; } sort(a, a+n, cmpp); for(int i = 0;i < n-1;i++) { temp = a[i+1].y - a[i].y; b[cnt].val = temp, b[cnt].st = a[i].num, b[cnt].en = a[i+1].num; cnt++; } sort(a, a+n, cmppp); for(int i = 0;i < n-1;i++) { temp = a[i+1].z - a[i].z; b[cnt].val = temp, b[cnt].st = a[i].num, b[cnt].en = a[i+1].num; cnt++; } sort(b, b+cnt, cmpppp); int ans = kruskal(n, n*3-3); printf("%d ", ans); return 0; }
E.Number
思路:求n模x的逆元,将n分解为若干个正整数之和,使得这些正整数的乘积x最大,n%3 == 0时分成若干个3,余1时把一个3变成4,余2时多一个2。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; LL x, y, n, temp; void exoj(LL a, LL b) { if(b == 0) { x = 1; y = 0; return; } exoj(b, a%b); LL t = x; x = y; y = t-(a/b)*y; return; } int main() { temp = 1; scanf("%lld", &n); if(n%3 == 0) { for(int i = 1;i <= n/3;i++) temp *= 3; } else if(n%3 == 1) { for(int i = 1;i < n/3;i++) temp *= 3; temp *= 4; } else { for(int i = 1;i < n/3;i++) temp *= 3; temp *= 6; } exoj(n, temp); printf("%lld ", (x+temp)%temp); return 0; }
F.操作数
思路:线段树延迟标记,然后查询单点。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; const int maxn = 111111; int lazy[maxn*4]; int SegTree[maxn*4]; void Pushdown(int root, int l, int r) { lazy[root*2] += lazy[root]; lazy[root*2+1] += lazy[root]; SegTree[root*2] += lazy[root]; SegTree[root*2+1] += lazy[root]; lazy[root] = 0; } void query(int root, int nstart, int nend, int index) { if(nstart > index || nend < index) return; if(nstart == nend) { if(SegTree[root]%2 == 0) { printf("0 "); return; } else { printf("1 "); return; } } if(lazy[root]) Pushdown(root, nstart, nend); int mid = (nstart + nend)/2; if(mid >= index) query(root*2, nstart, mid, index); if(mid < index) query(root*2+1, mid+1, nend, index); } void update(int root, int nstart, int nend, int l, int r) { if(l > nend || r < nstart) return; if(l <= nstart && r >= nend) { lazy[root]++; SegTree[root]++; return; } if(lazy[root]) Pushdown(root, nstart, nend); int mid = (nstart + nend)/2; if(mid >= l) update(root*2, nstart, mid, l, r); if(mid < r) update(root*2+1, mid+1, nend, l, r); } int main() { int n, m, t, L, R, i; scanf("%d%d", &n, &m); while(m--) { scanf("%d",&t); if(t == 1) { scanf("%d%d", &L, &R); if(L > R) swap(L, R); update(1, 1, n, L, R); } else { scanf("%d", &i); query(1, 1, n, i); } } return 0; }
G.聚会
思路:组合数二项式定理,推出公式后一个快速幂就解决。
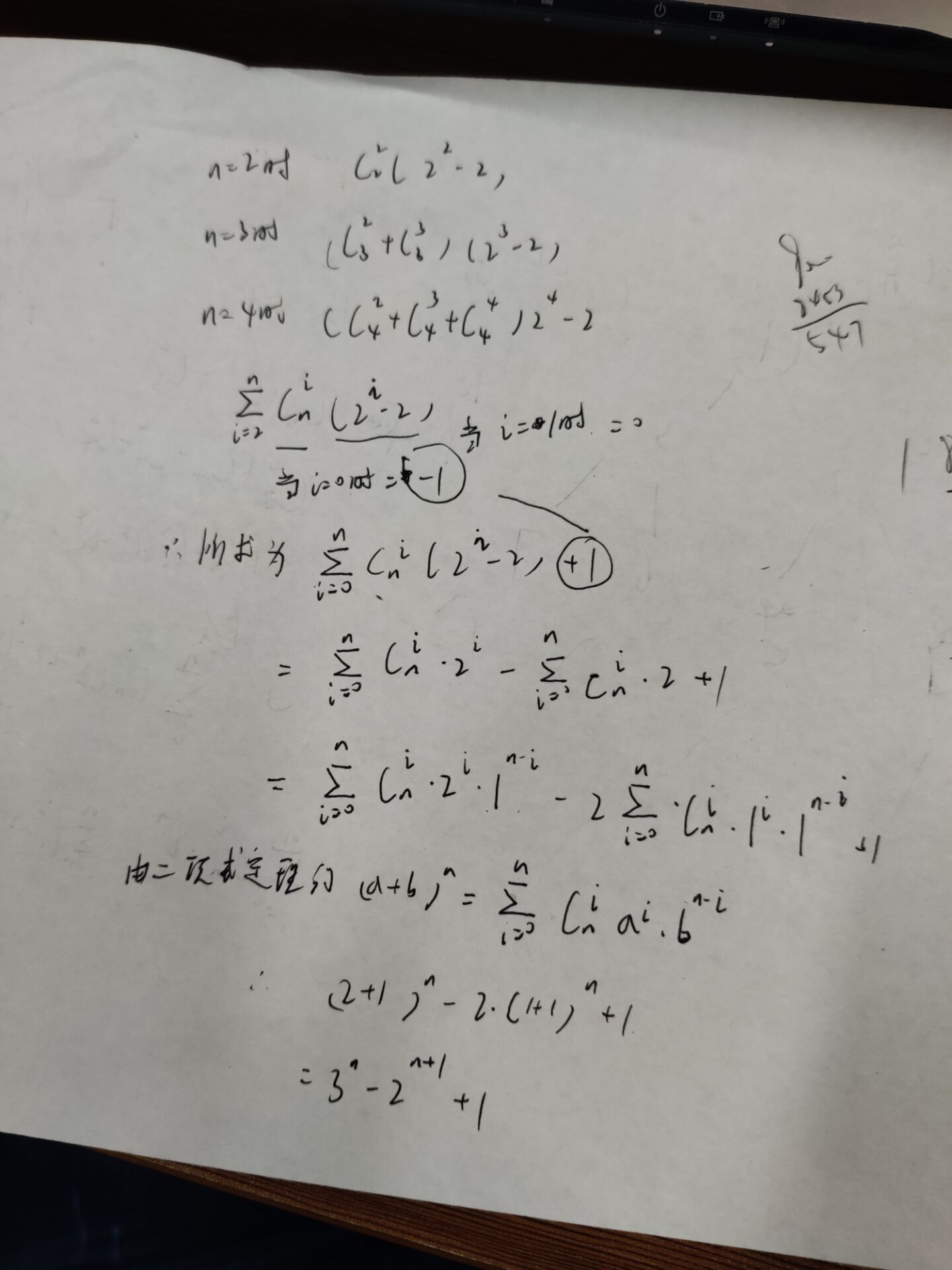

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; LL a[100005], b[100005]; LL inv(LL a, LL b) { if(a==0) return 1; LL res = 1; b = b-2; while(b) { if(b&1) res = res%MOD*a%MOD; a = a%MOD*a%MOD; b >>= 1; } return res; } int main() { LL n, ans, temp = 1, tt = 2; for(int i = 2;i <= 1e5;i++) { temp = temp*i%MOD; a[i] = temp; tt = tt*2%MOD; b[i] = tt; } while(scanf("%lld", &n)!=EOF){ ans = 0; if(n == 1) { printf("0 "); return 0; } for(int i = 2;i <= n;i++) { ans += a[n]*inv(a[i], MOD)%MOD*inv(a[n-i], MOD)%MOD*(b[i]-2)%MOD; ans = ans%MOD; } printf("%lld ", ans); } return 0; }
H.地图
思路:走三遍bfs,前两遍走输入数据,第三遍把前两个地图的障碍物加在一起,如果前两次的步数一样第三次把障碍物加在一起之后也能走通且步数和前两次一样就是YES。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; int vis[505][505]; int dir[4][2]={1,0, 0,1, -1,0, 0,-1}; int n, m; char s[505][505], ss[505][505]; struct node { int x, y, val; }; queue<node> q; node road[505][505]; int bfs(node t, char s[][505]) { while(!q.empty()) q.pop(); memset(vis, 0, sizeof(vis)); vis[0][0] = 1; q.push(t); node Next, temp; while(!q.empty()) { temp = q.front(); q.pop(); if(temp.x == n-1 && temp.y == m-1) return temp.val; for(int i = 0;i < 4;i++) { Next.x = temp.x + dir[i][0]; Next.y = temp.y + dir[i][1]; if(vis[Next.x][Next.y] == 0 && Next.x >= 0&& Next.x < n && Next.y >= 0 && Next.y < m && s[Next.x][Next.y] == '.') { Next.val = temp.val + 1; q.push(Next); vis[Next.x][Next.y] = 1; } } } return -1; } int main() { scanf("%d%d", &n, &m); node t; t.x = 0, t.y = 0, t.val = 0; for(int i = 0;i < n;i++) scanf("%s", s[i]); int flag1 = bfs(t, s); for(int i = 0;i < n;i++) { scanf("%s", ss[i]); for(int j = 0;j < m;j++) { if(ss[i][j] == '#') s[i][j] = '#'; } } int flag2 = bfs(t, ss); int flag3 = bfs(t, s); if(flag1 == flag2 && flag1 == flag3 && flag1 >= 0) printf("YES "); else printf("NO "); return 0; }
I.我是签到题
思路:两边走,哪边小就把另一边的字母化成这边这个小的字母。

#include<bits/stdc++.h> #include<vector> #include<map> #include<queue> #define LL long long #define INF 0x3f3f3f3f #define MOD 1000000007 using namespace std; char s[100005]; int main() { scanf("%s", s); int len = strlen(s); int n = len/2; for(int i = 0,j = len-1;i < n;i++,j--) { if(s[i] < s[j]) s[j] = s[i]; else s[i] = s[j]; } for(int i = 0;i < len;i++) printf("%c", s[i]); return 0; }
