Gonzalez R. C. and Woods R. E. Digital Image Processing (Forth Edition)
基本
酉变换
一维的变换:
[mathbf{t} = mathbf{A} mathbf{f}, \
mathbf{f} = mathbf{A}^{H} mathbf{t}, \
mathbf{A}^H = {mathbf{A}^*}^{T}, mathbf{A}^Hmathbf{A} = mathbf{I}.
]
以及二维的变换:
[mathbf{T} = mathbf{A} mathbf{F} mathbf{B}^T, \
mathbf{F} = mathbf{A}^H mathbf{T} mathbf{B}^*, \
mathbf{A}^Hmathbf{A=I}, mathbf{B}^{T}mathbf{B}^* =mathbf{I}.
]
以一维的为例, 实际上就是
[t_u = sum_{x = 0}^{N-1} f_x s(x, u) = mathbf{f}^T mathbf{s}_u, u=0,1,cdots, N-1,\
mathbf{s}_u = [s(0, u), s(1, u), cdots, s(N-1, u)]^T.
]
故
[mathbf{A} = [mathbf{s}_0, cdots, mathbf{s}_{N-1}]^{T}.
]
注: 下面假设:(N=2^n).
[s(x, u) = frac{1}{sqrt{N}} (-1)^{sum_{i=0}^{n-1}b_i(x)b_i(u)},
]
注意, 这里(b_i(u))表示(u)的二进制的第(i)位, 比如(4)的二进制为(100), 此时(b_0 = 0, b_2=1).
变换矩阵可以通过更通俗易懂的方式搭建:
[mathbf{A}_W = frac{1}{sqrt{N}} mathbf{H}_N, \
mathbf{H}_{2N} =
left [
�egin{array}{cc}
mathbf{H}_N & mathbf{H}_N \
mathbf{H}_N & -mathbf{H}_N \
end{array}
ight ], \
mathbf{H}_{2} =
left [
�egin{array}{cc}
1 & 1 \
1 & -1 \
end{array}
ight ].
]
sequency-ordered WHT
[mathbf{H}_{4} =
left [
�egin{array}{cc}
1 & 1 & 1 & 1\
1 & -1 & 1 & -1 \
1 & 1 & -1 & -1\
1 & -1 & -1 & 1 \
end{array}
ight ].
]
可以发现, 第1行((u=0, 1, 2, 3))的符号变换最快的(类似与DFT中的频率的概念), 故sequency-order, 即按照符号变换快慢的递增排列, 其公式如下:
[s(x, u) = frac{1}{sqrt{N}}(-1)^{sum_{i=0}^{n-1}b_i(x)p_i(u)}, \
p_0 (u) = b_{n-1}(u), \
p_{n-1-i}(u) = b_i(u) + b_{i+1}(u), quad i = 0, cdots, n-2.
]
记(mathbf{H}_{W'})为sequency-order的, 则 (mathbf{H}_{W'})的第(u)行与(mathbf{H}_{W})的第(v)行存在如下的关系:
- 考虑(n)bit的二进制, 则
[u: (u_{n-1}u_{n-2}cdots u_0),\
v: (v_{n-1}v_{n-2}cdots v_0).
]
- 将(u)转换成其gray code格式
[g_i = u_i oplus u_{i+1}, quad i=0, cdots, n-2\
g_{n-1} = s_{n-1}.
]
其中(oplus)表示异或操作.
3. 对(g)进行bit-reverse, 即(g_i, g_{n-1-i})调换位置, 则
[v_i = g_{n-1-i}.
]
举个例子, 假设(n=3), (u=4 = (100)_2), 则(g = (110)_2), (v=(011)_2 = 3). 即(H_8')的第4行为(H_8)的第3行(注意均从0开始计数).
proof:
[�egin{array}{ll}
p_{n-1-i}(u)
&= b_i(u) + b_{i+1}(u) \
&Leftrightarrow b_i(g) \
&= b_{n-1-i}(v).
end{array}
]
注意(Leftrightarrow), 是这样的, (b_i + b_{i+1})仅有(0, 1, 2)三种可能性, 而((-1)^1=-1)否则为1,而(b_i(g)=1)恰好是(b_i(u) + b_{i+1}(u) = 1) (根据异或的定义可得), 故可能等价替换.
[p_0(u) = b_0(v),
]
是显然的, 证毕.
下图便是按照sequency增序的表示.

[mathbf{A}_{SI} = frac{1}{sqrt{N}}mathbf{S}_N, \
mathbf{S}_{N} =
left [
�egin{array}{cccccc}
1 & 0 & mathbf{0} & 1 & 0 & mathbf{0} \
a_N & b_N & mathbf{0} & -a_N & b_N & mathbf{0} \
0 & 0 & mathbf{I}_{(N/2)-2} & 0 & 0 & mathbf{I}_{(N/2)-2} \
0 & 1 & mathbf{0} & 0 & -1 & mathbf{0} \
-b_N & a_N & mathbf{0} & b_N & a_N & mathbf{0} \
0 & 0 & mathbf{I}_{(N/2)-2} & 0 & 0 & mathbf-{I}_{(N/2)-2} \
end{array}
ight ]
left [
�egin{array}{cc}
mathbf{S}_{N/2} & mathbf{0} \
mathbf{0} & mathbf{S}_{N/2} \
end{array}
ight ], \
mathbf{S}_2 =
left [
�egin{array}{cc}
1 & 1 \
1 & -1 \
end{array}
ight ], \
a_N = [frac{3N^2}{4(N^2-1)}]^{1/2}, \
b_N = [frac{N^2-4}{4(N^2-1)}]^{1/2}.
]
标准正交性质是容易证明的, 需要特别注意的是, 改变换矩阵是非对称的, 所以逆变换是需要计算逆的(A_{SI}^{-1}).

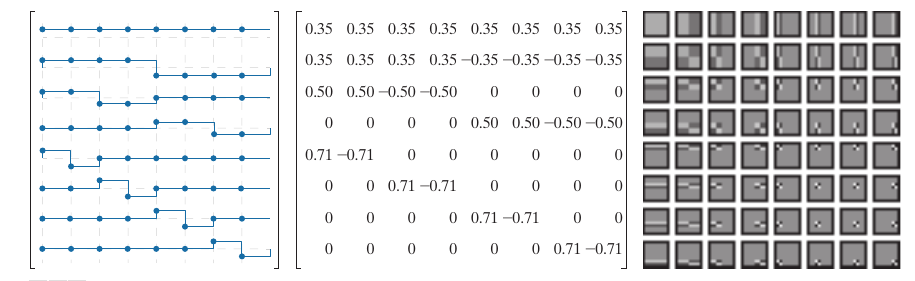
Haar 是一种小波变换, 这里简单写一下.
[s(x, u) = frac{1}{sqrt{N}} h_u(x / N), quad x= 0,1,cdots, N-1, \
u = 2^p + q, \
h_u(x) =
left {
�egin{array}{ll}
1 & u=0 : ext{and} : 0 le x < 1, \
2^{p/2} & u > 0 ext{and} : q/2^p < (q + 0.5)/2^p, \
-2^{p/2} & u > 0 ext{and} : (q+0.5)/2^p < (q + 1)/2^p, \
0 & ext{otherwise}.
end{array}
ight .
]