李航《统计学习方法》CH03

CH03 k近邻法

前言

章节目录

1. k近邻算法
2. k近邻模型
   1. 模型
   2. 距离度量
   3. k值选择
   4. 分类决策规则
3. k近邻法的实现: KDTree
   1. 构造KDTree
   2. 搜索KDTree

导读

kNN是一种基本分类与回归方法.

• 0-1损失函数下的经验风险最小化
• kNN的k和KDTree的k含义不同,
• KDTree是一种存储k维空间数据的树结构
• 建立空间索引的方法在点云数据处理中也有广泛的应用，KDTree和八叉树在3D点云数据组织中应用比较广
• KDTree是二叉树
• 另外，书中的KDTree实现的时候针对了一种k=1的特殊的情况

最近邻算法

k=1的情形, 称为最近邻算法. 书中后面的分析都是按照最近邻做例子, 这样不用判断类别, 可以略去一些细节.

k近邻模型

距离度量

特征空间中的两个实例点的距离是两个实例点相似程度的反映。

书中是如上描述的，这里要注意距离越近(数值越小), 相似度越大。

这里用到了$L_p$距离, 可以参考Wikipedia上$L_p$ Space词条

1. p=1 对应 曼哈顿距离
2. p=2 对应 欧氏距离
3. 任意p 对应 闵可夫斯基距离

$$L_p(x_i, x_j)=left(sum_{l=1}^{n}{left|x_{i}^{(l)}-x_{j}^{(l)} ight|^p} ight)^{frac{1}{p}}$$

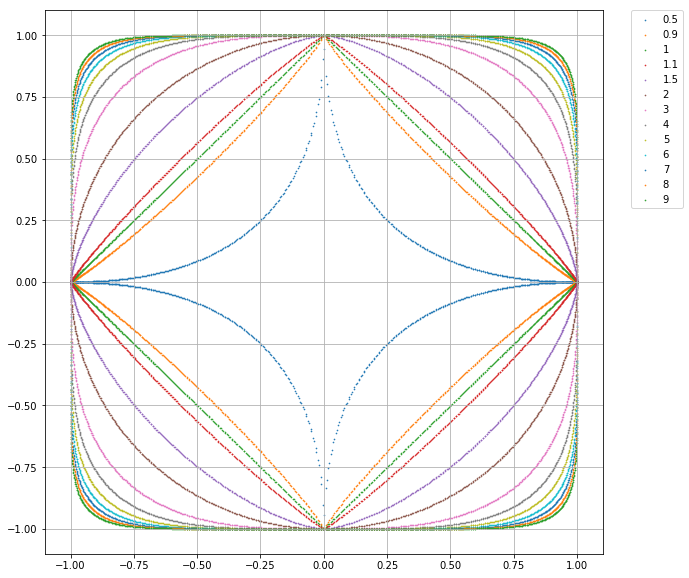
考虑二维的情况, 上图给出了不同的p值情况下与原点距离为1的点的图形. 这个图有几点理解下:

1. 与原点的距离
2. 与原点距离为1的点
3. 前一点换个表达方式, 图中的点向量($x_1$, $x_2$)的p范数都为1
4. 图中包含多条曲线, 关于p=1并没有对称关系
5. 定义中$pgeqslant1$，这一组曲线中刚好是凸的

这里要补充一点：

范数是对向量或者矩阵的度量，是一个标量，这个里面两个点之间的$L_p$距离可以认为是两个点坐标差值的p范数。

参考下例题3.1的测试案例，这个实际上没有用到模型的相关内容。

k值选择

1. 关于k大小对预测结果的影响, 书中给的参考文献是ESL, 这本书还有个先导书叫ISL.
2. 通过交叉验证选取最优k
3. 二分类问题, k选择奇数有助于避免平票

分类决策规则

Majority Voting Rule

误分类率

$frac{1}{k}sum_{x_iin N_k(x)}{I(y_i e c_i)}=1-frac{1}{k}sum_{x_iin N_k(x)}{I(y_i= c_i)}$

如果分类损失函数是0-1损失, 误分类率最低即经验风险最小.

关于经验风险, 参考书上CH01第一章 (1.11)和(1.16)

实现

kNN在实现的时候，要考虑多维数据的存储，这里会用到树结构。

在Scipy Cookbook里面有个kd树具体的实现^2可参考

构造KDTree

KDTree的构建是一个递归的过程

注意KDTree左边的点比父节点小，右边的点比父节点大。

这里面有提到，平衡的KDTree搜索时效率未必是最优的，为什么

考虑个例子

[[1, 1],
 [2, 1],
 [3, 1],
 [4, 1],
 [5, 1],
 [6, 1],
 [100, 1]，
 [1000, 1]]

这个数据，如果找[100, 1]

搜索KDTree

这部分书中的例子是最近邻的搜索例子。

例子

例3.1

分析p值对最近邻点的影响，这个有一点要注意关于闵可夫斯基距离的理解：

• 两点坐标差的p范数

具体看相关测试案例的实现

例3.2

KDTree创建

例3.3

KDTree搜索

graph TD
	subgraph 对应图3.5
	A[A]---B((B))
	A---C((C))
	B(B)---F((F))
	B---D((D))
	C(C)---G((G))
	C---E((E))
	end

这个例子说明了搜索的方法，理解一下书中的图3.5，对应的KDTree如上。