Earlier, when there was no Internet, each bank had a lot of offices all around Bankopolis, and it caused a lot of problems. Namely, each day the bank had to collect cash from all the offices.
Once Oleg the bank client heard a dialogue of two cash collectors. Each day they traveled through all the departments and offices of the bank following the same route every day. The collectors started from the central department and moved between some departments or between some department and some office using special roads. Finally, they returned to the central department. The total number of departments and offices was n, the total number of roads was n - 1. In other words, the special roads system was a rooted tree in which the root was the central department, the leaves were offices, the internal vertices were departments. The collectors always followed the same route in which the number of roads was minimum possible, that is 2n - 2.
One of the collectors said that the number of offices they visited between their visits to offices a and then b (in the given order) is equal to the number of offices they visited between their visits to offices b and then a (in this order). The other collector said that the number of offices they visited between their visits to offices c and then d (in this order) is equal to the number of offices they visited between their visits to offices d and then c (in this order). The interesting part in this talk was that the shortest path (using special roads only) between any pair of offices among a, b, c and d passed through the central department.
Given the special roads map and the indexes of offices a, b, c and d, determine if the situation described by the collectors was possible, or not.
The first line contains single integer n (5 ≤ n ≤ 5000) — the total number of offices and departments. The departments and offices are numbered from 1 to n, the central office has index 1.
The second line contains four integers a, b, c and d (2 ≤ a, b, c, d ≤ n) — the indexes of the departments mentioned in collector's dialogue. It is guaranteed that these indexes are offices (i.e. leaves of the tree), not departments. It is guaranteed that the shortest path between any pair of these offices passes through the central department.
On the third line n - 1 integers follow: p2, p3, ..., pn (1 ≤ pi < i), where pi denotes that there is a special road between the i-th office or department and the pi-th department.
Please note the joint enumeration of departments and offices.
It is guaranteed that the given graph is a tree. The offices are the leaves, the departments are the internal vertices.
If the situation described by the cash collectors was possible, print "YES". Otherwise, print "NO".
5
2 3 4 5
1 1 1 1
YES
10
3 8 9 10
1 2 2 2 2 2 1 1 1
NO
13
13 12 9 7
1 1 1 1 5 5 2 2 2 3 3 4
YES
In the first example the following collector's route was possible: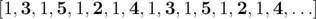 
. We can note that between their visits to offices a and b the collectors visited the same number of offices as between visits to offices b and a; the same holds for c and d (the collectors' route is infinite as they follow it each day).
In the second example there is no route such that between their visits to offices a and b the collectors visited the same number of offices as between visits to offices b and a. Thus, there situation is impossible.
In the third example one of the following routes is: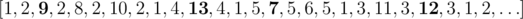 
.
题意概括：给出一棵有根树，四个在根的不同子树中的叶子节点abcd，问有没有一种DFS序使得ab之间的叶子和ab之外的叶子，cd之间的叶子和cd之外的叶子一样多
好题，这一套题的质量都很好。
没想出来，只会做一对点的情况，看了题解。
先考虑一对点的情况，显然这个就是个安排DFS序的问题，而且显然如果叶子节点数是奇数那答案一定是NO，否则设叶子节点数量是k，最终a,b之间的叶子节点数量就是k/2-1。然后问题就变成安排一个DFS顺序使得a,b之间有k/2-1个叶子，很显然的想法是把以每个节点为根的子树里叶子节点的数量统计出来（定义为这个节点的size）。然后考虑1号点的两种子树：
1、不包含a或者b
2、包含a或者b
显然对于第一种子树，要么在a,b之间不包含它，要么整个包含它，因为是DFS序，不能把它拆成两部分
对于第二种子树，把子树的子树分成两种，包含a or b与不包含a or b的，不包含a or b其实是和前面的第一种子树等价的，然后这样递归下去直到最后只剩a or b一个节点
然后就得到了一些互不影响的子树，只要从这些子树里选出一些使得它们的size和是k/2-1，就是简单的背包问题。
然后考虑有两对点的情况，显然这四个点被dfs到的顺序应该是a,c,b,d,a,c,b,d.....或者a,d,b,c,a,d,b,c....这样的形式，因为如果cd在ab同一侧，他们之间的叶子数量一定不到k/2-1，事实上这两种情况是等价的，只需考虑a,c,b,d这种情况即可
这样的话，c所在的子树必然要选，d所在的子树必然不能选，重新做一遍刚才的背包，这次的问题是能否选择一些子树（c和d所在的子树不能选），使得它们的size和是k/2-1-size[c所在的子树]
然后再对cd做一遍，顺序是c,a,d,b，即可，事实上，只要这两个背包分别成立，总可以构造出一个合法的顺序，使得两个背包同时成立，具体方法是，把属于ab不属于cd的放在ac之间，两个都属于的放在cb之间，属于cd不属于ab的放在bd之间即可
考虑一下三对点的情况，ab,cd,ef这个就不好搞了，比如说dfs的顺序是a,c,e,b,d,f，事实上无法构造出一个合理的安排方式是的一个子树属于ab，但是不属于cd,fe，所以好像只能做到两对点
1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define max(a,b) (a>b?a:b) 25 #define min(a,b) (a<b?a:b) 26 #define print_rumtime printf("Running time:%.3lfs ",double(clock())/1000.0); 27 #define TO(j) printf(#j": %d ",j); 28 //#define OJ 29 using namespace std; 30 const int MAXINT = 100010; 31 const int MAXNODE = 5010; 32 const int MAXEDGE = 2 * MAXNODE; 33 char BUF, *buf; 34 int read() { 35 char c = getchar(); int f = 1, x = 0; 36 while (!isdigit(c)) { if (c == '-') f = -1; c = getchar(); } 37 while (isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); } 38 return f * x; 39 } 40 char get_ch() { 41 char c = getchar(); 42 while (!isalpha(c)) c = getchar(); 43 return c; 44 } 45 //------------------- Head Files ----------------------// 46 47 int sz[MAXNODE], cnt, n, a[4], ct[MAXNODE][4], item[MAXNODE], cnt_item, tot, nd; 48 int dp[2][MAXNODE * 2], cnt_s[MAXNODE]; 49 struct edge { 50 int u, v; 51 edge *nxt; 52 edge(int _u, int _v, edge* _nxt) : u(_u), v(_v), nxt(_nxt) {} 53 edge() {} 54 } mp[MAXEDGE], *head[MAXNODE]; 55 void add_edge(int u, int v) { 56 mp[cnt] = edge(u, v, head[u]); 57 head[u] = &mp[cnt++]; 58 mp[cnt] = edge(v, u, head[v]); 59 head[v] = &mp[cnt++]; 60 } 61 void dfs(int p, int fa) { 62 if (!cnt_s[p]) { 63 sz[p] = 1; 64 rep0(i, 4) if (p == a[i]) ct[p][i] = 1; 65 } 66 iter(i, p) { 67 if (i->v == fa) continue; 68 dfs(i->v, p); 69 sz[p] += sz[i->v]; 70 rep0(j, 4) ct[p][j] |= ct[i->v][j]; 71 } 72 } 73 void get_item(int p, int fa, int it) { 74 if (!ct[p][0 ^ it] && !ct[p][1 ^ it]) { 75 item[cnt_item++] = sz[p]; 76 return; 77 } 78 iter(i, p) { 79 if (i->v == fa) continue; 80 get_item(i->v, p, it); 81 } 82 } 83 int bp() { 84 int p = 0; 85 memset(dp, 0, sizeof(dp)); 86 dp[p][0] = 1; 87 dp[p ^ 1][0] = 1; 88 rep0(i, cnt_item) { 89 rep0(j, n) { 90 dp[p ^ 1][j] |= dp[p][j]; 91 dp[p ^ 1][j + item[i]] |= dp[p][j]; 92 } 93 p ^= 1; 94 } 95 return dp[p][nd]; 96 } 97 void get_input(); 98 void work(); 99 int main() { 100 get_input(); 101 work(); 102 return 0; 103 } 104 void work() { 105 dfs(1, 0); 106 if (sz[1] & 1) { 107 printf("NO "); 108 return; 109 } 110 tot = sz[1] / 2 - 1, nd; 111 for (int it = 0; it <= 2; it += 2) { 112 cnt_item = 0; 113 iter(i, 1) { 114 if (ct[i->v][2 ^ it]) { 115 nd = tot - sz[i->v]; 116 continue; 117 } 118 if (ct[i->v][3 ^ it]) continue; 119 if (ct[i->v][0 ^ it] || ct[i->v][1 ^ it]) { 120 get_item(i->v, 1, it); 121 continue; 122 } 123 item[cnt_item++] = sz[i->v]; 124 } 125 if (nd < 0 || !bp()) { 126 printf("NO "); 127 return; 128 } 129 } 130 printf("YES "); 131 } 132 void get_input() { 133 n = read(); 134 rep0(i, 4) a[i] = read(); 135 rep1(i, n - 1) { 136 int v = read(); 137 cnt_s[v]++; 138 add_edge(v, i + 1); 139 } 140 }