1.学习总结(2分)
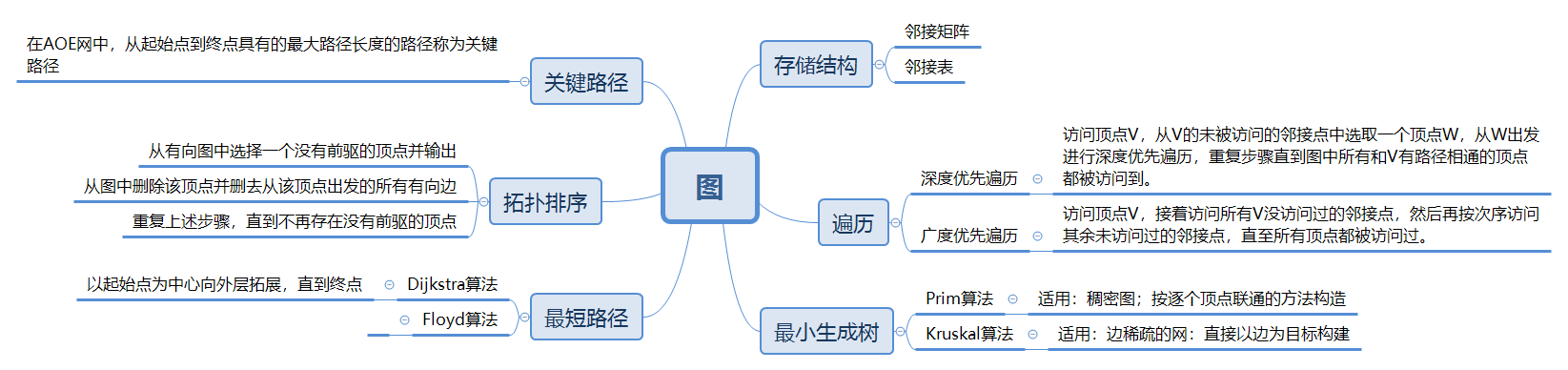
1.1图的思维导图
1.2 图结构学习体会
深度遍历算法:访问顶点V,从V的未被访问的邻接点中选取一个顶点W,从W出发进行深度遍历,重复步骤直到所有和V有相通的顶点都被访问。
广度遍历算法:访问顶点V,接着访问所有V没访问过的邻接点,然后再按次序访问其余未被访问过的邻接点,直至所有顶点都被访问过。
Prim算法:按逐个顶点连通的方法构造。
Kruscal算法:直接以边为目标构建。
Dijkstra算法:以起始点为中心直到终点。
拓扑排序算法:将一个有向无环图进行排序进而得到一个有序的线性序列。
2.PTA实验作业(4分)
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
在mp[501]中输入连接图 color[501]中输入颜色
用s集合判断颜色数量
定义一个判断标准flag=true
如果颜色数量不正确 flag改为false
遍历
如果 i j连接且颜色相同则把flag改为false
最后判断flag是true输出Yes 否则输出No
2.3 代码截图

2.4 PTA提交列表说明。
2.1 题目2:7-2 排座位
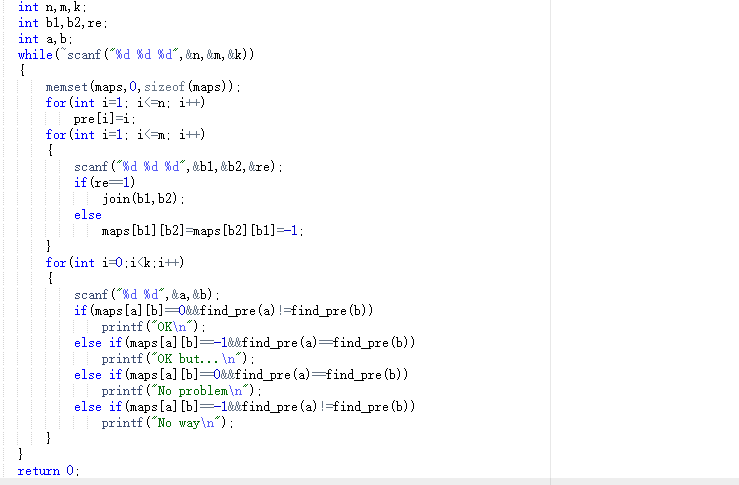
2.2 设计思路(伪代码或流程图)
输入总人数n 总关系数m 查询条数k
输入b1 b2 及他们的关系
输入要查询的宾客a 和b
若他们的maps[a][b]=0且是朋友输出No problem
如果maps[a][b]=0,但不是朋友,则输出OK
如果maps[a][b]=-1,然而也有共同的朋友,则输出OK but...
如果他maps[a][b]=-1且无共同朋友,则输出No way
2.3 代码截图

2.4 PTA提交列表说明。


2.1 题目3:7-3 六度空间
2.2 设计思路(伪代码或流程图)
对每个顶点进行层序遍历(BFS),在遍历过程中,记录顶点所在层数
记录层数利用两个标记变量tail,lastest
tail用于记录当前层的最后一个顶点;在遍历与某个顶点相连的顶点时,lastest用于记录所遍历的当前顶点
当tail == 出队列的顶点时,说明本层已经遍历完毕,则使tail = 当前的lastest,使其等于下一层的最后一个顶点
2.3 代码截图


2.4 PTA提交列表说明。

3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)

3.2 我的总分:225
本题评分规则:
(1)PTA总分310分:3分(全部题目都做)
(2)PTA总分在250分--310分:2.5分(大部分做完1)
(3)PTA总分在200--250分:2分(大部分做完2)
(4)PTA总分在150--200分:1.5分
(5)PTA总分在60分-150分:1分
(6)PTA总分在60分以下:0分
4. 阅读代码(必做,1分)
1.BFS算法求解单源最短路径(BFS总是按照距离由近到远来遍历)
[cpp] view plain copy
#define MAX_VERTEX_NUM 1024
#define INFINITY 0
bool visited[MAX_VERTEX_NUM];
Sequeue Q;
int d[MAX_VERTEX_NUM];
void BFS_MIN_Distance(Graph G,int u){//d[i]表示u到i节点最短路径
for(int i=0;i<G.vexnum;++i)
d[i]=INFINITY;
InitQueue(Q);
visited[u]=TRUE;
EnQueue(Q,u);
while(!isEmpty(Q)){
DeQueue(Q,u);
for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))
if(!visited[w]){
visited[w]=TRUE;
d[w]=d[u]+1;
EnQueue(Q,w);
}
}
}
2.判断图是否是一棵树(是否是连通图)
[cpp] view plain copy
#define MAX_VERTEX_NUM 1024
bool visited[MAX_VERTEX_NUM];
bool IsTree(Graph G){
if(G.vexnum!=G.arcnum-1) //不满足树的性质直接false
return FALSE;
for(int i=0;i<G.vexnum;i++)
visited[i]=FALSE;
DFS(G,0);
for(int i=0;i<G.vexnum;i++)
if(visited[i]==FALSE)
return FALSE; //进行一次DFS有一个孤立点就false
return TRUE;
}
void DFS(Graph G,int v){
visited[v]=TRUE;
for(int w=FirstNeighbor(G,v);w>=0;w=NextNeighor(G,v,w)) //图为邻接矩阵存储
if(!visited[w])
DFS(G,w);
}
3.设图邻接表存储,设计一个算法,输出顶点Vi到顶点Vj所有简单路径
[cpp] view plain copy
#define MAX_VERTEX_NUM 1024
#define INFINITE -65535
bool visited[MAX_VERTEX_NUM];
int path[MAX_VERTEX_NUM];
void PrintAllSimplenessPath(ALGraph G,int From,int To){
for(int i=0;i<G.vexnum;i++)
visited[i]=FALSE;
FindPath(G,From,To,0);
}
void FindPath(ALGraph G,int From,int To,int len){
if(visited[From])
return;
path[len]= From;
visited[u]=TRUE;
if(From==To){
for(int i=0;i<len;i++)
printf(“%d ”path[i]);
visited[From]=FALSE;
return;
}
for(AcrNode *w=G.vertices[From];w;w->next)
FindPath(G,w->next,To,len+1);
visited[From]=FALSE;
}
4.DFS非递归算法(图用邻接表存储)
[cpp] view plain copy
#define MAX_VERTEX_NUM 1024
bool visited[MAX_VERTEX_NUM];
void DFS(ALGraph G){
for(int i=0;i<G.vexnum;i++)
visited[i]=FALSE;
SeqStack S;
for(int i=0;i<G.vexnum;i++){
if(!visited[i]){
Push(S,i);
while(!IsEmpty(S)){
int v=Pop(S);
if(!visited[v]){
visited[v]=TRUE;
printf(“%d ”,v);
for(ArcNode *w=G.vertices[v];w;w=w->next)
if(!visited[w->adjvex])
Push(S,w->adjvex);
}
}
}
}
}
其余还有:
5.设无向图G采用邻接表结构存储,试编写算法计算G中包含的连通分量的数量。
6.在有向图中,我们将入度和出度相等的顶点定义为“平衡顶点”。编写一个算法输出一个采用邻接表存储结构的有向图中所有的平衡顶点。
7.假设图采用邻接表存储,试设计算法判断顶点i和顶点j(i不等于j)之间是否有路径。
8.假设一个连通图采用邻接表作为存储结构,设计一个算法,判断其中是否存在回路。
链接:https://blog.csdn.net/qq78442761/article/details/78824383