插头dp 笔记
限于我的水平,我们暂时只讨论“简单路径问题”,并且例题不多
基础知识
这个东西的全称是 “基于连通性的状态压缩dp”。cdq有一篇论文讲这个,是2008年的论文。
顾名思义,它干的事情其实是,把“连通性”这个东西给压缩起来了,并用这个压缩方式,做一个dp。
插头是啥
我们想要解决选路径的问题。考虑现在有一个图,现在加进来一个点,这个新点和原来的点有一些边。
那选择的路径会发生怎么样的变化呢?对于原来的点,如果它已经有 (2) 的度数,那它就已经在路径上,不能接更多的点了。而那些度数为 (1) 的点,就可以在边上接一个点,这就是一个 “插头”
怎么压缩连通性
对于一般图,显然,我们可以给一个连通块标一个号。但是标号的方法有很多,我们需要找一种可以唯一确定,并且高效的记状态的方法。
这很好搞,我们for一遍当前的点,碰到一个没标号的,就 ++tot。容易发现这样标的方法显然唯一,并且 tot 恰好等于连通块数。标号完之后哈希一波就行了。复杂度是 O(划分数)。如果要求准确,使用map的话,可能要多个log。
有一类特殊问题:要求在网格图上搞一条路径,穿过整个网格。比如说,一条哈密顿路。
这个问题有着一个特殊性,就是我们只需要记一条轮廓线的 (m+1) 个插头,就可以转移。如下图,每次我们讨论一下这条轮廓线“折角”的那个位置的两个头怎么变化就行了。
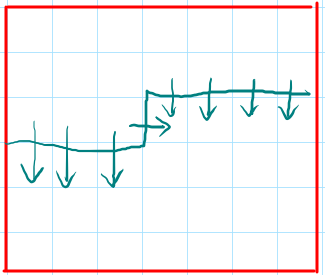
考虑这条轮廓线上的插头的连通性,发现它一定是两两配对,并且不相交的,像括号匹配一样。
为什么?考虑一条穿过整个网格的路径,它肯定会跨过轮廓线,偶数次。一头进,一头出,那么这两个点的连通性就是匹配的。
不相交这个性质,想象一下就知道了,因为相交就会有度数 (>2) 的点。
我们可以把它的状态压缩成:(0/1/2)。对于那些配对的点,我们令左边那个是 (1),右边那个是 (2),就像括号匹配一样。对于没有插头的那些位置,我们给他一个 (0)。
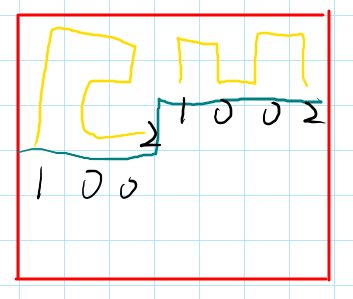
比如上面那个图,假设内部的连接情况如黄线所示,我们就给它一个 (1,0,0,2,1,0,0,2) 的状态。
这可以用三进制存,状态数的数量是 (O(3^{m+1}))。
来个例题
1 Ural 1519 Formula 1 / HNOI2004邮递员
哈密顿回路计数。(n,mle 12)。有障碍。(HNOI那个题没有,不影响本质)
考虑每个格子,四个方向的连接情况,相当于在下面的 (6) 个东西里面选一个

相当于在 (4) 个方向里选两个,({4choose 2}=6)。
状态的表示已经整好了,考虑如何转移。
影响转移的只有“折角”的那两个格子。讨论它们插头有无的情况。
设这两个格子的状态是 (p,q),(p) 在左,(q) 在右。
1. 都没有,p=q=0
那往左,往上的插头都不行,就只能有一种情况,就是往右、下的插头。
然后我们需要把这两个位置的状态从原来的 (p=0,q=0) 变成 (p=1,q=2) ,因为这两个插头正好匹配
2. 其中一个有, pq=0, p+q>0
此时 (p+q) 为 (p,q) 中非 (0) 的那个
那我们的其中一根插头,肯定在左、上里面选,并且得选有插头的那一个。另一根插头,在右、下里面选。
转移到的状态肯定其中一个是 (0),另一个是 (p+q)。
有两种,变成 (0,p+q) 和 (p+q,0)
3. 俩都有
最复杂的情况,此时我们还需要讨论
3.1 两个左/右括号,p=q=1/2
首先是 (p,q) 这两个位置被合并,都变成 (0)
其实是,原来和 (p,q) 匹配的那两个位置,现在也匹配上了,我们依次给它 (1,2)
3.2 右+左,p=2,q=1
原来 (p,q) 匹配的两个位置,现在匹配上了,(p,q) 变成 (0)。
从 (1,2,1,2) 变成 (1,0,0,2)。我们发现,只需要改 (p,q) 俩位置,原来那些就自动匹配上了,根据括号序列的性质。
3.3 左+右,p=1,q=2
此时连接上 (p,q),就会有一个环出来。
而我们哈密顿路要求只有一个环,那一定是做到了最后一个格子,并且除了 (p,q) 位置都是 (0)。那此时会连出来恰好一个环。
这个情况直接转移给答案就行了。
完毕。
此时把代码写出来,发现就按这个讨论的思路把代码实现了就行。(为啥有这么毒瘤的讨论,因为它本来就有这么毒瘤的讨论)
不是我对着代码在瞎讲,是这代码就得对着讨论写
注意到两个细节:
- 换行,此时必须行末没有插头才行。然后我们可以把这个空插头,移到最前面,以方便下一行的转移
- 障碍,这要求折角的两个位置 (p,q) 都是 (0),并转移到 (0,0) 的状态
并小心另一个细节:当上面的两个细节 同时出现 的时候。
(我就因为这个WA了好久)
(这是ural那个题的代码,HNOI那个题的代码要小小的写个高精)
怎么只有一个题啊
会整的会整的,会有更多的qaq