目录
(字符串的匹配)
- 正则化表达式匹配【含通配符】
- 正则化(数字字母)匹配【if re.search('^[0-9a-zA-Z]+$',ss): return True】
- 字符串匹配问题、赎金信(一个字符串字母是不是都在另一个字符串中)
- 同构字符串
- 单词模式
- 查找和替换模式
- 判断字符串A是否包含字符串B【字典实现】
- 重复子字符串
- 判断两个字符串是否互为旋转词
- 判断两个字符串是否互为变形词
- 判断两个字符串是否为换位字符串(python)
- 数组中两个字符串的最小距离【两个位置变量】
- 求字符串的编辑距离(python)【动态规划】
- 两个字符串的最长公共子序列
- 两个字符最长公共子串(python)
- 特殊等价字符串组
- 拼接所有字符串产生字典顺序最小的大写字符串
- 字符串的字典序最长子序列
- 按照给定的字母序列对字符数组排序(python)
- 数组中词典中最长的字符串
- 删除字符串重复的字母,返回字典序最小的一个
- 求两个绝对路径的相对路径(python)
- 如何查找到目标词的最短链长度(python)
- 找到由其他单词组成的最长单词(python)
- 字典树(前缀树)的实现
一、题目:正则化表达式匹配【含通配符】
给定一个正则字符串p,一个字符串s。要求验证s和p是否能匹配。
特别的,正则字符串中仅由两个特殊字符:'.'表示任意的单个字符,'*'表示其前方紧邻元素连续出现0个或者更多个。要求匹配需要覆盖整个输入字符串,而不是部分的匹配。
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
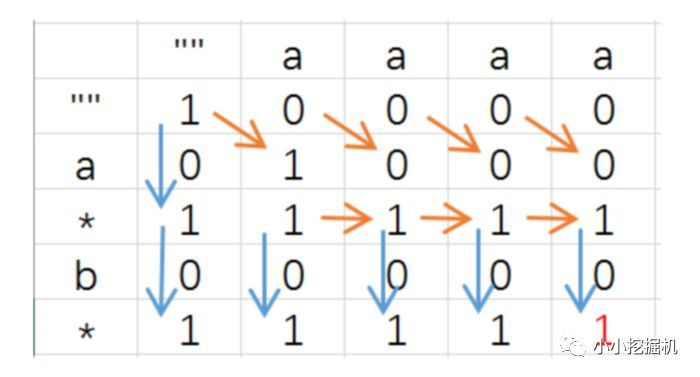
思路:动态规划:
状态转移数组 f [i] [j] 表示利用 p 的前 i 个字符匹配 s 的前 j 个字符的匹配结果(成功为true,失败为false)。
边界:
-
- dp[0][0] = True,s和p都是空格。
- i = 0,只有p为这种情况 p = ‘a*b*c*'才能True,别的都为False。
for i in range(1,len(p)+1):
if p[i-1] == '*': if i >= 2:
dp[0][i] = dp[0][i-2]
-
- j = 0,全部为False。即p为空,都False。
非边界:
如果s[i] == p[j] 或者 p[j] == '.':【如果s的最后一位和p的最后一位相同,则只需要判断前面的】
dp[i][j] = dp[i - 1][j - 1]
如果p[j] == '*':【dp[i][j-2]:*前面一位为0个即可,Sx~P】【dp[i][j-1]:*前面一位为1个,Sx~Pz】【dp[i-1][j]:*匹配x(x==z或者z=='.'), S~Pzy】
dp[i][j] = dp[i][j-2] || dp[i][j-1] || (dp[i-1][j] and (s[i-1]==p[j-2] or p[j-2]=='.'))
解释:
对于s和p,设各个最后一个字符为x, y,p的倒数第二字符为z,除此外前面字符设为S,P,则:
s = Sx
p = Pzy
-
- 如果x == y或y == '.',则如果S和Pz匹配,则s和p匹配,因为最后两字字母是匹配的。这就缩减了问题规模。
- 而对于y == '*'的情况,需要考虑z:
如果x != z,则只有在s和P匹配的情况下,s和p才匹配。
如果x == z,设匹配符号为~吧,方便,则如果S~Pzy,Sx~P,Sx~Pz,【S~P,S~Pz也匹配】都可得出s和p匹配。
代码:
def isMatch(self, s, p):
"""
:type s: str
:type p: str
:rtype: bool
"""
dp = [[False] * (len(p) + 1) for i in range(len(s) + 1)]
dp[0][0] = True
for i in range(1,len(p)+1):
if p[i-1] == '*':
if i >= 2:
dp[0][i] = dp[0][i-2]
for i in range(1,len(s)+1):
for j in range(1,len(p)+1):
if p[j-1]=='.' or s[i-1] == p[j-1]:
dp[i][j] = dp[i-1][j-1]
elif p[j-1]=='*':
dp[i][j] = dp[i][j-2] or dp[i][j-1] or (dp[i-1][j] and (s[i-1]==p[j-2] or p[j-2]=='.'))
return dp[len(s)][len(p)]
一、题目:同构字符串
给定两个字符串 s 和 t,判断它们是否是同构的。
如果 s 中的字符可以被替换得到 t ,那么这两个字符串是同构的。
所有出现的字符都必须用另一个字符替换,同时保留字符的顺序。两个字符不能映射到同一个字符上,但字符可以映射自己本身。
示例 1:
输入: s = "egg", t = "add"
输出: true
示例 2:
输入: s = "foo", t = "bar"
输出: false
示例 3:
输入: s = "paper", t = "title"
输出: true
说明:
你可以假设 s 和 t 具有相同的长度。
代码:
def isIsomorphic(self, s, t):
return len(set(zip(s,t))) == len(set(s)) == len(set(t))
二、题目:单词模式:
给定一种 pattern(模式) 和一个字符串 str ,判断 str 是否遵循相同的模式。
这里的遵循指完全匹配,例如, pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应模式。
示例1:
输入: pattern = "abba", str = "dog cat cat dog"
输出: true
示例 2:
输入:pattern = "abba", str = "dog cat cat fish"
输出: false
示例 3:
输入: pattern = "aaaa", str = "dog cat cat dog"
输出: false
示例 4:
输入: pattern = "abba", str = "dog dog dog dog"
输出: false
说明:
你可以假设 pattern 只包含小写字母, str 包含了由单个空格分隔的小写字母。
代码:
def wordPattern(self, pattern, str):
"""
:type pattern: str
:type str: str
:rtype: bool
"""
a = str.split(" ")
if len(pattern) != len(a):
return False
return len(set(zip(a,pattern))) == len(set(pattern)) == len(set(a))
三、题目:查找和替换模式
你有一个单词列表 words 和一个模式 pattern,你想知道 words 中的哪些单词与模式匹配。
如果存在字母的排列 p ,使得将模式中的每个字母 x 替换为 p(x) 之后,我们就得到了所需的单词,那么单词与模式是匹配的。
(回想一下,字母的排列是从字母到字母的双射:每个字母映射到另一个字母,没有两个字母映射到同一个字母。)
返回 words 中与给定模式匹配的单词列表。
你可以按任何顺序返回答案。
示例:
输入:words = ["abc","deq","mee","aqq","dkd","ccc"], pattern = "abb"
输出:["mee","aqq"]
解释:
"mee" 与模式匹配,因为存在排列 {a -> m, b -> e, ...}。
"ccc" 与模式不匹配,因为 {a -> c, b -> c, ...} 不是排列。
因为 a 和 b 映射到同一个字母。
提示:
1 <= words.length <= 501 <= pattern.length = words[i].length <= 20
思路:时间O(n2)
对每个单词判断其与相应模式是否匹配,匹配则输出。
判断是否匹配函数strMatch,由于题目已知单词长度相同,只需判断在相同的位置,两个单词要有相同的相等或者不等关系即可。
代码:
def findAndReplacePattern(self, words, pattern):
"""
:type words: List[str]
:type pattern: str
:rtype: List[str]
"""
if not words or not pattern:
return []
def isSamePattern(s1,s2):
for i in range(len(s1)):
for j in range(i+1,len(s1)):
if s1[i] == s1[j] and s2[i] != s2[j]:
return False
elif s2[i] == s2[j] and s1[i] != s1[j]:
return False
return True
i = 0
while i < len(words):
if isSamePattern(words[i],pattern):
i += 1
else:
del words[i]
return words
一、重复子字符串
给定一个非空的字符串,判断它是否可以由它的一个子串重复多次构成。给定的字符串只含有小写英文字母,并且长度不超过10000。
示例 1:
输入: "abab" 输出: True 解释: 可由子字符串 "ab" 重复两次构成。
示例 2:
输入: "aba" 输出: False
示例 3:
输入: "abcabcabcabc" 输出: True 解释: 可由子字符串 "abc" 重复四次构成。 (或者子字符串 "abcabc" 重复两次构成。)
代码:
def repeatedSubstringPattern(self, s):
"""
:type s: str
:rtype: bool
"""
if not s:
return False
ss = (s + s)[1:-1]
return ss.find(s)!=-1
二、判断两个字符串是否互为旋转词
如果一个字符串str,把字符串str前面任意的部分挪到后面形成的字符串叫做str的旋转词。
如str="12345",str的旋转词有"12345"、"23451"、"34512"、"45123"、"51234"。
给定两个字符串a和b,请判断a和b是否互为旋转词。
举例:
a="cdab",b="abcd",返回true;
a="1ab2",b="ab12",返回false;
a="2ab1",b="ab12",返回true。
要求:
如果a和b长度不一样,那么a和b必然不互为旋转词,可以直接返回false。
当a和b长度一样,都为N时,要求解法的时间复杂度为O(N)。
思路:
将两个b拼接在一起赋值给c,查看c中是否包含字符串a,若包含,则返回true;否则返回false。
代码:
def isRotation(a,b):
if len(a) != len(b):
return False
c = b+b
return (a in c)
a = 'cdab'
b = 'abcd'
isRotation(a,b)
三、题目:互为变形词
题目:给定两个字符串str1和str2,如果str1和str2中出现的字符种类一样且每种字符出现的次数也一样,则str1和str2互为变形词。
请实现函数判断两个字符串是否互为变形词。
举例:
str1="123", str2="231", 返回true;
str1="123", str2="2331",返回false。
思路:
1. 首先比较两个字符串的长度,长度不同肯定是false。
2. 如果长度相同,新建一个字典,用以存储每个字符出现次数。
3. 遍历str1,在str1 中出现一次就加1,遍历str2,在str2 中出现一次就减1,最后遍历完str2没有出现负值,就返回true。
代码:
from collections import Counter
def IsDeformation(str1,str2):
if not str1 or not str2 or len(str1) != len(str2):
return False
countstr1 = Counter(str1)
for s2 in str2:
if s2 in countstr1:
countstr1[s2] -= 1
if countstr1[s2] < 0:
return False
else:
return False
return True
str1 = '1234'
str2 = '2313'
IsDeformation(str1,str2)
一、数组中两个字符串的最小距离

思路:两个变量分别更新str1和str2的位置,res记录两个变量差的最小值。

代码:
import sys
def minDistance(strs,str1,str2):
if not strs or not str1 or not str2:
return -1
if str1 == str2:
return 0
last1 , last2 , res = -1 , -1 , sys.maxsize
for i in range(len(strs)):
if strs[i] == str1:
if last2 != -1:
res = min(res,i - last2)
last1 = i
if strs[i] == str2:
if last1 != -1:
res = min(res,i - last1)
last2 = i
return res if res != sys.maxsize else -1
strs = ['3','1','3','3','3','2','3','1']
str1 = '1'
str2 = '2'
minDistance(strs,str1,str2)
二、题目:最小编辑代价
给定两个字符串str1和str2,再给定三个整数ic,dc,rc,分别代表插入、删除、替换一个字符的代价,返回将str1编辑成str2的最小代价。
举例:
str1="abc" str2="adc" ic=5 dc=3 rc=2,从"abc"编辑到"adc"把b替换成d代价最小,为2;
str1="abc" str2="adc" ic=5 dc=3 rc=10,从"abc"编辑到"adc",先删除b再插入d代价最小,为8;
思路:动态规划:时间O(M*N),空间O(M*N)
动态规划表:dp[i][j]表示str1[0......i-1]编辑成str2[0......j-1]的最小编辑代价,dp大小为(M+1)*(N+1)是为了从空串开始计算,即dp[0][0]表示空串编辑到空串的最小编辑代价。


- 初始化:
dp[0][0] = 0
dp[0][j] = j * len(s2)
dp[i][0] = i * len(s1)
- dp[i][j] = min( dp[i][j-1]+ic , dc+dp[i-1][j] , dp[i-1][j-1] + rc 【如果str1[i-1]==str2[j-1],rc = rc,否则,rc = 0】)
2.求第一行dp[0][j],空串编辑成str2[0....j-1],则dp[0][j]=ic*j;
3.求第一列dp[i][0],str1[0......i-1]编辑成空串,则dp[i][0]=dc*i;
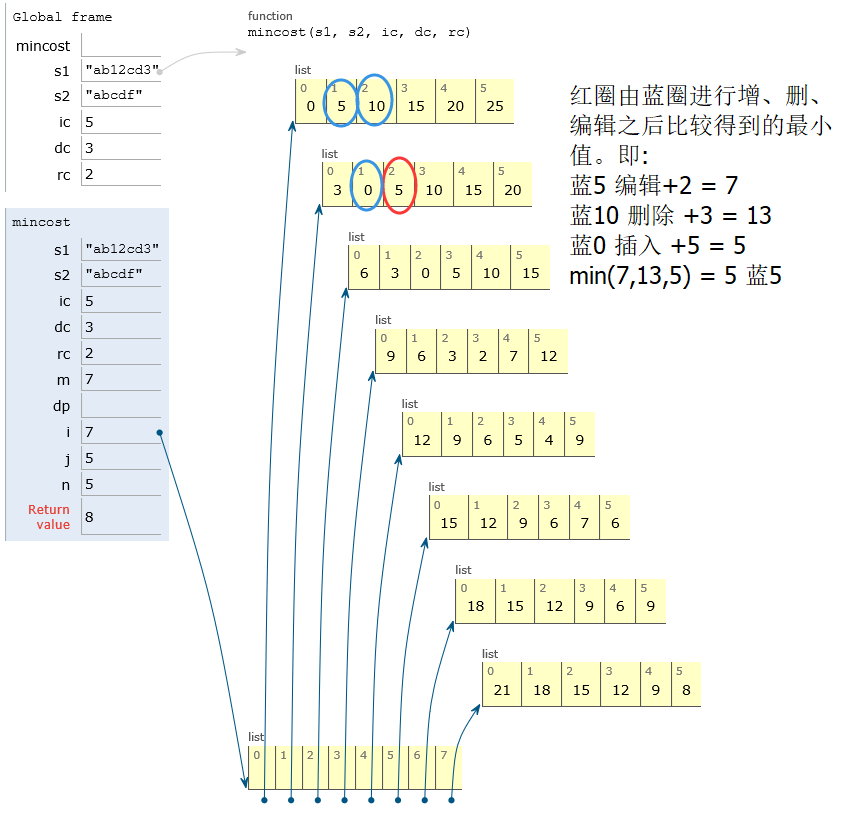
4.求dp[i][j],即str1[0....i-1]编辑成str2[0.....j-1],三种可能的途径:
<1>str1[0....i-1]先编辑成str2[0.....j-2],再由str2[0.....j-2]插入到str2[0.....j-1],即 dp[i][j-1] + ic;
<2>str1[0....i-1]先编辑成str1[0.....i-2],再由str1[0.....i-2]删除到str2[0.....j-1],即 dp[i-1][j] + dc;
<3>如果str1[i-1]==str2[j-1],则 dp[i][j] = dp[i-1][j-1];
如果str1[i-1]!=str2[j-1],则 dp[i][j] = dp[i-1][j-1] + rc;
代码:
def mincost(s1,s2,ic,dc,rc):
m , n = len(s1) , len(s2)
if not s1:
return n*ic
if not s2:
return m*dc
dp = [[0] * (n+1) for i in range(m+1)]
for i in range(1,n + 1):
dp[0][i] = ic * i
for j in range(1,m + 1):
dp[j][0] = dc * j
for i in range(1,m+1):
for j in range(1,n+1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = dp[i-1][j-1] + rc
dp[i][j] = min( dp[i][j] , dp[i-1][j] + dc , dp[i][j-1] + ic)
return dp[-1][-1]
s1 = 'ab12cd3'
s2 = 'abcdf'
ic , dc , rc = 5,3,2
mincost(s1,s2,ic,dc,rc)
三、题目:最长公共子序列:
给定两个字符串,求解这两个字符串的最长公共子序列(Longest Common Sequence)。比如字符串L:BDCABA;字符串S:ABCBDAB
则这两个字符串的最长公共子序列长度为4,最长公共子序列是:BCBA
思路:动态规划:时间O(n * m),空间O(n * m)
创建 DP数组C[i][j]:表示子字符串L【:i】和子字符串S【:j】的最长公共子序列个数。
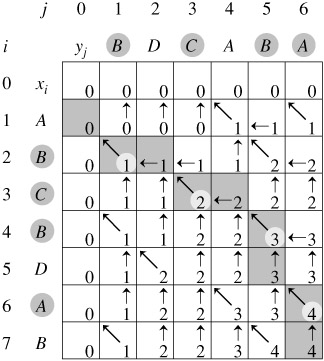
状态方程: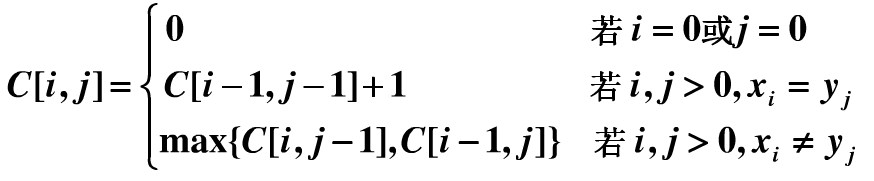
个数代码:
def LCS(L,S):
if not L or not S:
return ""
dp = [[0] * (len(L)+1) for i in range(len(S)+1)]
for i in range(len(S)+1):
for j in range(len(L)+1):
if i == 0 or j == 0:
dp[i][j] = 0
else:
if L[j-1] == S[i-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
return dp[-1][-1]
L = 'BDCABA'
S = 'ABCBDAB'
LCS(L,S)
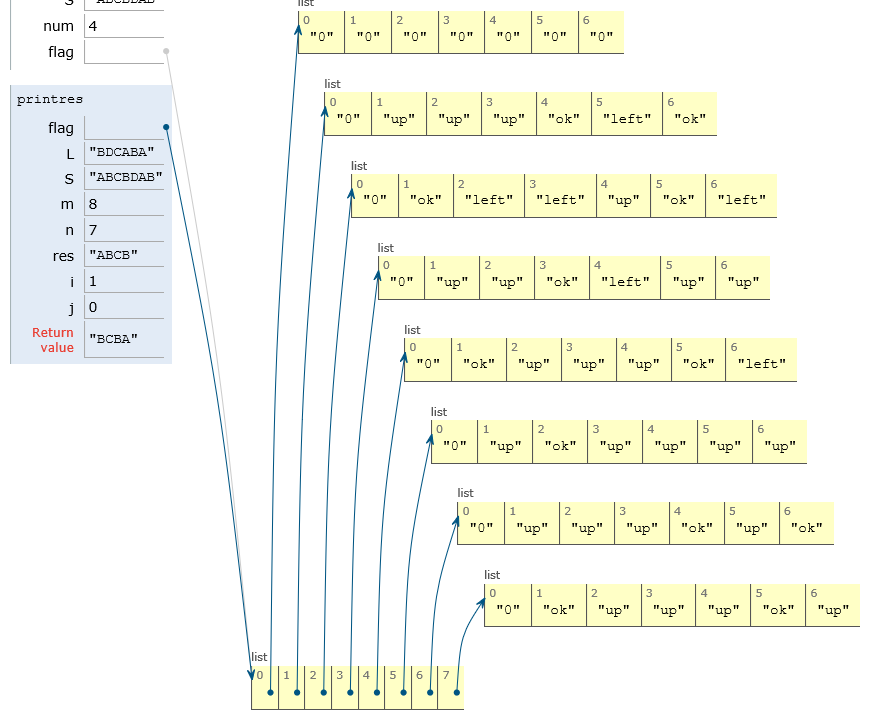
最长子序列代码:设置一个标志
def LCS(L,S):
if not L or not S:
return ""
res = ''
dp = [[0] * (len(L)+1) for i in range(len(S)+1)]
flag = [['left'] * (len(L)+1) for i in range(len(S)+1)]
for i in range(len(S)+1):
for j in range(len(L)+1):
if i == 0 or j == 0:
dp[i][j] = 0
flag [i][j] = '0'
else:
if L[j-1] == S[i-1]:
dp[i][j] = dp[i-1][j-1] + 1
flag[i][j] = 'ok'
else:
dp[i][j] = max(dp[i-1][j],dp[i][j-1])
flag[i][j] = 'up' if dp[i][j] == dp[i-1][j] else 'left'
return dp[-1][-1],flag
def printres(flag,L,S):
m = len(flag)
n = len(flag[0])
res = ''
i , j = m-1 , n-1
while i > 0 and j > 0:
if flag[i][j] == 'ok':
res += L[j-1]
i -= 1
j -= 1
elif flag[i][j] == 'left':
j -= 1
elif flag[i][j] == 'up':
i -= 1
return res[::-1]
L = 'BDCABA'
S = 'ABCBDAB'
num,flag = LCS(L,S)
res = printres(flag,L,S)
四、题目:最长公共子串
找出两个字符串最长连续的公共字符串,如两个母串cnblogs和belong,最长公共子串为lo
思路:动态规划:时间O(N*M),空间O(N*M)
将二维数组c[i][j]用来记录具有这样特点的子串——结尾同时也为子串x1x2⋯xi与y1y2⋯yj的结尾的长度。
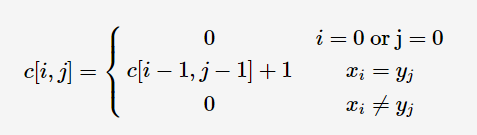
代码:
def lcs(s1,s2):
if not s1 or not s2:
return 0
c = [[0] * len(s2) for i in range(len(s1))]
result = 0
for i in range(len(s1)):
for j in range(len(s2)):
if i == 0 or j == 0:
c[i][j] = 0
else:
if s1[i-1] == s2[j-1]:
c[i][j] = c[i-1][j-1] + 1
result = max(c[i][j],result)
else:
c[i][j] = 0
return result
s1 = 'cnblogs'
s2 ='belong'
lcs(s1,s2)
六、题目:字符串的字典序最长子序列
对于字符串a和b,如果移除字符串a中的一些字母(可以全部移除,也可以一个都不移除)就能够得到字符串b,则b为a的子序列。例如,‘heo'为'hello'的子序列,’le'不是。
对于给定的一个字符串s,请计算出s的字典序最大的子序列。
输入:输入包括一行,一个字符串s,字符串s长度length(1<=length<=50),s中每个字符串都是小写字母
输出:输出字符串,即s的字典序最大的子序列。
例如:‘test'输出:’tt' 'string' 输出 ‘trng' 'bike'输出'ke'
解法1:逆序排序,输出原来的索引值,保留上升的索引值,输出原来字符串对应索引值的子序列。
def Sublist(s):
'''
type(s)=string
'''
value_s=list(s)
key_s=range(len(s))
dic=dict(zip(key_s,value_s))
#字典逆序排序
sort_dic=sorted(dic.items(),key=lambda x:x[1],reverse=True)
key=[]
value=[]
for item in sort_dic:
key.append(item[0])
value.append(item[1])
#获得逆序后的索引值
cur=key[0]
k=0
for i in range(len(key)):
if key[i-k]>=cur:
cur=key[i-k]
else:
del key[i-k]
k+=1
#返回对应索引的原字符串子序列
res=[]
for i in key:
res.append(value_s[i])
return str(res)
解法2:逆向查找字符串,若前面的字符比后面一个大,则保留前面的字符,否则把它删除。
def Subdic(s1):
s=list(s1)
s.reverse()
k=0
for i in range(len(s)-1):
if s[i-k]>s[i+1-k]:
del s[i+1-k]
k+=1
s.reverse()
return str(s)
五、拼接所有字符串产生字典顺序最小的大写字符串

思路:排序本身时间O(NlogN)
假设两个字符分别是a,b。a和b拼起来的字符串表示为a.b,那么如果a.b的字典顺序小于b.a,就把a放在前面,否则把b放在前面。每两两字符之间都按照这个标准进行比较,以此标准排序后,最后串起来的结果就是正确答案。
如 ‘b' , 'ba',’b'和‘ba'排序后,’ba'应与'b'位置交换,‘ba’在前,‘b’在后。
代码:cmp_to_key是因为python3中没有cmp这种用法,取代的。
def lowestString(chas):
if chas == None or len(chas) == 0:
return ""
from functools import cmp_to_key
chas = sorted(chas, key=cmp_to_key(lambda x,y: 1 if x+y > y+x else -1))
return ''.join(chas)
chas = ['b','ba','abc','dba']
lowestString(chas)
七、按照给定的字母序列对字符数组排序(python)

思路1:采用字典存储规则:按照规则两两比较字符串
代码:
1 from functools import cmp_to_key 2 3 4 def camp(s1, s2, dic): 5 m, n = len(s1), len(s2) 6 i, j = 0, 0 7 while i < m and j < n: 8 tmp1, tmp2 = list(s1)[i], list(s2)[j] 9 if tmp1 not in dic: 10 dic[tmp1] = -1 11 if tmp2 not in dic: 12 dic[tmp2] = -1 13 if dic[tmp1] > dic[tmp2]: 14 return 1 15 elif dic[tmp1] < dic[tmp2]: 16 return -1 17 else: 18 i += 1 19 j += 1 20 if i == len1: 21 return 1 22 else: 23 return -1 24 25 26 def compare(arr): 27 dic = {'d': 0, 'g': 1, 'e': 2, 'c': 3, 'f': 4, 'b': 5, 'o': 6, 'a': 7} 28 if len(arr) <= 1: 29 return arr 30 res = sorted(arr, key=cmp_to_key(lambda x, y: camp(x, y, dic))) 31 32 return res 33 34 35 arr = ['bed', 'dog', 'dear', 'eye'] 36 print(compare(arr))
八、题目:词典中最长的子序列
给出一个字符串数组words组成的一本英语词典。从中找出最长的一个单词,该单词是由words词典中其他单词逐步添加一个字母组成。若其中有多个可行的答案,则返回答案中字典序最小的单词。
若无答案,则返回空字符串。
示例 1:
输入: words = ["w","wo","wor","worl", "world"] 输出: "world" 解释: 单词"world"可由"w", "wo", "wor", 和 "worl"添加一个字母组成。
示例 2:
输入: words = ["a", "banana", "app", "appl", "ap", "apply", "apple"] 输出: "apple" 解释: "apply"和"apple"都能由词典中的单词组成。但是"apple"得字典序小于"apply"。
注意:
- 所有输入的字符串都只包含小写字母。
words数组长度范围为[1,1000]。words[i]的长度范围为[1,30]。
2、思路:
排序列表,从后往前遍历排序的列表,再遍历单词的子序列在不在列表中,若全在则把该单词加进结果列表中。最后找出结果列表中最长的单词,若多个单词长度一样,则选择字典序最前的。
代码1:
def longestWord(self, words):
"""
:type words: List[str]
:rtype: str
"""
res=[]
if not words:
return ""
else:
newWords=sorted(words)
for i in range(0,len(newWords)):
last_word=newWords[len(newWords)-1-i]
while last_word in newWords:
last_word=last_word[:-1]
if not last_word:
res.append(newWords[len(newWords)-1-i])
result=sorted(res,key=lambda x:len(x),reverse=True)
flag=0
for i in range(0,len(result)):
if i==len(result)-1 or len(result[i])!=len(result[i+1]):
flag=i
break
else:
continue
return "" if not result else result[i]
代码2:
def longestWord(self, words):
ans = ""
wordset = set(words)
for word in words:
if len(word) > len(ans) or len(word) == len(ans) and word < ans:
if all(word[:k] in wordset for k in range(1, len(word))):
ans = word
return ans
题目:删除字符串重复的字母,返回字典序最小的一个
思路:采用一个栈stack存字母、采用一个count字典数字符串的字符个数、采用一个visited字典表示该字母是否已经确定。
class Solution(object): def removeDuplicateLetters(self, s): """ :type s: str :rtype: str """ count = collections.Counter(s) stack = [] visited = collections.defaultdict(bool) for c in s: count[c] -= 1 if visited[c]: continue while stack and count[stack[-1]] and stack[-1] > c: visited[stack[-1]] = False stack.pop() visited[c] = True stack.append(c) return "".join(stack)
