1、综述
scikit-learn的线性回归模型都是通过最小化成本函数来计算参数的,通过矩阵乘法和求逆运算来计算参数。当变量很多的时候计算量会非常大,因此我们改用梯度下降法,批量梯度下降法每次迭代都用所有样本,快速收敛但性能不高,随机梯度下降法每次用一个样本调整参数,逐渐逼近,效率高,本节我们来利用随机梯度下降法做拟合。
2、随机梯度下降法
梯度下降就好比从一个凹凸不平的山顶快速下到山脚下,每一步都会根据当前的坡度来找一个能最快下来的方向。随机梯度下降英文是Stochastic gradient descend(SGD),在scikit-learn中叫做SGDRegressor。
3、样本实验
代码:

1 from sklearn.linear_model import SGDRegressor 2 from sklearn.preprocessing import StandardScaler 3 import matplotlib.pyplot as plt 4 5 plt.figure()#实例化作图变量 6 plt.title('single variable') 7 plt.xlabel('x') 8 plt.ylabel('y') 9 plt.grid(True) 10 plt.plot(X, y, 'k.') 11 #plt.show() 12 13 X_scaler = StandardScaler() 14 y_scaler = StandardScaler() 15 X = [[50],[100],[150],[200],[250],[300]] 16 y = [[150],[200],[250],[280],[310],[330]] 17 X = X_scaler.fit_transform(X) #用什么方法标准化数据? 18 y = y_scaler.fit_transform(y) 19 X_test = [[40],[400]] # 用来做最终效果测试 20 X_test = X_scaler.transform(X_test) 21 22 model = SGDRegressor() 23 model.fit(X, y.ravel()) 24 y_result = model.predict(X_test) 25 plt.plot(X_test, y_result) 26 plt.show()
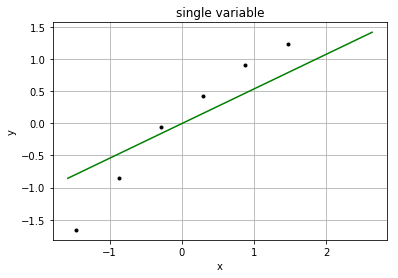
结果:

这里需要用StandardScaler来对样本数据做正规化,同时对测试数据也要做正规化。
我们发现拟合出的直线和样本之间还是有一定偏差的,这是因为随机梯度是随着样本数量的增加不断逼近最优解的,也就是样本数量越多就越准确。
优化
既然样本数多拟合的好,那么我们把已有的样本重复多次试一下,修改成如下:
1 X = [[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300]] 2 y = [[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],
代码:

1 from sklearn.linear_model import SGDRegressor 2 from sklearn.preprocessing import StandardScaler 3 import matplotlib.pyplot as plt 4 5 plt.figure()#实例化作图变量 6 plt.title('single variable') 7 plt.xlabel('x') 8 plt.ylabel('y') 9 plt.grid(True) 10 plt.plot(X, y, 'k.') 11 X_scaler = StandardScaler() 12 y_scaler = StandardScaler() 13 #X = [[50],[100],[150],[200],[250],[300]] 14 #y = [[150],[200],[250],[280],[310],[330]] 15 X = [[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300],[50],[100],[150],[200],[250],[300]] 16 y = [[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330],[150],[200],[250],[280],[310],[330]] 17 #plt.show() 18 X = X_scaler.fit_transform(X) #用什么方法标准化数据? 19 y = y_scaler.fit_transform(y) 20 X_test = [[40],[400]] # 用来做最终效果测试 21 X_test = X_scaler.transform(X_test) 22 23 model = SGDRegressor() 24 model.fit(X, y.ravel()) 25 y_result = model.predict(X_test) 26 plt.plot(X_test, y_result, 'g-') 27 plt.show()
结果: