参考:https://blog.csdn.net/niepangu/article/details/45499383
计算CRC的过程,就是用一个特殊的“除法”,来得到余数,这个余数就是CRC。
它不是真正的算术上的除法!过程和算术除法过程一样,只是加减运算变成了XOR(异或)运算!
算术上的除法:
120÷9=13 余 3,120是被除数,9是除数,13是商,3是余数。念作120除以9,或者9除120,或
者9去除120!(除法的过程就不写了)
这个除法计算机当然会做,但是做起来很麻烦,因为减法有借位,很耗时间和指令!
所以,计算CRC也是除法,但是用XOR来代替减法,这就简单多了!
CRC的除法:
120÷9=14 余 6,商、余数和算术除法不一定相同!!因为除法用的是XOR,而不是真正的减法。
以二进制模拟这个计算过程:
120 二进制:1111000 、除数9 二进制:1001 、商 14 二进制:1110 余数6 二进制:110
从高位1111开始,每次进行一次XOR 的到的值后,去掉最高位加入下一位,每加一次进行一次XOR运算。
1111
^1001
--------------
0110
第一次XOR后得到0110,去掉最高位0,加入下一位0, 得1100 ,这样最高位是1,所以下个商是1 ,用^1001【很明显保留的位数与1001 保持一致】
1100
^1001
--------------
0101
第二次XOR ,去掉最高位,加入下一位0,得1010 ,这样最高位是1,所以下个商是1 ,用^1001
1010
^ 1001
---------------
0011
第三次XOR,去掉最高位,加入下一位0,得0110 ,这样最高位是1,所以下个商是0 ,用^0000
0110
^ 0000
-------------
0110
最后一次XOR后得到0110,最高位的0可以消掉了,得到余数为110,即6
注意,余数不是0110,而是110,因为最前面那个0已经被XOR后消掉了!
可见,除法(XOR)的目的是逐步消掉最高位的1或0!
由于过程是XOR的,所以商是没有意义的,我们不要。我们要的是余数。
余数110是1111000的CRC吗?不是!
余数110是1111(即十进制15)的CRC!!!
为什么?因为CRC是和数据一起传送的,所以数据后面要加上CRC。
数据1111加上CRC110后,变成1111110,再传送。接收机收到1111110后,除以除数1001,余数为
000,正确;如果余数不为0,则说明传送的数据有误!这样完成CRC校验。
即发送端要发送1111,先在1111后加000,变成1111000,再除以1001得到余数110,这个110
就是CRC,将110加到数据后面,变成1111110,发送出去。
接收端收到1111110,用它除以1001,计算得余数为000,就说明收到的数据正确。
所以原始数据后面要先扩展出3位0,以容纳CRC值!
会发现,在上面的除法过程中,这3位0,能保证所有的4个数据位在除法时都能够被处理到!不然做
一次除法就到结果了,那是不对的。这个概念后面要用到。
二、 生成项
上面例子中,生成项是1001,共4位比特,最高位的1,实际上在除法的每次XOR时,都要消掉,所
以这个1可不做参考,后3位001才是最重要的!001有3位,所以得到的余数也是3位,因为最后一次除
法XOR时,最高位消掉了。所以CRC就是3位比特的。
CRC是3比特,表示它的宽度W=3。也就是说,原始数据后面要加上W=3比特的0进行扩展!
生成项的最低位也必须是1,这是规定的。
生成项1001,就等效于g(x)=x2+1
生成项也可以倒过来写,即颠倒过来,写成1001,这里倒过来的值是一样的。
再如CRC32的生成项是:
1 0000 0100 1100 0001 0001 1101 1011 0111 (33个比特)
即g(x)= x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1
颠倒过来,就可以写成1110 1101 1011 1000 1000 0011 0010 0000 1
一般生成项简写时不写最高位的1,故生成项是0x04C11DB7,颠倒后的生成项是0xEDB88320
CRC32的生成项是33比特,最高位是消掉的,即CRC值是32比特(4个字节),即宽度W=32,就是说,
在计算前,原始数据后面要先扩展W=32个比特0,即4个0x00字节。
注意:我看到网上CRC32的POLY有0x04C10DB7这个值的,它和正规的POLY值不同,需要注意!
颠倒过来,即是镜像,为什么要颠倒,后述。
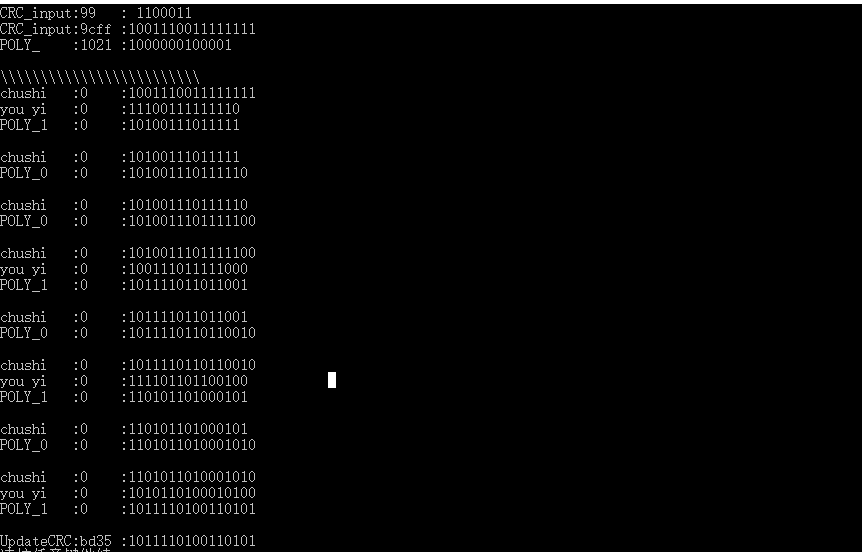
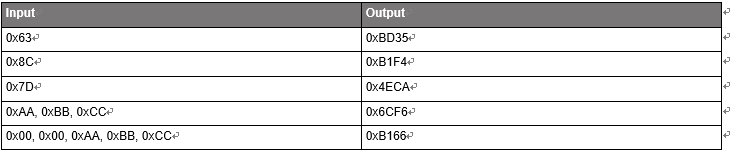
拿运 CRC CCITT-16 为例子,行下面的代码,CRC_acc = 0xFFFF;CRC_input[0] = 0x63; 返回校验值CRC.
unsigned short UpdateCRC(unsigned short CRC_acc, unsigned char *CRC_input, unsigned int len)
{
unsigned char i,k = 0;
#define POLY_ 0x1021
while (len--)
{
CRC_acc = CRC_acc ^ (CRC_input[k++] << 8);
printf("CRC_input:%d : %s
", CRC_input[0], itoa(CRC_input[0], binbuf, 2));
printf("CRC_input:%x :%s
", CRC_acc, itoa(CRC_acc, binbuf, 2));
printf("POLY_ :%x :%s
", POLY_, itoa(POLY_, binbuf, 2));
printf("\\\\\\\\\\\\\\\\\\\\\\\\\
");
for (i = 0; i < 8; i++)
{
if ((CRC_acc & 0x8000) == 0x8000)
{
printf("chushi :%x :%s
", 0, itoa(CRC_acc, binbuf, 2));
CRC_acc = CRC_acc << 1;
printf("you yi :%x :%s
", 0, itoa(CRC_acc, binbuf, 2));
CRC_acc ^= POLY_;
printf("POLY_1 :%x :%s
", 0, itoa(CRC_acc, binbuf, 2));
}
else
{
printf("chushi :%x :%s
", 0, itoa(CRC_acc, binbuf, 2));
CRC_acc = CRC_acc << 1;
printf("POLY_0 :%x :%s
", 0, itoa(CRC_acc, binbuf, 2));
}
}
}
return CRC_acc;
}