本篇博客基本全篇转自https://www.cnblogs.com/staginner/archive/2012/08/13/2636826.html,太强啦ORZ
题意
A是个1*n的矩阵,每个元素是1或者0,你需要构造一个矩阵A,使得D=(A*B-C)*AT最大,其中B是个给出的n*n的矩阵,C是个给出的1*n的矩阵,他们的元素都是非负的。输出最大的D。
分析
从本质上讲,之所以能够用最大流解决这个问题,关键在于最大流可以求解下面这个函数的最小值:
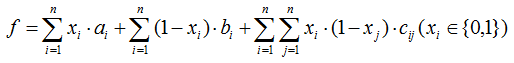
接下来就分析一下如何用最大流求解上面这个函数的极值。
首先xi一共只有两种选择,那么最终可以按xi的取值将xi划分成两个集合,那么如果xi在值为1的集合里,xj在值为0的集合里,那么就会产生一个代价cij。同时如果xi选择0就会产生一个bi的代价,如果xi选择1就会产生一个ai的代价。
于是构造一个源点S,汇点T做最小割,不妨假设做完最小割之后值为1的xi的集合是和S相连的部分,值为0的xi的集合是和T相连的部分。
由于表达式中有三项,我们用三种割边来分别描述这三项的值。一种是xi选择了1,这样就不能选择0,需要把xi-T这条边割掉,由于xi选择1会产生ai的代价,那么就把这条边的容量设为ai。另一种是xi选择了0,这样就不能选择1,需要把S-xi这条边割掉,由于xi选择0会产生bi的代价,那么就把这条边的容量设为bi。最后一种是xi选择了1,xj选择了0,这样xi和xj不能在同一个集合中,需要把xi-xj这条边割掉,由于xi选择1,xj选择0产生cij的代价,那么就把这条边的容量设为cij。
这样对建好的图做最小割就可以得到上面哪个函数的最小值。
-----------------------------------------------------------------------我是分割线--------------------------------------------------------------------------------------------------
然后我们回归原题,想办法朝上面的式子方向进行转化。
本题的计算写出来是这个样子的

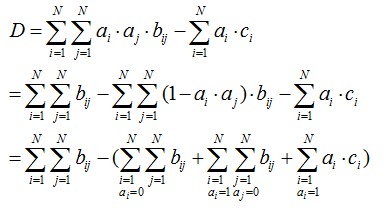
然后就可以按照上面的方法通过网络流来求解这个题。