P3515 [POI2011]Lightning Conductor

传送门

设 $f[i]$ 表示题目要求的 $p$

那么有 $f[i]=max(f[j]+sqrt {left | i-j ight |})$，考虑去掉绝对值

$f[i]=max(a[j]+sqrt {i-j}),j<=i$，$f[i]=max(a[j]+sqrt {j-i}),i<j$

后面一半和前面一半是一样的，考虑先求出前面一半，然后再和后面取 $max$

前面一半单次转移是 $O(n)$ 的，猜一下这种方程有单调性

即如果 $i$ 的最优决策点为 $k$ ，那么 $j>i$ 的最优决策点 $l$ 一定大于等于 $k$

考虑证明：

假设不单调

那么有 $f[i]=a[k]+ sqrt {i-k}>=a[l]+ sqrt {i-l}$

并且有 $f[j]=a[l]+ sqrt {j-l}>=a[k]+ sqrt {j-k}$

上面的不等式可以变成 $a[k]-a[l]>=sqrt {i-l}-sqrt {i-k}$

下面的不等式可以变成 $a[k]-a[l]<=sqrt {j-l}-sqrt {j-k}$

和起来说明 $sqrt {i-l}-sqrt {i-k}<=sqrt {j-l}-sqrt {j-k}$

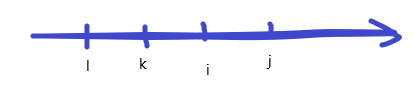
考虑 $i,j,k,l$ 在数轴上的位置，如图：

并考虑上式在图像 $y=sqrt x$ 下的样子

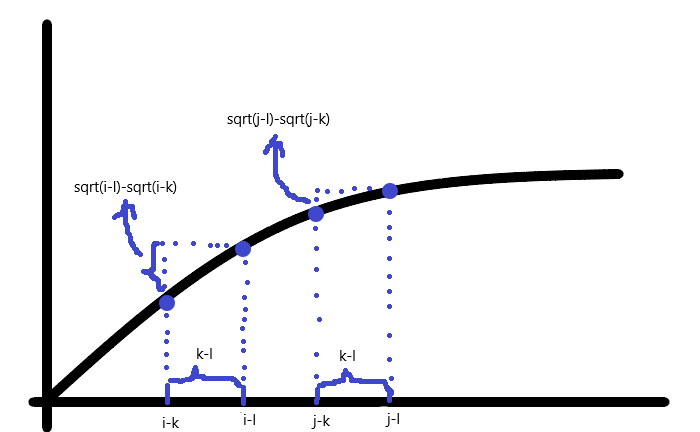
由图显然 $sqrt {i-l}-sqrt {i-k}>sqrt {j-l}-sqrt {j-k}$

所以矛盾，即转移单调

然后考虑维护每个位置的最优转移点，发现我们只要记录最优转移点之间的边界和转移点的编号

这个搞个单调栈维护，更新 $f$ 时在单调栈上找到相应区间，更新边界时用二分即可

具体看代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
typedef double db;
inline int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
    return x*f;
}
const int N=1e6+7;
int n,a[N];
int pos[N],Q[N];
db f[N],sqr[N];//注意double
inline db calc(int i,int j) { return 1.0*a[j]+sqr[i-j]-a[i]; }//计算dp值
inline int find(int x,int y)//二分出转移点x,y之间的边界
{
    int l=y,r=n,mid,res=l-1;
    while(l<=r)
    {
        mid=l+r>>1;
        if(calc(mid,x)>calc(mid,y)) l=mid+1,res=mid;
        else r=mid-1;
    }
    return res;
}
void work()
{
    int l=1,r=0; memset(pos,0,sizeof(pos));
    for(int i=1;i<=n;i++)
    {
        while(l<r && pos[l]<i ) l++;//找到控制i的区间
        f[i]=max(f[i],calc(i,Q[l]));
        while(l<r && calc(pos[r-1],Q[r])<calc(pos[r-1],i)) r--;//把不优的区间去掉
        pos[r]=find(Q[r],i); Q[++r]=i;
    }
}
int main()
{
    n=read(); for(int i=1;i<=n;i++) a[i]=read(),sqr[i]=sqrt(i);
    work(); reverse(a+1,a+n+1); reverse(f+1,f+n+1);/*记得f也要翻转*/ work();
    for(int i=n;i;i--) printf("%d
",max((int)ceil(f[i]),0));
    return 0;
}