题解P4917 天守阁的地板

题目：P4917 天守阁的地板  

双倍经验：P5221 Product  

先说这题怎么做。

首先我们知道可以铺的地板块数为lcm(a,b)*lcm(a,b)/(a*b)=a*b/gcd(a,b)*lcm(a,b)/(a*b）=lcm(a,b)/gcd(a,b)

然后就可以愉快的莫反了。博主惨兮兮不会用LaTeX写数学公式，所以。。搬了一张图。

原文章 因为这位大佬和我的做法很相似，所以借用了他的题解表达出我的想法。

于是我开开心心地做了一下，十分暴力地对于每个n求一遍，喜提60分的佳绩。。。

但我把这份代码改了一下交到P5221 Product，拿到了满分。

#include<stdio.h>
#define it register int
#define il inline
const int mod=104857601;
const int N=1000005;
typedef long long ll;
int n,mu[N],p[N/10+2],cnt;
bool isp[N];
ll ans;
il void mui(){
    mu[1]=1;
    register long long x;
    for(it i=2;i<N;++i){
        if(!isp[i]) p[++cnt]=i,mu[i]=-1;
        for(it j=1;(x=1ll*i*p[j])<N&&j<=cnt;++j){
            isp[x]=1;
            if(!(i%p[j])) break;
            mu[x]=-mu[i];
        }
    }
    for(it i=2;i<N;++i) mu[i]+=mu[i-1];
}
il void ksm(ll x,it l,ll &now){
    now=1;
    while(l){
        if(l&1) now=1ll*now*x%mod;
        x=x*x%mod,l>>=1;
    }
}
il void cal(it x,ll &now){
    now=0;for(it l=1,r;l<=x;l=r+1) r=x/(x/l),now=(now+1ll*(x/l)*(x/l)%(mod-1)*(mu[r]-mu[l-1]+mod-1)%(mod-1))%(mod-1);
}
int main(){
    scanf("%d",&n),mui();ans=1;
    for(it i=2;i<=n;++i) ans=ans*i%mod;
    ksm(ans,n<<1,ans);
    ll now1=0,now2=0,s1=1,s2=1,now3=0;
    it i=1,j=1;
    for(it l=1,r;l<=n;l=r+1){
        r=n/(n/l);
        while(i<=l-1) s1=s1*i%mod,++i;
        while(j<=r) s2=s2*j%mod,++j;
        ksm(s2,mod-2,now2),cal(n/l,now3),ksm(now2*s1%mod,2*now3,now2),ans=ans*now2%mod; 
    }
    printf("%lld",ans); 
    return 0;
}

思考了一下，如果对于每个n求一遍，O(T*n)不超时就怪了。。

那么怎么办呢？最好是可以预处理，然后在sqrt(n)时间内完成

我们再看一眼分母，发现分母可以再化简化简：

 

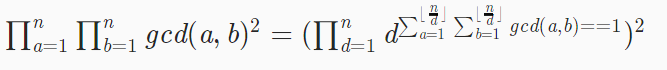
我们可以枚举gcd，然后把式子化简成这样：

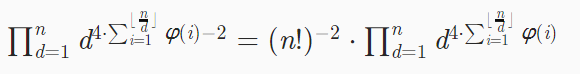
分子分母都有(n!)，把分子里的提上去。于是就可以愉快滴敲代码啦。

#include<stdio.h>
#define it register int
#define il inline
const int N=1000005;
const int mod=19260817;
typedef long long ll;
int mu[N],p[N],T,cnt,n;
bool isp[N];
ll ans,fac[N],o[N],ph[N];
il void ksm(ll x,ll l,ll &now){
    now=1;
    while(l){
        if(l&1) now=now*x%mod;
        x=x*x%mod,l>>=1;
    }
}
il void cal(it x,ll &now){
    now=0;for(it l=1,r;l<=x;l=r+1) r=x/(x/l),now=(now+1ll*(x/l)*(x/l)*(mu[r]-mu[l-1]+mod-1)%(mod-1))%(mod-1);
}
il void phi(){
    ph[1]=1;
    register long long x;
    for(it i=2;i<N;++i){
        if(!isp[i]) ph[i]=i-1,p[++cnt]=i;
        for(it j=1;(x=1ll*i*p[j])<N&&j<=cnt;++j){
            isp[x]=1;
            if(!(i%p[j])) {ph[x]=1ll*ph[i]*p[j];break;}
            ph[x]=1ll*ph[i]*ph[p[j]];
        }
    }
    for(it i=2;i<N;++i) ph[i]=(ph[i]+ph[i-1])%(mod-1);            
}
namespace io {
    const int SIZE = (1 << 21) + 1;
    char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55];
    int f, qr;
#define gc() (iS == iT ? (iT = (iS = ibuf) + fread (ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS ++)) : *iS ++)
    inline void flush () {fwrite (obuf, 1, oS - obuf, stdout);oS = obuf;}
    template <class I>
    inline void fr (I &x) {
        for (f = 1, c = gc(); c < '0' || c > '9'; c = gc()) if (c == '-') f = -1;
        for (x = 0; c <= '9' && c >= '0'; c = gc()) x = x * 10 + (c & 15);
        x *= f;
    }
    struct Flusher_ {~Flusher_() {flush();}} io_flusher_;
}
using io :: fr; 
int main(){     
    phi();
    fr(T);
    fac[0]=fac[1]=1;for(it i=2;i<=1000000;++i) fac[i]=1ll*fac[i-1]*i%mod; 
    ll now1,now2;
    while(T--){
        fr(n);
        ans=1;
        for(it l=1,r;l<=n;l=r+1){
            r=n/(n/l),ksm(fac[l-1],mod-2,now1),ksm(fac[r]*now1%mod,ph[n/l]%mod,now2),ans=ans*now2%mod; 
        } 
        ksm(fac[n],(n<<1|1)+1,now1),ksm(ans,mod-5,ans);//ans^4的逆元  
        printf("%lld
",ans*now1%mod);
    }
    return 0;
}