后缀数组SA
基本信息
sa[i]表示将所有后缀排序后第i小的后缀的编号
rk[i]表示后缀i的排名
sa[rk[i]]=i=rk[sa[i]]
求sa(nlogn)

1 inv get_SA() { 2 for (rint i=1; i<=n; ++i) ++c[x[i]=s[i]]; 3 //c数组是桶 4 //x[i]是第i个元素的第一关键字 5 for (rint i=2; i<=m; ++i) c[i]+=c[i-1]; 6 //做c的前缀和,我们就可以得出每个关键字最多是在第几名 7 for (rint i=n; i>=1; --i) sa[c[x[i]]--]=i; 8 for (rint k=1; k<=n; k<<=1) { 9 rint num=0; 10 for (rint i=n-k+1; i<=n; ++i) y[++num]=i; 11 //y[i]表示第二关键字排名为i的数,第一关键字的位置 12 //第n-k+1到第n位是没有第二关键字的 所以排名在最前面 13 for (rint i=1; i<=n; ++i) if (sa[i]>k) y[++num]=sa[i]-k; 14 //排名为i的数 在数组中是否在第k位以后 15 //如果满足(sa[i]>k) 那么它可以作为别人的第二关键字,就把它的第一关键字的位置添加进y就行了 16 //所以i枚举的是第二关键字的排名,第二关键字靠前的先入队 17 for (rint i=1; i<=m; ++i) c[i]=0; 18 //初始化c桶 19 for (rint i=1; i<=n; ++i) ++c[x[i]]; 20 //因为上一次循环已经算出了这次的第一关键字 所以直接加就行了 21 for (rint i=2; i<=m; ++i) c[i]+=c[i-1]; //第一关键字排名为1~i的数有多少个 22 for (rint i=n; i>=1; --i) sa[c[x[y[i]]]--]=y[i],y[i]=0; 23 //因为y的顺序是按照第二关键字的顺序来排的 24 //第二关键字靠后的,在同一个第一关键字桶中排名越靠后 25 //基数排序 26 swap(x,y); 27 //这里不用想太多,因为要生成新的x时要用到旧的,就把旧的复制下来,没别的意思 28 x[sa[1]]=1; 29 num=1; 30 for (rint i=2; i<=n; ++i) 31 x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k]) ? num : ++num; 32 //因为sa[i]已经排好序了,所以可以按排名枚举,生成下一次的第一关键字 33 if (num==n) break; 34 m=num; 35 //这里就不用那个122了,因为都有新的编号了 36 } 37 for (rint i=1; i<=n; ++i) printf("%d ",sa[i]); 38 printf(" "); 39 for(int i=1;i<=n;i++) printf("%d ",x[i]); 40 }
寻找最小的循环移动位置
将字符串S复制一份变成SS之后后缀排序
在字符串中找字串
从字符串首尾取字符最小化字典序
每次从首或尾取一个字符组成字符串,问所有能够组成的最小字符串
height数组
基本信息
LCP(最长公共前缀)
lcp(i,j)表示后缀i和后缀j的最长公共前缀
height[i]=lcp(sa[i],sa[i-1]); //第i名的后缀与它前一名的后缀的最长公共前缀
height[rk[i]]>=height[rk[i-1]]+1;
求height数组

1 void hei() 2 { 3 for(int i=1,k=0;i<=n;i++) 4 { 5 if(k) k--; 6 while(s[i+k]==s[sa[x[i]-1]+k]) ++k; 7 height[x[i]]=k; 8 } 9 }
两个字串最长公共前缀
lcp(sa[i],sa[j])=min{ height[i+1...j] }
比较一个字符串的两个字串的大小关系
不同字串数目
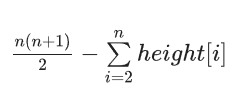
出现至少k次的子串的最大长度
出现k次意味着后缀排序后有至少连续k个后缀的lcp是这个子串
求出每相邻k-1个height的最小值,再求这些最小值的最大值就是答案。
