【核心算法4】广度优先遍历算法

广度优先遍历与深度优先遍历类似，也是查询的方法之一，他也是从某个状态出发查询可以到达的所有状态。

但不同与深度优先遍历，广度优先遍历总是先去查询距离初始状态最近的状态。

• 选课的智慧：如何确定选课的顺序
• 寻找制高点：寻找制高点，抢占有利地形
• 合法的括号：从非法括号中寻找合法括号序列
• 数的右侧： 从树的侧边观察数的伟岸身躯

对比深度优先遍历算法，广度优先遍历算法在搜索所有答案的时候是采用由近及远的方式。先访问离起始点最近的点，再访问远一些的点，就好像先访问走一步可以到达的点，再访问走两步可以到达的点。

因此，广度优先遍历算法也叫做层次遍历算法，一层一层去找问题的答案。

选课的智慧

新学期，将要学习计算机基础、数学、英语、Python、算法等五门课程。其中学习算法之前要先学习Python和英语，在学习Python之前要学习数学和计算机基础

问题求解

广度优先遍历以队列为基础

1. 开始选课时，只能选择没有先修课的科目。比如数学，在选择计算机基础，这样就可以学习Python。为了找出没有先修课的科目，需要建立一个数组来记录每门课的先修课数量，将每门的先修课数量初始化为0，课程数量为num_courses
2. 接下来，需要通过先修课的二维数组pre_list来计算每门课的先修课数量
3. 接下来，建立一个队列queue 存储目前可以选择的课程。将那些先修课数量为0的课程加入队列queue
4. 综上，建立存放每门可曾先修数量的数组pre_list_count 和存放目前可以选修课程的队列queu。
5. 最后使用广度优先遍历开始选课

代码实现

def bfs(num_courses, pre_list):
    # 初始化每门课的先修课数量 0
    pre_list_count = [0]*num_courses
    for line in pre_list:
        for i in range(len(line)):
            if line[i] == 1:
                pre_list_count[i] += 1

    queue = []
    for i in range(len(pre_list_count)):
        # 挑选先修课数量为0 的课程
        if pre_list_count[i] == 0:
            queue.append(i)

    class_task = []
    while len(queue) != 0:
        this_class = queue[0]
        del queue[0]
        class_task.append(this_class)

        for i in range(num_courses):
            if pre_list[this_class][i] == 1:
                pre_list_count[i] -= 1
                # 若一门课的先修课为0，就将其加入队列
                if pre_list_count[i] == 0:
                    queue.append(i)

    return class_task

# 课程与课程之间的依赖关系
pre_list = [
       # M, C, P, E, A
        [0, 0, 1, 0, 0],
        [0, 0, 1, 0, 0],
        [0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1],
        [0, 0, 0, 0, 1],
       ]

class_map = {
    '0': 'Math',
    '1': 'Computer',
    '2': 'Python',
    '3': 'English',
    '4': 'Arithmetic',
}

class_task = bfs(5, pre_list)
for i in class_task:
    print(class_map[str(i)])

寻找制高点

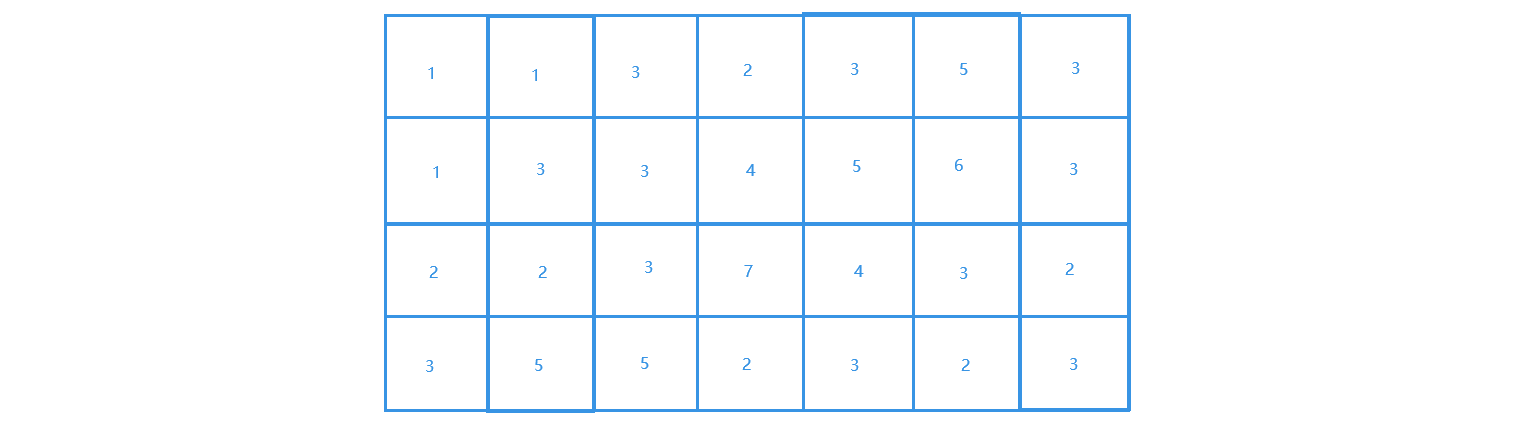
拿到一张海拔图，上面有每个地理位置的海拔高度数据。为了描述这张图，使用同样一个M*N的二维数组表示

如图：

问题求解

若是从每个点出发来搜索是否能达到四个边缘，但不像迷宫问题，搜索的目标点不是单一的，而是所有边缘点，那么这种算法思路显然效率低下。

那么，如何优化算法呢？换个角度思考，以边缘作为起点向内部开始遍历搜索，看下一个节点的高低是否高于或者等于自身的高度，然后标记能够到达的点为True，继续搜索，直到不能走为止。

按照同样的思路分别标记从四个边缘出发可以到达的点，那么最终四者均为True，那，这个点就是我们寻找的制高点。

逆向思维方式很重要

1. 标记地图上的每一个点，定义左上角为(0, 0), 右下角为(m-1, n-1)

2. 首先，根据已知的数据(地图)，也就是一个二维数组。代码框架

   # matrix 是存储地图的二维数组
   def solve(matrix):
       if not matrix:
           return matrix
       # 相应逻辑
   

3. 为了更好的表示可以移动的方向，使用一个二维数组存储上下左右四个方向

   dir = [
       [0, 1], # x坐标+0，y坐标+1，即向下移动
       [0, -1],
       [1, 0],
       [-1, 0]
   ]
   

4. 定义用来存储二维数组大小的变量

5. 开始寻找制高点，队列是完成广度优先遍历必备的数据结构。所以，先把第一行的点全部放入队列，然后开始广度遍历

代码实现

def bfs(set, m, n, matrix):
    dir = [[0, 1], [0, -1], [1, 0], [-1, 0]]
    # list()函数创建queue 为set的队列版本
    queue = list(set)

    while len(queue) > 0:
        # 取出队列的头元素(x, y)
        x, y = queue.pop()
        # 循环遍历四个方向
        for d in dir:
            nx = x + d[0]
            ny = y + d[1]
            # 如果新的点在二维数组中
            if 0 <= nx and nx < m and 0 <= ny and ny < n:
                # 如果新的点原来点高
                if matrix[nx][ny] >= matrix[x][y]:
                    if (nx, ny) not in set:
                        queue.append((nx, ny))
                        set.add((nx, ny))


def solve(matrix):
    if not matrix:
        return matrix

    # 二维数组有多少行
    m = len(matrix)
    # 二维数组有多少列
    n = len(matrix[0])

    top_point = set([(0, y) for y in range(n)])
    left_point = set([(x, 0) for x in range(m)])
    bottom_point = set([(m-1, y) for y in range(n)])
    right_point = set([(x, n-1) for x in range(m)])

    bfs(top_point, m, n, matrix)
    bfs(left_point, m, n, matrix)
    bfs(bottom_point, m, n, matrix)
    bfs(right_point, m, n, matrix)

    res = top_point & left_point & bottom_point & right_point
    result = max(res)
    print('XY:', result)
    comm_height = matrix[result[0]][result[1]]
    return comm_height

matrix = [
    [1, 1, 3, 2, 3, 5, 3],
    [1, 3, 3, 4, 5, 6, 3],
    [2, 2, 3, 7, 4, 3, 2],
    [3, 5, 5, 2, 3, 2, 3]
]

s = solve(matrix)
print(s)

合法的括号

一段代码中充满了括号，为了更快的修改括号匹配问题，可以编写一段代码，来寻找正确的小括号组合。

即在给定的输入字符串中，移除掉最少量的错误括号，从而使得这个字符串变成有效的字符串，并返回

问题求解

1. 对于括号匹配问题，最先想到的应该是栈来解决。常规操作就是遇到左括号的时候入栈，遇见有括号的时候出栈。而对于最短路径，广度优先遍历算法不仅可以找到合法的字符串，还可以找到经过最少变化就能得到合法字符串，所以广度优先遍历算法更适合解决。

2. 首先，解决什么样的字符串是合法的字符串，为了判断一个字符串是否合法。可以使用一个变量来模拟栈，从头到尾扫描，只要遇到左括号就让变量加1，遇到右括号让变量减1，在这个过程中，某一步使得变量的值小于0， 就说明该字符串是一个非法字符串，如果全部都通过的话，就说明它是一个合法的字符串。相比较传统的栈，能更节省内存

   def isvalid(str):
       count = 0
       for i in str:
           if i == '(':
               count += 1
           elif i == ')':
               count -= 1
               if count < 0:
                   return False
       return count == 0
   

3. 将初始字符串加入队列，每次从队列中取出一个字符串，查看它是不是合法的，如果是，则把它加入结果集，返回结果就好，如果不是，遍历这个字符串，只要遇到左右括号字符的时候，就去掉该括号字符生成新的字符串，把它加入到队列中进行分析。对于括号数量为N的字符串，理论上，这一步要产生N-1个字符串，当然还要去除重复的数据，可能会小于N-1个字符串。可以放入一个哈希集合中，减少重复计算

4. 找出所有合法的结果需要一直找到队列为空。如果发现合法的字符串，就不需要继续搜索下去，直接跳出循环，使用该技术称之为剪枝

5. 对队列中的每个字符串都进行相同的操作，还有一种情况是知道队列为空还没找到合法的字符串，就返回空集合。

6. 最后使用广度优先遍历算法对队列进行分析，分析完不是删除，而是留下来做数据处理。

代码实现

def isvalid(str):
    ''' 有效字符串'''
    # 记录括号的数量
    count = 0
    for i in str:
        if i == '(':
            count += 1
        elif i == ')':
            count -= 1
            if count < 0:
                return False
    if count != 0:
        return False
    return True

def bfs(string):
    # 存放最终结果
    res = []
    # 初始字符串加入队列
    queue = [string]

    # 队列不为空是开始进行广度优先遍历
    while len(queue) > 0:
        for i in range(len(queue)):
            if isvalid(queue[i]):
                # 收集合法字符串到结果集中
                res.append(queue[i])

        if len(res) > 0:
            # 合法字符串去重
            return list(set(res))

        # 临时结果集
        temp = []
        # 取出队列中每一个字符串
        for i in queue:
            # 对于每个字符串，分别查看每个字符
            for j in range(len(i)):
                # 如果为左右括号则生成新的字符串，并加入临时结果集
                if i[j] == '(' or i[j] == ')':
                    temp.append(i[: j] + i[j+1: ])

        queue = list(set(temp))
    return list(set(res))

s = '(a)(b))('

print(bfs(s))
### >>>
"""
['(a)(b)', '(a(b))']
"""