线段树

线段树的概念

可以发现，每个叶子结点的值就是原数组的值，每个非叶子结点的度都为二，且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。（概念讲解以区间最值版为例，如果时区间和版，每个父亲的存储的值也就是两个孩子存储的值的和）

线段树的实现方式

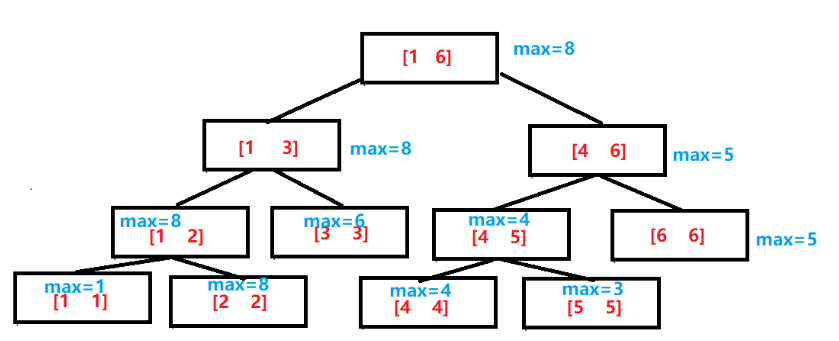
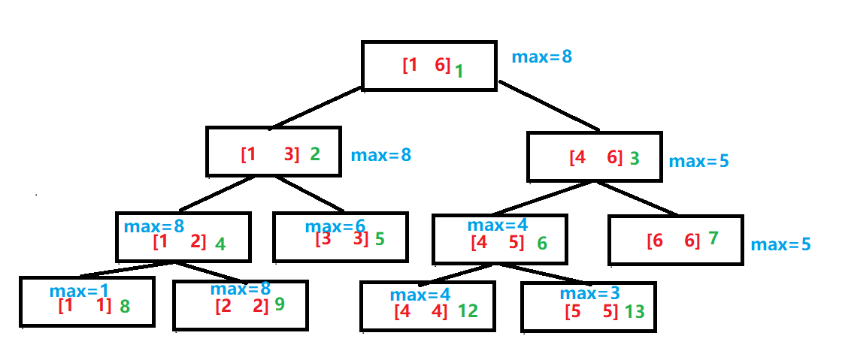
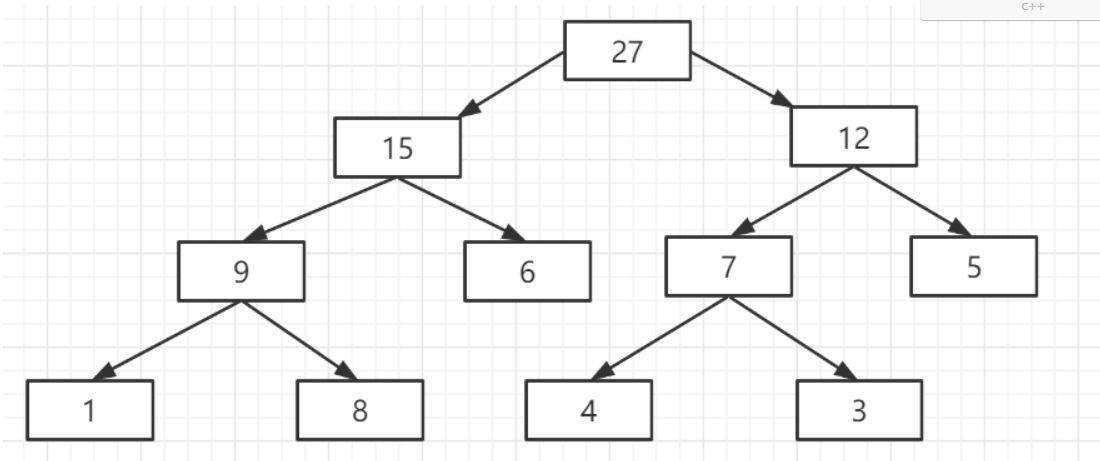
线段树的实现方式之一就是使用数组的方式，用2*i表示第i个节点的左子树，2 * i+1表示第i个节点的右子树。其中绿色的数字就是数组的下标。

相对于树状数组：这里的原数组A[] = {0,1,8,6,4,3,5}；线段树数组c[] = {0 8 8 5 4 5 6 7 8 9 0 0 12 13}（二叉树的层序遍历）数组数据的记录从1开始（后序讲解都使用该例子）

一般线段树数组大小为原数组的4倍

基于求区间最值的线段树

线段树的建立

void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = (l + r) / 2;
        build(2*k, l, m);//不是的话就递归
        build(2*k+1, m + 1, r);
        c[k] = max(c[k * 2], c[k * 2 + 1]);//由于不是最后的叶子节点，所以一定有左右子节点，所以此节点的值就是左右子节点较大的值
    }
}

左移右移版：

void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = l+((r-l)>>1);//注意这里的括号，进行优先级的处理
        build(k<<1, l, m);//不是的话就递归
        build(k<<1|1, m + 1, r);
        c[k] = max(c[k<<1], c[k<<1|1]);//由于不是最后的叶子节点，所以一定有左右子节点，所以此节点的值就是左右子节点较大的值
    }
}

线段树的单点更新

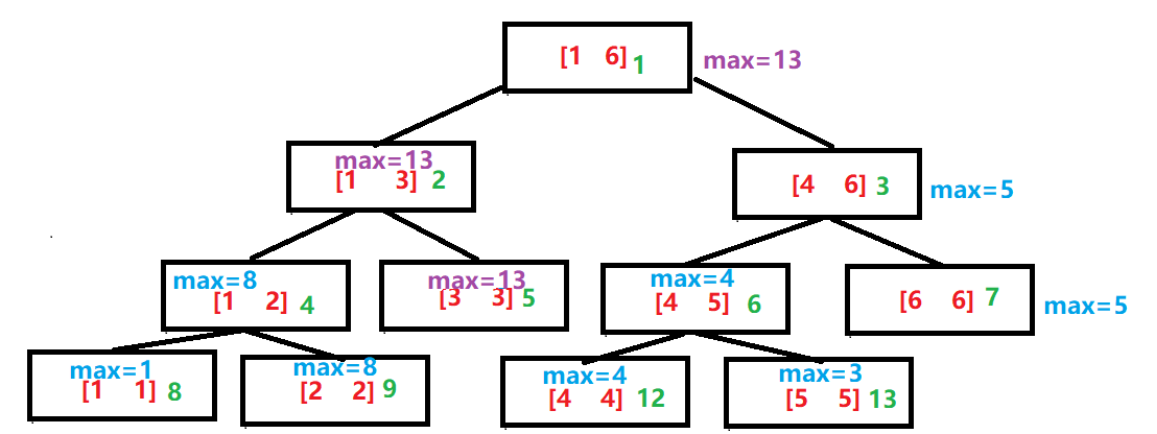
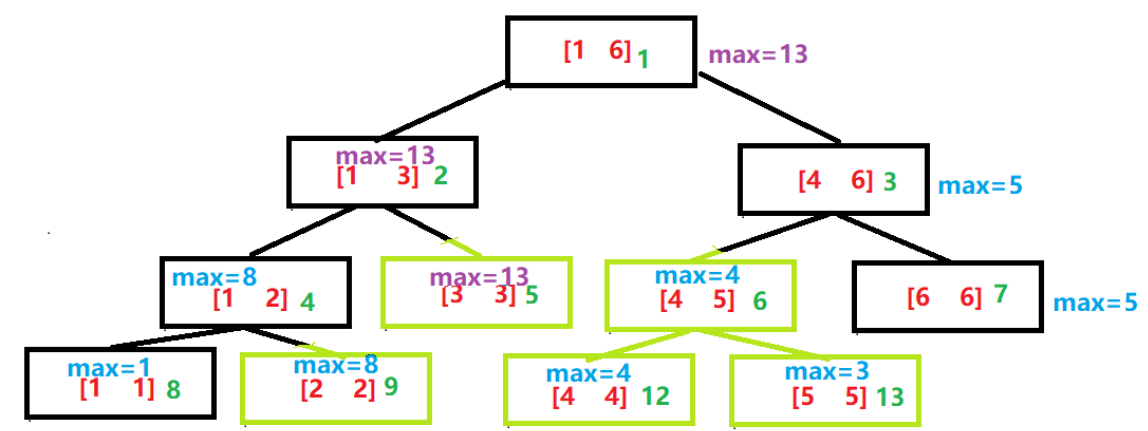
如图：若给原数组a[3]+7，紫色为需要更新的数据

void update(int index,int v,int l,int r,int k) //index为下标，v为要加上的值，
{
    if (l == r)//左端点等于右端点，即为叶子结点，直接加上v即可
    {
        a[l] += v; c[k] += v;//原数组和线段树数组都得到更新
    }
    else
    {
        int m = l + ((r - l) >> 1);//m则为中间点，左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
        if (index <= m)//如果需要更新的结点在左子树区间
            update(index, v, l, m, k<<1);
        else //如果需要更新的结点在右子树区间
            update(index, v, m + 1, r, k<<1|1);
        c[k] = max(c[k << 1], c[k << 1 | 1]);//更新父节点的值
    }
}

线段树的区间查询

比如现在我要查询[2,5]区间的最值，一共有5个区间，而且我们可以发现[4,5]这个区间已经包含了两个子树的信息，所以我们需要查询的区间只有三个，分别是[2,2],[3,3],[4,5]

int query(int L,int R,int l,int r,int k)//[L,R]即为要查询的区间，l，r为结点区间，k为结点下标
{
    if (L <= l&&R >= r) //如果当前结点的区间真包含于要查询的区间内，则返回结点信息且不需要往下递归
        return c[k];
    else
    {
        int res = -INF;
        int m = l + ((r - l) >> 1);//m则为中间点，左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
        if (L <= m)res = max(res, query(L, R, l, m, k << 1));//如果左子树和需要查询的区间交集非空
        if (m < R)res = max(res, query(L, R, m + 1, r, k << 1 | 1));//如果右子树和需要查询的区间交集非空，注意这里不是else if，因为查询区间可能同时和左右区间都有交集
        return res;//返回当前结点得到的信息
    }
}

代码汇总

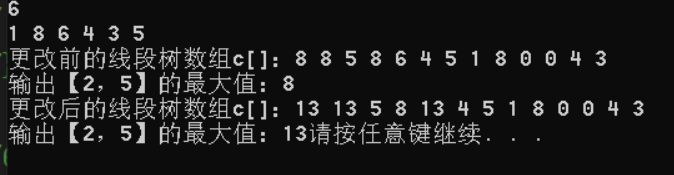
//6
//1 8 6 4 3 5
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 100
#define INF 0x3f3f3f3f
int a[MAX], c[MAX <<2];//空间，一般会开到4*n的空间防止RE。
void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = l+((r-l)>>1);//注意这里的括号，进行优先级的处理
        build(k<<1, l, m);//不是的话就递归
        build(k<<1|1, m + 1, r);
        c[k] = max(c[k<<1], c[k<<1|1]);//由于不是最后的叶子节点，所以一定有左右子节点，所以此节点的值就是左右子节点较大的值
    }
}

void update(int index,int v,int l,int r,int k)
{
    if (l == r)
    {
        a[l] += v; c[k] += v;
    }
    else
    {
        int m = l + ((r - l) >> 1);
        if (index <= m)
            update(index, v, l, m, k<<1);
        else
            update(index, v, m + 1, r, k<<1|1);
        c[k] = max(c[k << 1], c[k << 1 | 1]);
    }
}
int query(int L,int R,int l,int r,int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        int res = -INF;
        int m = l + ((r - l) >> 1);
        if (L <= m)res = max(res, query(L, R, l, m, k << 1));
        if (m < R)res = max(res, query(L, R, m + 1, r, k << 1 | 1));
        return res;
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    build(1, 1, n);
    printf("更改前的线段树数组c[]：");
    for (int i = 1; i <= (n<<1|1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的最大值：");
    printf("%d", query(2, 5, 1, n, 1));
    update(3, 7, 1, n, 1);
    printf("
");
    printf("更改后的线段树数组c[]：");
    for (int i = 1; i <= (n << 1|1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的最大值：");
    printf("%d", query(2,5,1,n,1));
}

线段树的区间更新

线段树的区间更新引进了懒惰标记的概念

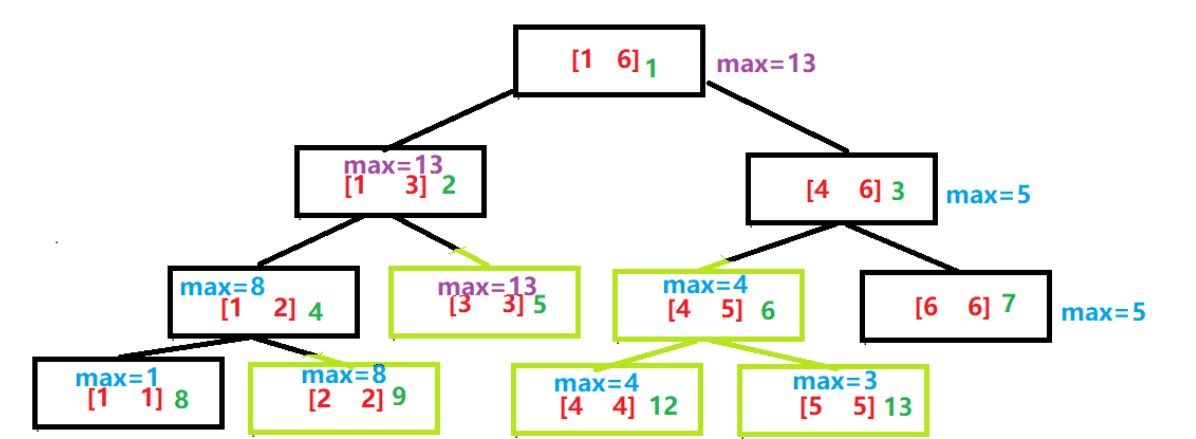
正常的区间更新，比如下图中【2，5】都要+1，则a[2] a[3] a[4] a[5] 都要加 1，则在下图中需要更新很多节点，为了提高更新的效率，每次更新只更新到更新区间完全覆盖线段树结点区间为止

所以标记的含义：本区间已经被更新过了，但是子区间却没有被更新过

void pushdown(int k)
{
    if (lazy[k])//如果有lazy标记
    {
        lazy[k << 1] += lazy[k];//更新左子树的lazy值
        lazy[k << 1|1] += lazy[k];//更新右子树的lazy值
        c[k << 1] += lazy[k];//左子树的最值加上lazy值
        c[k << 1 | 1]+=lazy[k];  //右子树的最值加上lazy值
        lazy[k] = 0;//lazy值归0
    }
}
void update(int L,int R, int v, int l, int r, int k)
{
    if (L <= l&&R >= r) //如果当前结点的区间真包含于要更新的区间内
    {
        lazy[k] += v; //懒惰标记
        c[k] += v; //最大值加上v之后，此区间的最大值也肯定是加v
    }
    else
    {
        pushdown(k);//查询lazy标记，更新子树
        int m = l + ((r - l) >> 1);
        if (L <= m)
            update(L, R, v, l, m,k<<1);
        if (R > m)
            update(L, R, v, m + 1, r, k << 1 | 1);
        c[k] = max(c[k << 1], c[k << 1 | 1]);
    }
    
}

线段树的区间查询

int query(int L,int R,int l,int r,int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        pushdown(k); /*每次都需要更新子树的Lazy标记*/
        int res = -INF;
        int m = l + ((r - l) >> 1);
        if (L <= m)res = max(res, query(L, R, l, m, k << 1));
        if (m < R)res = max(res, query(L, R, m + 1, r, k << 1 | 1));
        return res;
    }
}

代码汇总

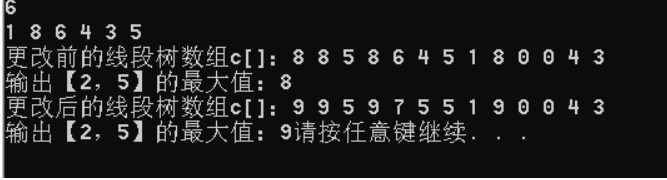
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 100
#define INF 0x3f3f3f3f
int a[MAX], c[MAX << 2], lazy[MAX << 2];//空间，一般会开到4*n的空间防止RE。
void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = l + ((r - l) >> 1);//注意这里的括号，进行优先级的处理
        build(k << 1, l, m);//不是的话就递归
        build(k << 1 | 1, m + 1, r);
        c[k] = max(c[k << 1], c[k << 1 | 1]);//由于不是最后的叶子节点，所以一定有左右子节点，所以此节点的值就是左右子节点较大的值
    }
}

void pushdown(int k)
{
    if (lazy[k])
    {
        lazy[k << 1] += lazy[k];
        lazy[k << 1|1] += lazy[k];
        c[k << 1] += lazy[k];
        c[k << 1 | 1]+=lazy[k];
        lazy[k] = 0;
    }
}
void update(int L,int R, int v, int l, int r, int k)
{
    if (L <= l&&R >= r)
    {
        lazy[k] += v;
        c[k] += v;
    }
    else
    {
        pushdown(k);
        int m = l + ((r - l) >> 1);
        if (L <= m)
            update(L, R, v, l, m,k<<1);
        if (R > m)
            update(L, R, v, m + 1, r, k << 1 | 1);
        c[k] = max(c[k << 1], c[k << 1 | 1]);
    }
    
}
int query(int L,int R,int l,int r,int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        pushdown(k); /**每次都需要更新子树的Lazy标记*/
        int res = -INF;
        int m = l + ((r - l) >> 1);
        if (L <= m)res = max(res, query(L, R, l, m, k << 1));
        if (m < R)res = max(res, query(L, R, m + 1, r, k << 1 | 1));
        return res;
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    build(1, 1, n);
    printf("更改前的线段树数组c[]：");
    for (int i = 1; i <= (n << 1 | 1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的最大值：");
    printf("%d", query(2, 5, 1, n, 1));
    update(2, 5,1, 1, n, 1);
    printf("
");
    printf("更改后的线段树数组c[]：");
    for (int i = 1; i <= (n << 1 | 1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的最大值：");
    printf("%d", query(2, 5, 1, n, 1));
}

基于求区间和的线段树

线段树的建立

void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = l + ((r - l) >> 1);//注意这里的括号，进行优先级的处理
        build(k << 1, l, m);//不是的话就递归
        build(k << 1 | 1, m + 1, r);
        c[k] = c[k << 1]+c[k << 1 | 1];//这里改为相加
    }
}

线段树的单点更新

void update(int index, int v, int l, int r, int k)
{
    if (l == r)
    {
        a[l] += v; c[k] += v;
    }
    else
    {
        int m = l + ((r - l) >> 1);
        if (index <= m)
            update(index, v, l, m, k << 1);
        else
            update(index, v, m + 1, r, k << 1 | 1);
        c[k] = c[k << 1]+ c[k << 1 | 1];//这里变为相加
    }
}

线段树的区间查询

int query(int L, int R, int l, int r, int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        int res = 0;//这里
        int m = l + ((r - l) >> 1);
        if (L <= m)res +=  query(L, R, l, m, k << 1);//这里
        if (m < R)res += query(L, R, m + 1, r, k << 1 | 1);//这里
        return res;
    }
}

代码汇总

#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 100
#define INF 0x3f3f3f3f
int a[MAX], c[MAX << 2];//空间，一般会开到4*n的空间防止RE。
void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = l + ((r - l) >> 1);//注意这里的括号，进行优先级的处理
        build(k << 1, l, m);//不是的话就递归
        build(k << 1 | 1, m + 1, r);
        c[k] = c[k << 1]+c[k << 1 | 1];//由于不是最后的叶子节点，所以一定有左右子节点，所以此节点的值就是左右子节点较大的值
    }
}

void update(int index, int v, int l, int r, int k)
{
    if (l == r)
    {
        a[l] += v; c[k] += v;
    }
    else
    {
        int m = l + ((r - l) >> 1);
        if (index <= m)
            update(index, v, l, m, k << 1);
        else
            update(index, v, m + 1, r, k << 1 | 1);
        c[k] = c[k << 1]+ c[k << 1 | 1];
    }
}
int query(int L, int R, int l, int r, int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        int res = 0;
        int m = l + ((r - l) >> 1);
        if (L <= m)res +=  query(L, R, l, m, k << 1);
        if (m < R)res += query(L, R, m + 1, r, k << 1 | 1);
        return res;
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    build(1, 1, n);
    printf("更改前的线段树数组c[]：");
    for (int i = 1; i <= (n << 1 | 1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的和：");
    printf("%d", query(2, 5, 1, n, 1));
    update(3, 7, 1, n, 1);
    printf("
");
    printf("更改后的线段树数组c[]：");
    for (int i = 1; i <= (n << 1 | 1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的和：");
    printf("%d", query(2, 5, 1, n, 1));
}

线段树的区间更新

void pushdown(int k,int l,int r)
{
    if (lazy[k])
    {
        int m = (l + r) >> 1;
        lazy[k << 1] += lazy[k];
        lazy[k << 1 | 1] += lazy[k];
        c[k << 1] += lazy[k]*(m-l+1);//注意这里
        c[k << 1 | 1] += lazy[k]*(r-(m+1)+1);//注意这里
        lazy[k] = 0;
    }
}
void update(int L, int R, int v, int l, int r, int k)
{
    if (L <= l&&R >= r)//如果被操作区间完全包含，就不用往下更新了
    {
        c[k] +=(r-l+1)* v;//注意这里
        lazy[k] += v;
    }
    else
    {
        pushdown(k,l,r);
        int m = l + ((r - l) >> 1);
        if (L <= m)
            update(L, R, v, l, m, k << 1);
        if (R >m)
            update(L, R, v, m + 1, r, k << 1 | 1);
        c[k] = c[k << 1]+ c[k << 1 | 1];
    }

}

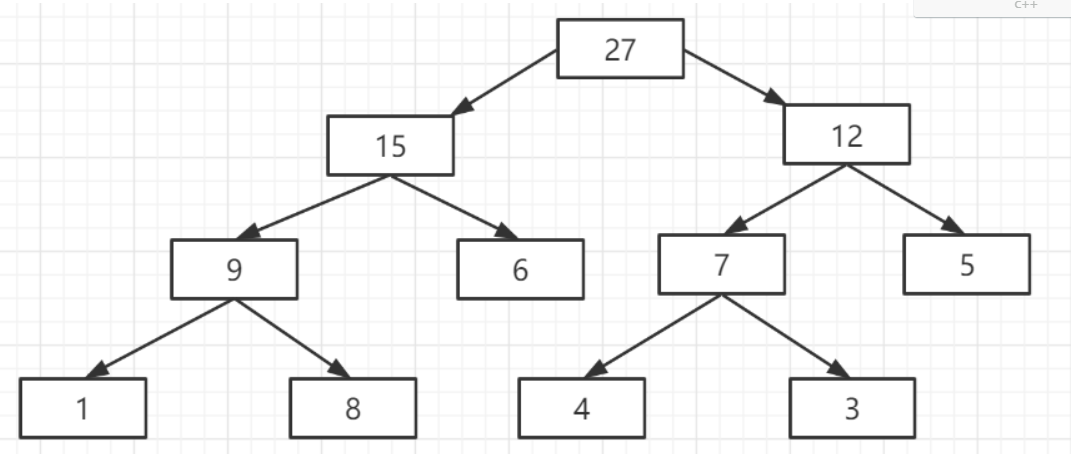
该区间更新如果对原数组的【2，5】依次加一：

应该是这样，但其实不是的，结果其实是这样的：

原因是这样的：

当递归到初始右边节点7的时候已经满足if (L <= l&&R >= r)，即当前结点的区间真包含于要更新的区间内，所以此时直接c[k] +=(r-l+1)* v;计算好节点7下面的子节点个数，一个节点+v，总共就要加(r-l+1)* v，所以节点3 4 就不用加一更新了。

这里求区间和与求区间最值有点小区别：

例如上述情况：求区间和时7是加(r-l+1)* v，而求区间最值的时候子节点都加v，所以最大值也加v，就不存在求子节点个数的问题。

求区间和与求区间最值中pushdown函数也是一样的道理。

//求区间和的update中的判断
if (L <= l&&R >= r)
    {
        c[k] +=(r-l+1)* v;//注意这里
        lazy[k] += v;
    }

//求区间最值的update中的判断
    if (L <= l&&R >= r) //如果当前结点的区间真包含于要更新的区间内
    {
        lazy[k] += v; //懒惰标记
        c[k] += v; //最大值加上v之后，此区间的最大值也肯定是加v
    }

线段树的区间查询

int query(int L, int R, int l, int r, int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        pushdown(k,l,r); /*每次都需要更新子树的Lazy标记*///这里改变了
        int res = 0;
        int m = l + ((r - l) >> 1);
        if (L <= m)res += query(L, R, l, m, k << 1);
        if (m < R)res +=query(L, R, m + 1, r, k << 1 | 1);
        return res;
    }
}

代码汇总

#include<iostream>
#include<algorithm>
using namespace std;
#define MAX 100
#define INF 0x3f3f3f3f
int a[MAX], c[MAX << 2], lazy[MAX << 2];//空间，一般会开到4*n的空间防止RE。
void build(int k, int l, int r)
{
    if (l == r)//如果是最后的叶子节点，就直接赋值
        c[k] = a[l];
    else
    {
        int m = l + ((r - l) >> 1);//注意这里的括号，进行优先级的处理
        build(k << 1, l, m);//不是的话就递归
        build(k << 1 | 1, m + 1, r);
        c[k] = c[k << 1]+ c[k << 1 | 1];//由于不是最后的叶子节点，所以一定有左右子节点，所以此节点的值就是左右子节点较大的值
    }
}

void pushdown(int k,int l,int r)
{
    if (lazy[k])
    {
        int m = (l + r) >> 1;
        lazy[k << 1] += lazy[k];
        lazy[k << 1 | 1] += lazy[k];
        c[k << 1] += lazy[k]*(m-l+1);
        c[k << 1 | 1] += lazy[k]*(r-(m+1)+1);
        lazy[k] = 0;
    }
}
void update(int L, int R, int v, int l, int r, int k)
{
    if (L <= l&&R >= r)
    {
        c[k] +=(r-l+1)* v;
        lazy[k] += v;
    }
    else
    {
        pushdown(k,l,r);
        int m = l + ((r - l) >> 1);
        if (L <= m)
            update(L, R, v, l, m, k << 1);
        if (R >m)
            update(L, R, v, m + 1, r, k << 1 | 1);
        c[k] = c[k << 1]+ c[k << 1 | 1];
    }

}
int query(int L, int R, int l, int r, int k)
{
    if (L <= l&&R >= r)
        return c[k];
    else
    {
        pushdown(k,l,r); /**每次都需要更新子树的Lazy标记*/
        int res = 0;
        int m = l + ((r - l) >> 1);
        if (L <= m)res += query(L, R, l, m, k << 1);
        if (m < R)res +=query(L, R, m + 1, r, k << 1 | 1);
        return res;
    }
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    build(1, 1, n);
    printf("更改前的线段树数组c[]：");
    for (int i = 1; i <= (n << 1 | 1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的和：");
    printf("%d", query(2, 5, 1, n, 1));
    update(2, 5, 1, 1, n, 1);//2~5都加1
    printf("
");
    printf("更改后的线段树数组c[]：");
    for (int i = 1; i <= (n << 1 | 1); i++)
        printf("%s%d", i == 1 ? "" : " ", c[i]);
    printf("
");
    printf("输出【2，5】的和：");
    printf("%d", query(2, 5, 1, n, 1));
}

参考：https://www.cnblogs.com/xenny/p/9801703.html

相关阅读:
计算机体系结构的铁律（iron law）
PHP 画图——使用jpgraph画图
 理解Paxos Made Practical
【bzoj1015】【JSOI2008】【星球大战】【并查集+离线】
Spark调研笔记第3篇
 hduoj2094产生冠军
 使用HD/IDE层的ioctl接口获取磁盘容量get_hdd_max_sector
给GridView设置行高
 tomcat的一些简单配置
 【JavaScript】--JavaScript总结一览无余
原文地址：https://www.cnblogs.com/Jason66661010/p/12800443.html