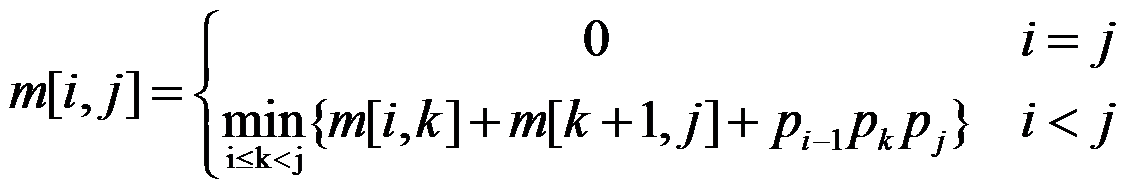矩阵连乘 动态规划

　　题目描述：给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1,2 ,…,n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。例如：

　　A1={30x35} ; A2={35x15} ;A3={15x5} ;A4={5x10} ;A5={10x20} ;A6={20x25} ;

最后的结果为：((A1(A2A3))((A4A5)A6))  最小的乘次为15125。

　　解题思路：能用动态规划的一个性质就是最优子结构性质，也就是说计算A[i:j]的最优次序所包含的计算矩阵子琏A[i:k]和A[k+1:j]的次序也是最优的。动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算（即先从最小的开始计算）。在计算过程中，保存已解决的子问题答案。每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量的重复计算，最终得到多项式时间的算法。我们可以根据下面这个公式来计算结果。其中p[i-1]表示的是第i个矩阵的行数,p[k]表示i:k矩阵合起来后最后得到的列数，p[j]是k+1:j合起来后得到的列数。这个部分的计算方法其实就是计算两个矩阵相乘时总共的乘次数，自己琢磨琢磨就明白了。

从连乘矩阵个数为2开始计算每次的最小乘次数m[i][j]: m[0][1] m[1][2] m[2][3] m[3][4] m[4][5]  //m[0][1]表示第一个矩阵与第二个矩阵的最小乘次数

然后再计算再依次计算连乘矩阵个数为3:m[0][2] m[1][3] m[2][4] m[3][5]

　　　　　　　　　   连乘矩阵个数为4：m[0][3] m[1][4] m[2][5]

　　　　　　　　　　连乘矩阵个数为5：m[0][4] m[1][5]

　　　　　　　　　　连乘矩阵个数为6：m[0][5]    //即最后我们要的结果

代码：

#include <stdio.h>
#include <stdlib.h>

#define MAX 100


int matrix_chain(int *p, int n, int **m, int **s)
{
    //a[][]最小乘次数
    //s[][]最小乘数时的断开点
    int i,j,r,k;
    
    for (i = 0; i < n; i++)   //单一矩阵的最小乘次都置为0
    {
        m[i][i] = 0;
    }
    
    for (r = 2; r <= n; r++)  //r为连乘矩阵的个数
    {
        for (i = 0; i <= n-r; i++)   //i表示连乘矩阵中的第一个
        {
            j = i + r -1;         //j表示连乘矩阵中的最后一个
            m[i][j] = 99999;
            for (k = i; k <= j-1; k++)  //在第一个与最后一个之间寻找最合适的断开点，注意，这是从i开始，即要先计算两个单独矩阵相乘的乘次
            {
                int tmp = m[i][k] + m[k+1][j] + p[i]*p[k+1]*p[j+1];
                if (tmp < m[i][j])
                {
                    m[i][j] = tmp;
                    s[i][j] = k;
                }
            }
        }
    }
    return m[0][n-1];
}

void print_chain(int i, int j, char **a,int **s)
{    //递归的方式来把最小乘数的表达式输出

    if (i == j)
    {
        printf("%s",a[i]);
    }
    else
    {
        printf("(");
        print_chain(i,s[i][j],a,s);
        print_chain(s[i][j]+1,j,a,s);
        printf(")");
    }
}

int main()
{
    //min_part[i][j]存储的是i+1到j+1的最小乘次，因为是从0开始
    //min_point[i][j]存储的是i+1到j+1之间最小乘次时的分割点
    int *p, **min_part, **min_point;
    char **a;
    int n = 6,i;
    int ret;
    
    p = (int *)malloc((n+1)*sizeof(int));
    a = (char **)malloc(n*sizeof(char*));
    min_part = (int **)malloc(n*sizeof(int *));
    min_point = (int **)malloc(n*sizeof(int *));
    
    for (i = 0; i < n; i++)
    {
        min_part[i] = (int *)malloc(n*sizeof(int));  
        min_point[i] = (int *)malloc(n*sizeof(int));
        a[i] = (char *)malloc(n*sizeof(char));
    }
    
    p[0] = 30;   //第一个矩阵的行数
    p[1] = 35;     //第二个矩阵的行数
    p[2] = 15;     //……
    p[3] = 5;     //……    
    p[4] = 10;     //……
    p[5] = 20;     //第六个矩阵的行数
    p[6] = 25;     //第六个矩阵的列数
    
    a[0] = "A1";
    a[1] = "A2";
    a[2] = "A3";
    a[3] = "A4";
    a[4] = "A5";
    a[5] = "A6";
    
    ret = matrix_chain(p,n,min_part,min_point);
    printf("Minest times:%d.
",ret);
    print_chain(0,n-1,a,min_point);
    
    free(p);
    free(min_part);
    free(min_point);
    free(a);

    return 0;
}

2013/8/1 23:38