[ICPC USA]Faulty Robot (搜索)

原题目

As part of a CS course,Alice just finished programming her robot to explore a graph having nn nodes,labeled 1,2,...,n,1,2,...,n, and mm directed edges. Initially the robot starts at node (1).

While nodes may have several outgoing edges, Alice programmed the robot so that any node may have a forced move to a specific one of its neighbors. For example, it may be that node 55 has outgoing edges to neighbors 1, 41,4, and 66 but that Alice programs the robot so that if it leaves 55 it must go to neighbor 44.

If operating correctly, the robot will always follow forced moves away from a node, and if reaching a node that does not have a forced move,the robot stops. Unfortunately,the robot is a bit buggy,and it might violate those rules and move to a randomly chosen neighbor of a node (whether or not there had been a designated forced move from that node). However, such a bug will occur at most once (and might never happen).

Alice is having trouble debugging the robot, and would like your help to determine what are the possible nodes where the robot could stop and not move again.

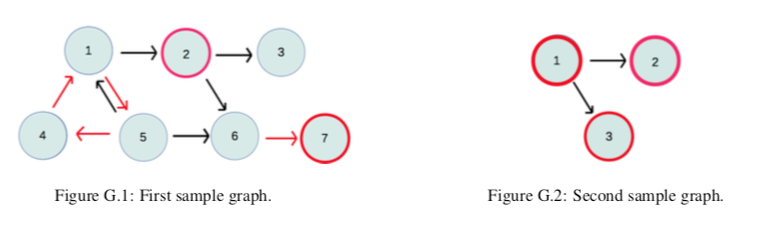
We consider two sample graphs, as given in Figures G.1 and G.2. In these figures, a red arrow indicate an edge corresponding to a forced move, while black arrows indicate edges to other neighbors. The circle around a node is red if it is a possible stopping node.

题意

一个有向图从①出发，最多有一次不走红边而走其他出边的机会（bug），问能停在几个点上

思路

一道很简单调了一个晚上Orz的搜索题
结构体存储边的信息，将红边放在每个点的头部，能优化一下常数
从①开始进行DFS，可以根据之前有没有出过bug，选择按红边走或者不按红边走，如果选择不按红边走就在搜索参数上面调整为出过bug，直到到一个不能再操作的点为止，答案+1

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>

using namespace std;
const int maxn=1e3+10;
struct node
{
	int to,tp;
	node(int to,int tp):to(to),tp(tp){}
};
vector<node> g[maxn];
bool vis[maxn],fst[maxn];                                            //vis是是否进行过搜索的点，fst是标记最后停下来的点
int n,m,cnt;

void dfs(int cur,bool bug)
{
	int sz=g[cur].size();
	if(sz==0)
	{
		if(!fst[cur])	
			fst[cur]=1,cnt++;
		return ;
	}
	else if(g[cur][0].tp==1)
	{
		if(!fst[cur])
			fst[cur]=1,cnt++;
	}
	if(bug)
	{
		if(g[cur][0].tp==2&&!vis[g[cur][0].to])
			vis[g[cur][0].to]=1,dfs(g[cur][0].to,bug);
		return ;
	}
	else
	{
		
		for(int i=0;i<sz;++i)
		{
			if(!vis[g[cur][i].to])
			{
				vis[g[cur][i].to]=1;
				if(g[cur][i].tp==2)
				{
					dfs(g[cur][i].to,0);         //使用fst标记答案点是为了防止`出现或者不出现bug都按红边而出现的重复计数`
					dfs(g[cur][i].to,1);
				}
				else
				{
					dfs(g[cur][i].to,1);
				}
			}
		}
	}
}


int main()
{
	cin>>n>>m;
	if(m==0)
	{
		cout<<0;
		return 0;
	}
	int s,e;
	for(int i=1;i<=m;++i)
	{
		scanf("%d%d",&s,&e);
		if(s>0)	g[s].push_back(node(e,1));
		else g[-s].insert(g[-s].begin(),node(e,2));
	}
	dfs(1,0);
	cout<<cnt;
	return 0;
}

看到了跟dalao之间的差距，得更加努力了，猛练自然强，加油！！