支持向量机 (support vector machine, SVM) 是建立在统计学习理论的 VC 维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特点训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折中,以期获得最好的泛化能力。
支持向量机的基本思想,简单地说,是通过某种事先选择的非线性映射,将输入向量映射到一个高维特征空间中,在这个空间里构造最优分类超平面,将不同类别的样本分开。所谓超平面,就是一个比原特征空间少一个维度的子空间,在二维情况下就是一条直线,在三维情况下就是一个平面。
支持向量机的核心:它希望找到这一一条线,使得正负样本之间的间隙越大越好,这是因为距离分类超平面越近的样本,分类的置信度越低(即最难分类的样本),如果能将这些最难分类的点也能尽可能分离开,那么预测的效果会更好。SVM算法的目标就是最大化最接近分类超平面的样本距离超平面的距离,即最大化分类间隔。
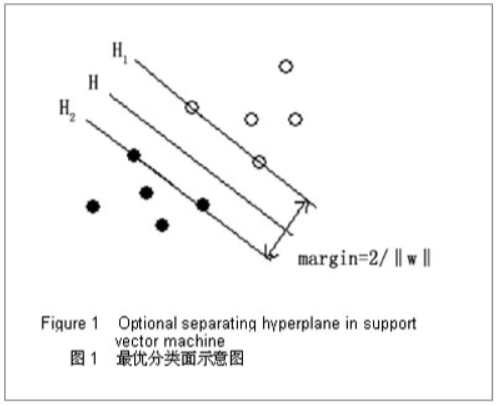
如上图所示,H 表示分类线,(H_1)、(H_2) 分别是经过各类样本中距离分类线最近的样本并且平行于分类线的直线,它们之间的间隔叫作分类间隔 (margin)。其中,(H_1)、(H_2) 这两条直线对应的向量即支持向量。
线性支持向量机
硬间隔
由于训练数据完全可以由分离超平面分开,我们不需要容忍任何训练数据中出现的异常点,因此这样的间隔称为硬间隔(如上面的图1所示)。
求解最优超平面其实是一个二次规划问题,实际算法中,已经有许多成熟的算法以及工具来求解,我们一般把它作为一个黑箱来看待。
软间隔
硬间隔是训练数据线性可分的状况。然而现实中的训练数据并不都那么理想,更多情况下是找不到这样的分离超平面把训练数据中的正例和负例完全分开的;有时候可以找到一个分离超平面“勉强”地分开正例和负例,但是为了使得正例和负例完全分开,间隔变得非常小,因此这样的分离超平面泛化能力很差。
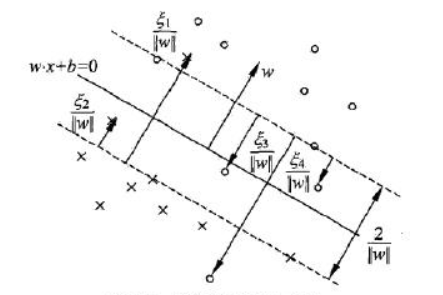
为了解决这样的问题,对于近似于线性可分的训练样例,我们可以在某种程度上“容忍”样本点落在 (H_1) 与 (H_2) 之间(如下图所示),但是又要采取措施“惩罚”这些偏离,使得“容忍”的程度尽可能地低。
非线性支持向量机
有些时候,训练数据连近似的线性划分也找不到,线性超平面无法有效划分正类与负类,而是需要超曲面等非线性的划分。因此通常的做法是引入核函数,将低维度不可分的数据映射到高维后,变成了线性可分的数据,这时候再使用线性支持向量机。
常用的核函数有:
线性核函数
其实就是线性支持向量机。
多项式核函数
高斯核函数
Sigmoid核函数
其实实现的就是一种多层神经网络。
算法的优缺点
优点:
(1)可以解决小样本下的机器学习问题。
(2)模型鲁棒性能强,SVM 最终的分类效果只由少数支持向量决定,增删数据集中的非支持向量样本对分类结果不会有影响。
(3)可以处理线性和非线性数据。
缺点:
(1)对大规模训练样本需消耗大量内存。
(2)模型的可解释性较弱。
(3)对多分类问题的处理比较困难。
Demo
使用 SVM 对 Digits 数据集进行分类。
Jupyter Notebook 链接为:SVM-Digits
【References】
[1] 裔隽,张怿檬,张目清等.Python机器学习实战[M].北京:科学技术文献出版社,2018