在宽度优先和深度优先搜索里面，我们都是根据搜索的顺序依次进行搜索，可以称为盲目搜索，搜索效率非常低。
而启发式搜索则大大提高了搜索效率，由这两张图可以看出它们的差别：
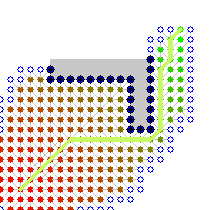（左图类似与盲搜，右图为启发式搜索）(图片来源) 
很明显启发式的搜索效率远远大于盲搜。
什么是启发式搜索（heuristic search）
利用当前与问题有关的信息作为启发式信息，这些信息是能够提升查找效率以及减少查找次数的。
如何使用这些信息，我们定义了一个估价函数 h(x) 。h(x)是对当前状态x的一个估计，表示 x状态到目标状态的距离。
有：1、h(x) >= 0 ； 2、h(x)越小表示 x 越接近目标状态； 3、如果 h(x) ==0 ，说明达到目标状态。
与问题相关的启发式信息都被计算为一定的 h(x) 的值，引入到搜索过程中。
然而，有了启发式信息还不行，还需要起始状态到 x 状态所花的代价，我们称为 g(x) 。比如在走迷宫问题、八数码问题，我们的 g(x) 就是从起点到 x 位置花的步数 ，h(x) 就是与目标状态的曼哈顿距离或者相差的数目；在最短路径中，我们的 g(x) 就是到 x 点的权值，h(x) 就是 x 点到目标结点的最短路或直线距离。
现在，从 h(x) 和 g(x) 的定义中不能看出，假如我们搜索依据为 F(x) 函数。
当 F(x) = g(x) 的时候就是一个等代价搜索，完全是按照花了多少代价去搜索。比如 bfs，我们每次都是从离得近的层开始搜索，一层一层搜 ；以及dijkstra算法，也是依据每条边的代价开始选择搜索方向。
当F(x) = h(x) 的时候就相当于一个贪婪优先搜索。每次都是向最靠近目标的状态靠近。
人们发现，等代价搜索虽然具有完备性，能找到最优解，但是效率太低。贪婪优先搜索不具有完备性，不一定能找到解，最坏的情况下类似于dfs。
这时候，有人提出了A算法。令F(x) = g(x) + h(x) 。（这里的 h(x) 没有限制）。虽然提高了算法效率，但是不能保证找到最优解，不适合的 h(x)定义会导致算法找不到解。不具有完备性和最优性。
几年后有人提出了 A*算法。该算法仅仅对A算法进行了小小的修改。并证明了当估价函数满足一定条件，算法一定能找到最优解。估价函数满足一定条件的算法称为A*算法。
它的限制条件是 F(x) = g(x) + h(x) 。 代价函数g(x) >0 ；h(x) 的值不大于x到目标的实际代价 h*(x) 。即定义的 h(x) 是可纳的，是乐观的。
怎么理解第二个条件呢？
打个比方：你要从x走到目的地，那么 h(x) 就是你感觉或者目测大概要走的距离，h*(x) 则是你到达目的地后，发现你实际走了的距离。你预想的距离一定是比实际距离短，或者刚好等于实际距离的值。这样我们称你的 h(x) 是可纳的，是乐观的。
不同的估价函数对算法的效率可能产生极大的影响。尤其是 h(x) 的选定，比如在接下来的八数码问题中，我们选择了曼哈顿距离之和作为 h(x) ，你也可以选择相差的格子作为 h(x)，只不过搜索的次数会不同。当 h(x) 越接近 h*(x) ，那么扩展的结点越少！
那么A*算法的具体实现是怎么样的呢？
1、将源点加入open表
2、
while(OPEN!=NULL)
{
从OPEN表中取f(n)最小的节点n;
if(n节点==目标节点)
break;
for(当前节点n的每个子节点X)
{
计算f(X);
if(XinOPEN)
if(新的f(X)<OPEN中的f(X))
{
把n设置为X的父亲;
更新OPEN表中的f(n); //不要求记录路径的话可以直接加入open表，旧的X结点是不可能比新的先出队
}
if(XinCLOSE)
continue;
if(Xnotinboth)
{
把n设置为X的父亲;
求f(X);
并将X插入OPEN表中;
}
}//endfor
将n节点插入CLOSE表中;
按照f(n)将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。
}//endwhile(OPEN!=NULL)
3、保存路径，从目标点出发，按照父节点指针遍历，直到找到起点。
以八数码问题为例：
我们从1、仅考虑代价函数； 2、仅考虑贪婪优先； 3、A*算法。
1 #include<bits/stdc++.h> 2 using namespace std; 3 struct Maze{ 4 char s[3][3]; 5 int i,j,fx,gx; 6 bool operator < (const Maze &a )const{ 7 return fx>a.fx; 8 } 9 } c; 10 int fx[4][2]={{-1,0},{1,0},{0,1},{0,-1}}; 11 map<char ,Maze > mp; 12 int T; 13 int get_hx(char s[3][3]){ 14 int hx=0; 15 for(int i=0;i<3;i++){ 16 for(int j=0;j<3;j++){ 17 hx+=abs(mp[s[i][j]].i-i)+abs(mp[s[i][j]].j-j); 18 } 19 } 20 return (int)hx; 21 } 22 void pr(char s[3][3]){ 23 cout<<"step: "<<T++<<endl; 24 for(int i=0;i<3;i++){ 25 for(int j=0;j<3;j++) 26 cout<<s[i][j]; 27 cout<<endl; 28 } 29 cout<<endl; 30 } 31 int key(char s[3][3]){ 32 int ans=0; 33 for(int i=0;i<3;i++) 34 for(int j=0;j<3;j++) 35 ans=ans*10+(s[i][j]-'0'); 36 return ans; 37 } 38 void BFS(){ 39 T=0; 40 map<int ,bool >flag; 41 queue < Maze > q; 42 q.push(c); 43 flag[key(c.s)]=1; 44 while(!q.empty()){ 45 Maze now=q.front(); 46 q.pop(); 47 pr(now.s); 48 if(get_hx(now.s)==0){ 49 break; 50 } 51 for(int i=0;i<4;i++){ 52 int x,y; 53 x=now.i+fx[i][0]; 54 y=now.j+fx[i][1]; 55 if(!(x>=0&&x<3&&y>=0&&y<3)) continue; 56 Maze tmp=now; 57 tmp.s[now.i][now.j]=tmp.s[x][y]; 58 tmp.s[x][y]='0'; 59 tmp.i=x ; tmp.j=y ; 60 tmp.fx++; 61 if(!flag[key(tmp.s)]){ 62 q.push(tmp); 63 flag[key(tmp.s)]=1; 64 } 65 } 66 } 67 } 68 void Greedy_best_first_search(){ 69 T=0; 70 priority_queue< Maze > q ; 71 map<int ,int >flag; 72 c.fx=get_hx(c.s); 73 q.push(c); 74 flag[key(c.s)]=1; 75 while(!q.empty()){ 76 Maze now=q.top(); 77 q.pop(); 78 pr(now.s); 79 if(get_hx(now.s)==0){ 80 break; 81 } 82 for(int i=0;i<4;i++){ 83 int x,y; 84 x=now.i+fx[i][0]; 85 y=now.j+fx[i][1]; 86 if(!(x>=0&&x<3&&y>=0&&y<3)) continue; 87 Maze tmp=now; 88 tmp.s[now.i][now.j]=tmp.s[x][y]; 89 tmp.s[x][y]='0'; 90 tmp.i=x ; tmp.j=y ; 91 tmp.fx=get_hx(tmp.s); 92 if(!flag[key(tmp.s)]){ 93 q.push(tmp); 94 flag[key(tmp.s)]=1; 95 } 96 } 97 } 98 } 99 void A_star(){ 100 T=0; 101 priority_queue< Maze > q ; 102 map<int ,int >flag; 103 c.gx=0; 104 c.fx=get_hx(c.s)+c.gx; 105 q.push(c); 106 while(!q.empty()){ 107 Maze now=q.top(); 108 q.pop(); 109 flag[key(now.s)]=now.fx; 110 pr(now.s); 111 if(get_hx(now.s)==0){ 112 break; 113 } 114 for(int i=0;i<4;i++){ 115 int x,y; 116 x=now.i+fx[i][0]; 117 y=now.j+fx[i][1]; 118 if(!(x>=0&&x<3&&y>=0&&y<3)) continue; 119 Maze tmp=now; 120 tmp.s[now.i][now.j]=tmp.s[x][y]; 121 tmp.s[x][y]='0'; 122 tmp.i=x ; tmp.j=y ; 123 tmp.gx++; 124 tmp.fx=get_hx(tmp.s)+tmp.gx; 125 if(!flag[key(tmp.s)]){ 126 q.push(tmp); 127 }else if(flag[key(tmp.s)]>tmp.fx){ 128 flag[key(tmp.s)]=0; 129 q.push(tmp); 130 } 131 } 132 } 133 } 134 int main(){ 135 mp['1'].i=0;mp['1'].j=0; 136 mp['2'].i=0;mp['2'].j=1; 137 mp['3'].i=0;mp['3'].j=2; 138 mp['4'].i=1;mp['4'].j=2; 139 mp['5'].i=2;mp['5'].j=2; 140 mp['6'].i=2;mp['6'].j=1; 141 mp['7'].i=2;mp['7'].j=0; 142 mp['8'].i=1;mp['8'].j=0; 143 mp['0'].i=1;mp['0'].j=1; 144 for(int i=0;i<3;i++){ 145 for(int j=0;j<3;j++){ 146 cin>>c.s[i][j]; 147 } 148 char x=getchar(); 149 } 150 cin>>c.i>>c.j; 151 c.fx=0; 152 cout<<"八数码问题 BFS 解法(即仅以当前代价 g(x)搜索): "<<endl; 153 BFS(); 154 cout<<"八数码问题 Greedy_best_first_search 解法(即仅以估计函数 h(x)搜索): "<<endl; 155 Greedy_best_first_search(); 156 cout<<"八数码问题 A* 解法: "<<endl; 157 A_star(); 158 return 0; 159 } 160 /* 161 283 162 164 163 705 164 2 1 165 */
结果显示：
1、仅考虑代价函数：36步。
2、仅考虑贪婪优先：5步。
3、A*算法：5步。
明显，在引入了启发式信息后，大大的提高了搜索的效率。
引申问题： 第 k 短路问题。
思路： 先从终点求出最短路，作为 h(x) 。然后维护优先队列，维护 F(x) 最小，第一次出来的终点是最短路，终点第二次出来的是次短路……
求第k短路时，A*算法优化的是查找的次数，可以理解为剪枝，更快速的找到最短路，次短路……
其他操作和正常的求最短路没有什么区别，找到终点第k次出队的值，就是第k短路。
（可能你会说在无向图中存在有回头路，没错，有可能次短路只是最短路走了一次回头路，但这确实也是一条次短路）。