离散无记忆信道容量的迭代算法（Bluhat Arimoto算法）

import numpy as np


def blahut_arimoto(p_y_x: np.ndarray,  log_base: float = 2, thresh: float = 1e-12, max_iter: int = 1e3) -> tuple:
    '''
    Maximize the capacity between I(X;Y)
    p_y_x: each row represnets probability assinmnet
    log_base: the base of the log when calaculating the capacity
    thresh: the threshold of the update, finish the calculation when gettting to it.
    max_iter: the maximum iterations of the calculation
    '''

    # Input test
    assert np.abs(p_y_x.sum(axis=1).mean() - 1) < 1e-6
    assert p_y_x.shape[0] > 1

    # The number of inputs: size of |X|
    m = p_y_x.shape[0]

    # The number of outputs: size of |Y|
    n = p_y_x.shape[1]

    # Initialize the prior uniformly
    r = np.ones((1, m)) / m

    # Compute the r(x) that maximizes the capacity
    for iteration in range(int(max_iter)):

        q = r.T * p_y_x
        q = q / np.sum(q, axis=0)

        r1 = np.prod(np.power(q, p_y_x), axis=1)
        r1 = r1 / np.sum(r1)

        tolerance = np.linalg.norm(r1 - r)
        r = r1
        if tolerance < thresh:
            break

    # Calculate the capacity
    r = r.flatten()
    c = 0
    for i in range(m):
        if r[i] > 0:
            c += np.sum(r[i] * p_y_x[i, :] *
                        np.log(q[i, :] / r[i] + 1e-16))
    c = c / np.log(log_base)
    return c, r

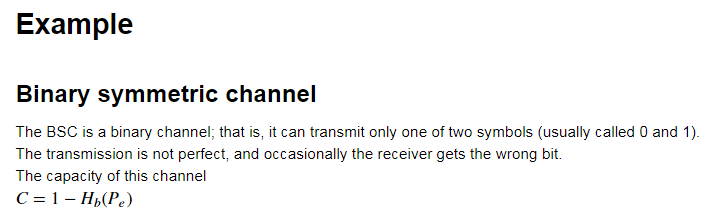
e = 0.2
p1 = [1-e, e]
p2 = [e, 1-e]
p_y_x = np.asarray([p1, p2])
C, r = blahut_arimoto(p_y_x)
print('Capacity: ', C)
print('The prior: ', r)

# The analytic solution of the capaciy
H_P_e = - e * np.log2(e) - (1-e) * np.log2(1-e)
print('Anatliyic capacity: ', (1 - H_P_e))

输出为：

Capacity:  0.2780719051126379
The prior:  [0.5 0.5]
Anatliyic capacity:  0.2780719051126377

e = 0.1
p1 = [1-e, e, 0]
p2 = [0, e, 1-e]
p_y_x = np.asarray([p1, p2])
C, r = blahut_arimoto(p_y_x, log_base=2)
print('Capacity: ', C)
print('The prior: ', r)

# The analytic solution of the capaciy
print('Anatliyic capacity: ', (1 - e))

输出为：

Capacity:  0.9
The prior:  [0.5 0.5]
Anatliyic capacity:  0.9

! jupyter nbconvert blahut_arimoto_algorithm.ipynb --to="python" --output-dir .   #将jupyter notebook下的.ipynb文件另存为.py文件

完整实战代码为：

# 2019年11月9日17:01:21
import numpy as np

def bluhat_arimoto(p_y_x: np.ndarray, thresh: float = 1e-12, max_iter: int = 1e3) -> tuple:
    '''
    Maximize the capacity between I(X;Y)
    p_y_x: each row represnets probability assinmnet
    thresh: the threshold of the update, finish the calculation when gettting to it.
    max_iter: the maximum iterations of the calculation
    '''

    # 检查输入是否符合要求
    assert np.abs(p_y_x.sum(axis=1).mean() - 1) < 1e-6,'转移概率矩阵不符合要求'  #axis=1表示矩阵每一行相加    .mean()表示矩阵所有元素的平均值
    assert p_y_x.shape[0] > 1,'至少要有两个信源'

    # 信源信宿的个数
    m = p_y_x.shape[0]  #有 m 个信源
    n = p_y_x.shape[1]  #有 n 个信宿

    # 初始化输入分布r(x)为等概分布
    r = np.ones((1, m)) / m

    # Compute the r(x) that maximizes the capacity
    for iteration in range(int(max_iter)):

        Q = r.T * p_y_x
        Q = Q / np.sum(Q, axis=0)  # Q的每一列相加

        r1 = np.prod(np.power(Q, p_y_x), axis=1) #power(x, y)，计算 x 的 y 次方; np.prod()计算数组元素乘积
        r1 = r1 / np.sum(r1)

        tolerance = np.linalg.norm(r1 - r)  #范数是一个标量，默认计算L2范数
        r = r1
        if tolerance < thresh:
            break

    # Calculate the capacity
    r = r.flatten()  #将矩阵转化为一维数组
    C = 0
    for i in range(m):
        if r[i] > 0:
            C += np.sum(r[i] * p_y_x[i, :] * np.log2(Q[i, :] / r[i])) # 公式4.3.14
    return C, r


# e = 0.1
# p1 = [1-e, e, 0]
# p2 = [0, e, 1-e]

p1 = [0.5, 0.3, 0.2]
p2 = [0.3, 0.5, 0.2]

# p1 = [1/3, 1/3, 1/6, 1/6]
# p2 = [1/6, 1/3, 1/6, 1/3]

# p1 = [1/3, 1/3, 0, 1/3]
# p2 = [0, 1/3, 1/3, 1/3]
# p3 = [1/3, 0, 1/3, 1/3]

# p1 = [1, 0, 0]
# p2 = [0, 1/2, 1/2]
# p3 = [0, 1/2, 1/2]

# p1 = [1, 0, 0]
# p2 = [0, 1, 0]
# p3 = [0, 0, 1]
#
# p1 = [1/2, 1/2, 0, 0]
# p2 = [0, 1/2, 1/2, 0]
# p3 = [0, 0, 1/2, 1/2]
# p4 = [1/2, 0, 0, 1/2]

p_y_x = np.asarray([p1, p2])
print('信道转移概率矩阵P为：
')
print('P = {}
'.format(p_y_x))
C, r = bluhat_arimoto(p_y_x)
print('信道容量为: {:.4f}bit/符号'.format(C))
print('输入分布r(x)为: ', r)