分析这道题,爽,能够结合IDA和ollydbg分析代码,美滋滋。但如果以后能直接根据汇编容易地看懂逻辑那就更好了。
参考链接:
首先根据IDA分析得知主函数是sub_411B70()。查看功能,可知它先随机生成了二维随机数组序列(这其实是伪随机的),然后提示用户输入数,还有个可疑函数sub_41114F(),猜测会处理输入数,最后判断输入的数能在二维随机数组序列中顺利走多久。看回显可知要输入能走得最久且最终数字和最大的数(如下图),即既能走到数组头,又经过的所有点的随机数和最大。emmmm,牵扯到的点有PRNG和Maze(迷宫),哦,还有个加密。
(1)PRNG
它是一种伪随机数生成器(如下图),使用种子作为输入,攻击者知道种子和算法就能重现输出流。
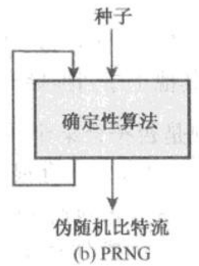

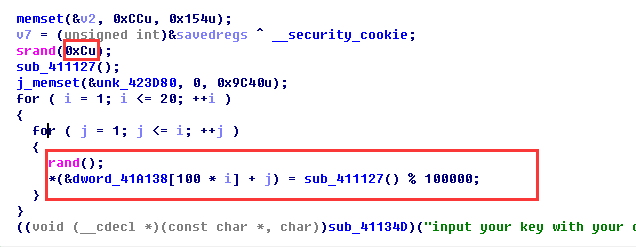
看上图,程序提供的种子一直是0xCu,则rand的值就是固定的,那就能复现这个随机数组啦。
(2)可疑函数sub_41114F()
使用ollydbg动态调试输入的数据,看经过这个函数后的输出数据,可知它将偶数位的字符都变化了,可以认为是单表替换加密,即将固定的字母换成了其他字母。
经过测试,得知它的替换结果如下。
原数 ABCDEFGHIJKLMNOPQRSTUVWXYZ
替换结果 EFG@ABCLMNOHIJKTUVWPQRS]^
(3)Maze(迷宫)
在迷宫中要想走出去且获取的值最大,起点已定,就要从当下着眼,每一步走最大的,这样结果才是最大的。迷宫算法如下图。
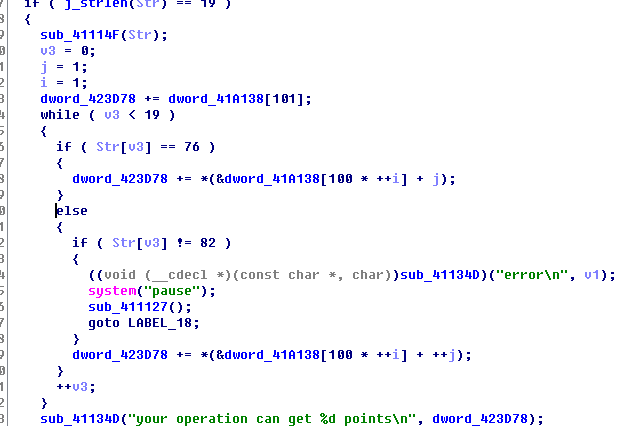
接下来开始破解。可以先复现逻辑数组,然后逆向思维算出最好的走法,最后将走法偶数位通过单表计算替换字符即可。程序如下:
#include<iostream>
using namespace std;
int main() {
int mountain[20][20];
memset(mountain, 0, 400 * sizeof(int));
srand(12);
for (int i = 1; i <= 20; ++i)
{
for (int j = 1; j <= i; ++j)
{
mountain[i][j] = rand() % 100000;
}
}
int x = 1, y = 1;
int sum = mountain[x][y];
for (int i = 0; i < 19; i++) {
int L = mountain[x + 1][y];
int R = mountain[x + 1][y + 1];
if (R > L) {
printf("R");
sum += R;
x++;
y++;
}
else {
printf("L");
sum += L;
x++;
}
}
printf("
%d
", sum);
system("pause");
return 0;
}
计算出来路线是RRRRRLLRRRLRLRRRLRL,通过单表计算结果是RVRVRHLVRVLVLVRVLVL,结果出来啦-。-