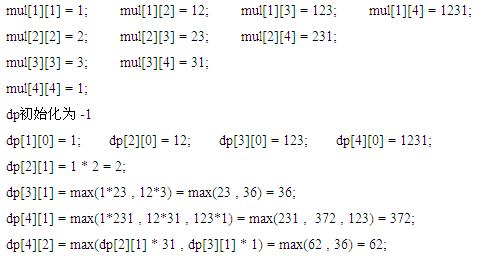DP是一个不能更常用的算法了,这里也就对基础的五大类DP题型做个总结。
目录
背包型
背包问题是很多教材上DP的引入题,它也确实是基础中的基础,总的来说背包型DP有01背包、部分背包、完全背包三种,其余的例如多重背包等都是衍生题目。直接看例题吧。
先看一道01背包。
Codevs 1014装箱问题
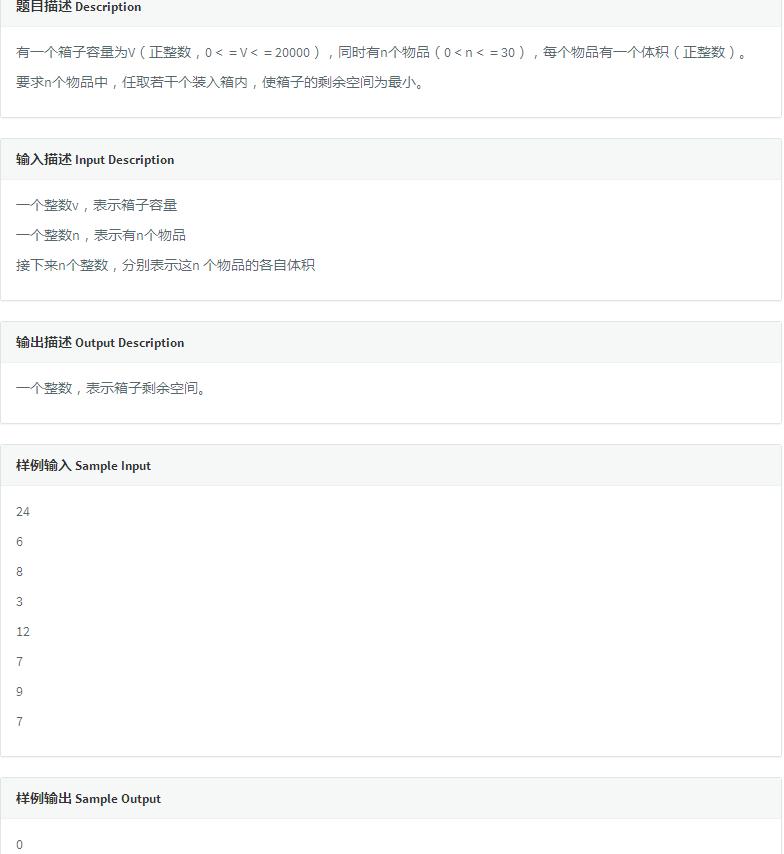
这类题目只有两种状态,拿或不拿,所以叫01背包。状态转移方程还是比较好写的:f[i] = max{f[i], f[i-x]+x}。f[i]表示选到i的最大容积(箱内容积),最后用总的去减去f[v]就是ans。
#include<iostream> using namespace std; int v, n, a; int f[100005]; int main() { cin >> v >> n; for (int i = 1; i <= n; i++) { cin >> a; for (int j = v ; j >= a; j--) { if (f[j] < f[j-a] + a) f[j] = f[j-a] + a; } } cout << v - f[v]; }
01背包就是这么简单。接下来看一道唬人一点的01背包。
Codevs 1068乌龟棋

这如果没有"数据保证到达终点时一定用完M张爬行卡片"这句话的话这道题会麻烦不少,但是有这句话的话就可以把它看做一个多维的01背包,用dp[a][b][c][d];来分别表示选四种卡的情况就可以了。
#include <cstdio> #include <iostream> using namespace std; int n, m; int map[500]; int dp[45][45][45][45]; template<class T>inline void read(T &res) { static char ch; while( (ch=getchar()) < '0' || ch > '9'); res = ch - 48; while( (ch = getchar() ) >= '0' && ch <= '9') res = ch - 48 + res * 10; } int main() { int a = 0; int b = 0; int c = 0; int d = 0; read(n); read(m); for (int i = 0; i < n; i++) read(map[i]); for (int k, i = 1; i <= m; i++) { read(k); if (k == 1) a++; if (k == 2) b++; if (k == 3) c++; if (k == 4) d++; } for (int i = 0; i <= a; i++) for (int j = 0; j <= b; j++) for (int k = 0; k <= c; k++) for (int e = 0; e <= d; e++) { if (i != 0) dp[i][j][k][e] = max(dp[i][j][k][e], dp[i - 1][j][k][e]); if (j != 0) dp[i][j][k][e] = max(dp[i][j][k][e], dp[i][j - 1][k][e]); if (k != 0) dp[i][j][k][e] = max(dp[i][j][k][e], dp[i][j][k - 1][e]); if (e != 0) dp[i][j][k][e] = max(dp[i][j][k][e], dp[i][j][k][e - 1]); dp[i][j][k][e] += map[i+(j*2)+(k*3)+(e*4)];//这一步很重要 } cout << dp[a][b][c][d]; return 0; }
看的出来其实也就是选或者不选的状态,只是维度比较多而已,还是比较裸的。
序列型
第二种题型是序列型。这类题目会让你维护一组数据的某个特性不变,比如保持单调性或是保持最优等等,这里也选了几道题来具体解释。
Codevs 1576最长严格上升子序列

最长不下降子序列就是在母序列中的一串下标递增,值也递增的序列,注意只需要满足下标递增就可以了,下标可以不连续。
这道题的转移方程也很简单:dp[i]表示当前长度,dp[i] = max{dp[i], dp[j]+1};不断更新长度就好,再用res去记录答案就可以了
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; int n, res; int a[1010]; int dp[1010]; int main() { cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; dp[n] = 1; for(int i = n; i >= 1; i--) for (int j = i+1; j <= n; j++) if (a[i] < a[j]) { dp[i] = max(dp[i], dp[j] + 1); res = max(res, dp[i]); } cout << res; return 0; }
下一道题是一道隐藏的深一点的序列DP。
Codevs 3027线段覆盖2
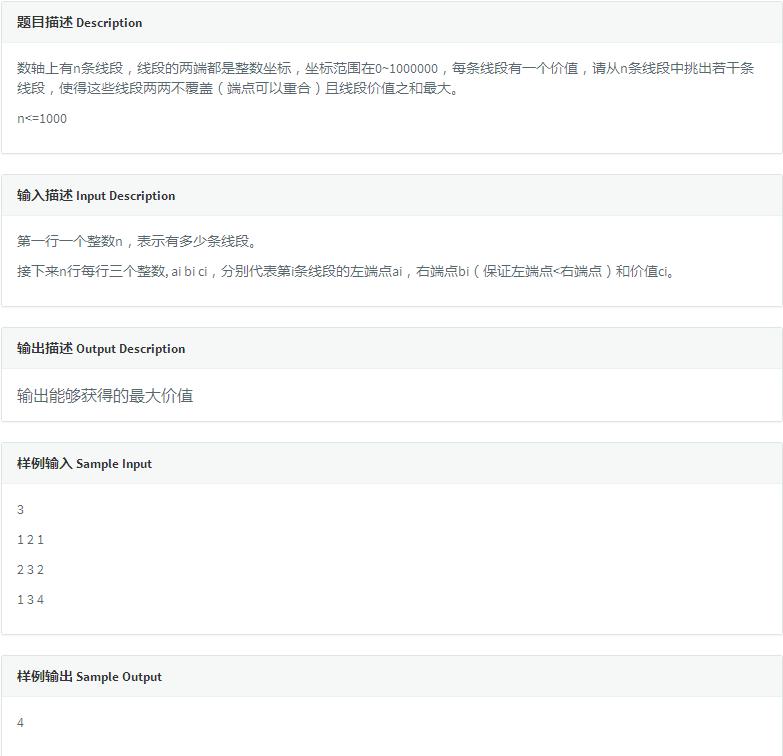
这道题还是比较有意思的,乍一看还以为是区间DP,实际上就是一个序列DP,只不过需要把数据预处理一下,按照右区间坐标排个序再来DP,就是一道裸的不能再裸的序列DP了。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define get(x) scanf("%d", &x) #define put(x) printf("%d", x) #define cln(x) memset(x, 0, sizeof(x)) using namespace std; int n, res; int dp[1010]; struct L { int l, r, c; }a[1010]; bool cmp(L a, L b) { return a.r < b.r; } int main() { get(n); for (int i = 1; i <= n; i++) { get(a[i].l), get(a[i].r), get(a[i].c); } sort(a+1, a+n+1, cmp); for (int i = 1; i <= n; i++) { int maxx = 0; for (int j = 1; j <= i; j++) if (a[i].l >= a[j].r) maxx = max(maxx, dp[j]); dp[i] = maxx + a[i].c; res = max(res, dp[i]); } put(res); return 0; }
棋盘型
这类DP题型大多可以用搜索来做,但是大部分的题目DP都要优于搜索,下面还是上例题吧。
Codevs 1219骑士游历
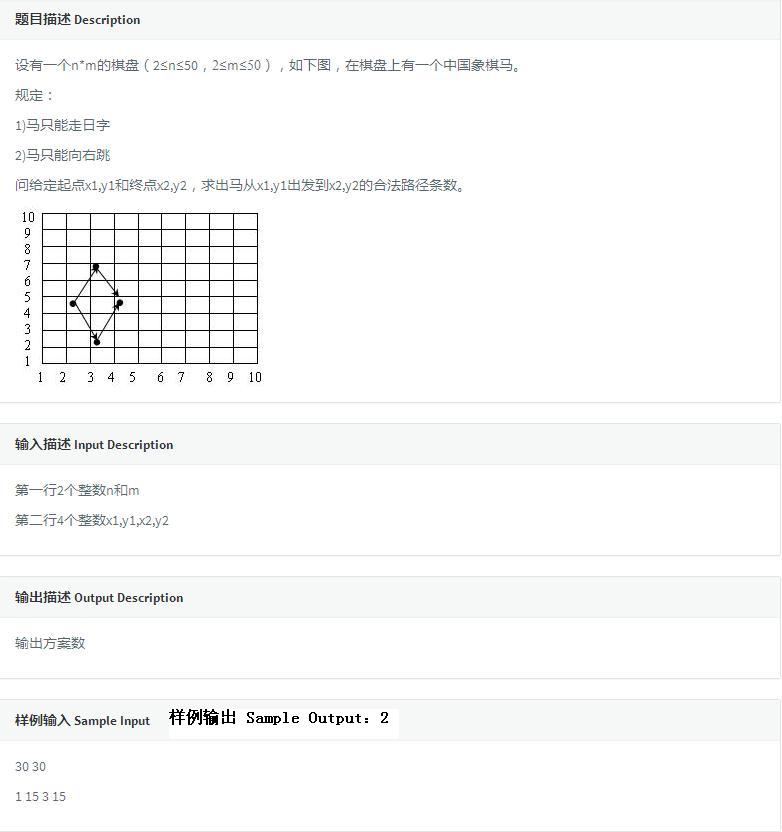
棋盘DP主要就是求合法路径数,而对于这道题,马只能走连个方向,而且不能回头。那么可以知道当前位置只可能经由p1或者p2到达,那么可以轻易写出转移方程dp[i][j] = dp[i-1][j+2] + dp[i-1][j-2] + dp[i-2][j+1] + dp[i-2][j-1],dp[i][j]表示从起始点p(x1, y1)到当前p(i, j)的合法路径数,初始化dp[x1][y1] = 1。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define lnt long long #define get(x) scanf("%lld", &x) #define put(x) printf("%lld", x) #define cln(x) memset(x, 0, sizeof(x)) using namespace std; lnt dp[60][60]; lnt n, m; lnt x1, y1, x2, y2; int main() { get(n), get(m); get(x1), get(y1), get(x2), get(y2); dp[x1][y1] = 1; for (int i = x1+1; i <= n; i++) for (int j = 1; j <= m; j++) { dp[i][j] = dp[i-1][j+2] + dp[i-1][j-2] + dp[i-2][j-1] + dp[i-2][j+1]; } put(dp[x2][y2]); return 0; }
看下一道题吧。
Codevs 1010过河卒
题目描述
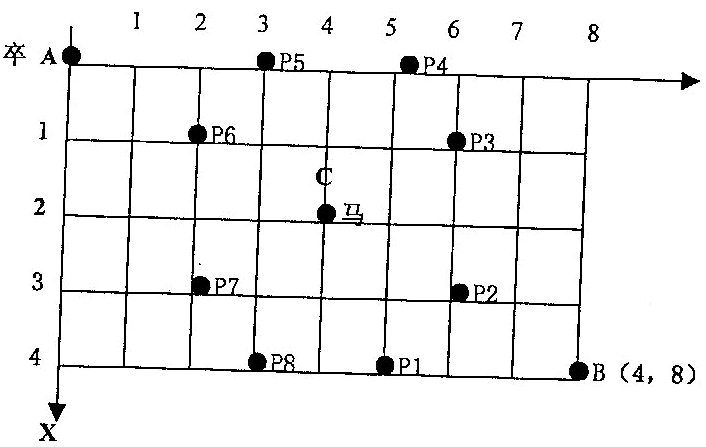
如图,A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如上图的C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点(图中的P1,P2 … P8 和 C)。卒不能通过对方马的控制点。
棋盘用坐标表示,A 点(0,0)、B 点(n,m)(n,m 为不超过 20 的整数,并由键盘输入),同样马的位置坐标是需要给出的(约定: C不等于A,同时C不等于B)。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。
1<=n,m<=15
输入描述
键盘输入
B点的坐标(n,m)以及对方马的坐标(X,Y){不用判错}输出描述
屏幕输出
一个整数(路径的条数)。输入描述(Sample Input)
6 6 3 2
输出描述(Sample Output)
17
这道题大体和骑士游历很像,转移方程也很好写dp[i][j] = max{dp[i-1][j], dp[i][j-1]},但是这道题有个马的机制,所以数据需要预处理,总的来说还是一道比较标准的棋盘DP。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define get(x) scanf("%d", &x) #define put(x) printf("%d", x) #define cln(x) memset(x, 0, sizeof(x)) using namespace std; int n, m; int x2, y2; int dp[50][50]; int main() { get(n), get(m), get(x2), get(y2); n += 5; m += 5; x2 += 5; y2 += 5; dp[5][5] = 1; dp[x2][y2] = -1; dp[x2+2][y2+1] = -1; dp[x2+2][y2-1] = -1; dp[x2-2][y2+1] = -1; dp[x2-2][y2-1] = -1; dp[x2+1][y2+2] = -1; dp[x2+1][y2-2] = -1; dp[x2-1][y2+2] = -1; dp[x2-1][y2-2] = -1; for (int i = 6; i <= m; i++) { if (dp[5][i] == 0) dp[5][i] = dp[5][i-1]; else dp[5][i] = 0; } for (int i = 6; i <= n; i++) { if (dp[i][5] == 0) dp[i][5] = dp[i-1][5]; else dp[i][5] = 0; } for (int i = 6; i <= n; i++) for (int j = 6; j <= m; j++) { if (dp[i][j] == 0) dp[i][j] = dp[i-1][j] + dp[i][j-1]; else dp[i][j] = 0; } put(dp[n][m]); return 0; }
区间型
区间DP的简单思路:每个区间的最优值都是由比它小的区间相加得到的,就这样不断划分到最小的区间,是一种分治。下面看一下伪代码吧。
/* 定义dp[i][j]为从i~j数据相加的最小代价, 初始化dp[i][i]为0(单个区间无法合并),每 次使用k(i<= k <= j -1)将区间分为两个部 分来计算。 */ for (int p = 2; p <= n; p++)//p为区间长度,n为最大长度 { for (int i = 1; i <= n-p+1; i++)//i是枚举起点 { int j = i + p - 1;//j为枚举终点 dp[i][j] = INF;//若是求代价最大值则初值为-INF for (int k = i; k <= j - 1; k++)//进行状转 dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + w[i]) } }
看例题吧。
Codevs 1048石子归并
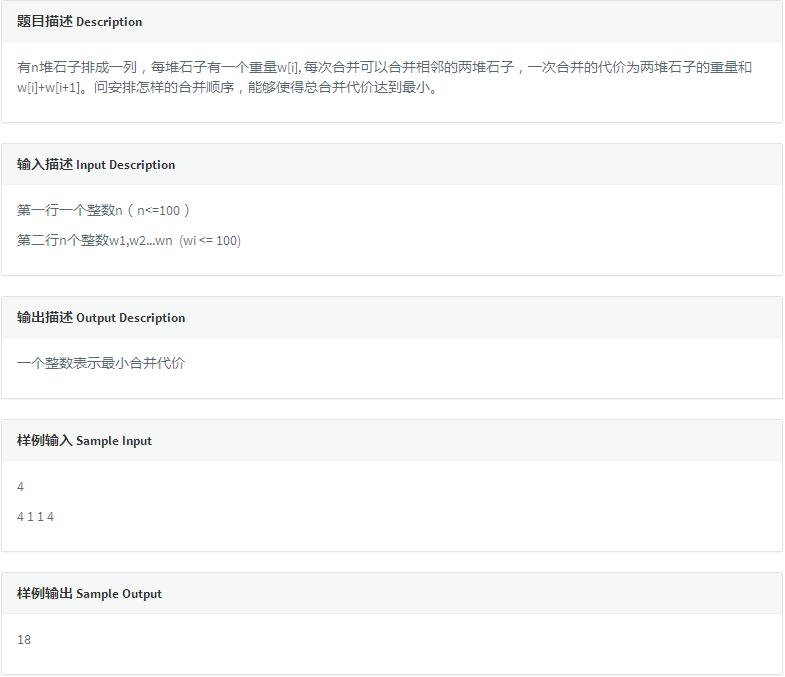
一道很经典也很裸的区间DP,对于数据的处理,我们可以设置的一前缀和数组来存石子的权值,因为石子合并永远是按11合并,22合并,33合并...nn合并形式进行的,用前缀和会比较方便。根据题意写出状转方程dp[i][j]=min{dp[i][j], dp[i][k] + dp[k+1][j] + w[i]},其中w[i]为s[j] - s[i]。
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define oo 0x7f7f7f7f #define get(x) scanf("%d", &x) #define put(x) printf("%d", x) #define cln(x) memset(x, 0, sizeof(x)) using namespace std; int n; int s[110]; int dp[110][110]; int main() { get(n); for (int i = 1; i <= n; i++) { int w; get(w); s[i] = s[i-1] + w; } for (int p = 2; p <= n; p++) { for (int i = 1; i <= n-p+1; i++) { int j = i + p - 1; dp[i][j] = oo; for (int k = i; k <= j-1; k++) { dp[i][j] = min(dp[i][j], dp[i][k] + dp[k+1][j] + s[j] - s[i-1]); } } } put(dp[1][n]); return 0; }
可以看出和模板没啥区别。
划分型
划分型DP很多地方和区间DP很像,也就不多赘述了,上一道例题吧
Codevs 1017乘积最大

思路:设置一个二维数组a,a[i][j]表示从第i位到第j位所表示的数,dp[i][j]表示前i个数划分j次的最大值。就像下图那样( a == mul )
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define oo 0x7f7f7f7f #define lnt long long #define get(x) scanf( "%d", &x ) #define put(x) printf( "%d", x ) #define set( x, y ) memset( x, y, sizeof(x) ) using namespace std; int n, k, res; int a[45][10]; int dp[45][10]; char str[45]; int num( char x ) { return ( int(x) - 48 ); } int main() { get(n), get(k); scanf( "%s", str+1 ); set( dp, -1 ); for ( int i = 1; i <= n; i++ ) { for ( int j = 1; j <= n; j++ ) { res = 0; for ( int k = i; k <= j; k++ ) res = res * 10 + str[k] - 48; a[i][j] = res; } } for ( int i = 1; i <= n; i++ ) dp[i][0] = a[1][i]; for ( int j = 1; j <= k; j++ ) for ( int i = j+1; i <= n; i++ ) for ( int k = j; k <= i; k++ ) dp[i][j] = max( dp[i][j], dp[k][j-1] * a[k+1][i] ); cout << dp[n][k]; return 0; }