数学基础：HDU2802-F(N)（寻找循环节）

F(N)

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5062 Accepted Submission(s): 1805

Problem Description

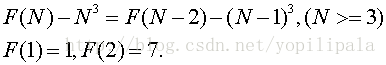
Giving the N, can you tell me the answer of F(N)?

Input

Each test case contains a single integer N(1<=N<=10^9). The input is terminated by a set starting with N = 0. This set should not be processed.

Output

For each test case, output on a line the value of the F(N)%2009.

Sample Input

1
2
3
0

Sample Output

1
7
20

---

解题心得：

1. 这个题就是叫你找一个循环节，为什么是循环节呢，首先这个题暴力是没有可能的，不是等差数列，等比数列，以及一些特殊的数列，就只能够往循环节这方面想了。但是这个循环节也有一个小的坑点，在找循环节的时候并不能够找到等于第一个数就停止，要找到这个数与第二个数相同并且它的前一个数和第一个数相同才能够跳出（就本题来说循环节是4018），为啥呢？因为这个题数列是从第一个和第二个数开始的，如果仅仅只是找到和第一个数相同但是第二个数不同，那么得到的仍然是不同的数列。在找循环节的时候一定要看清楚在那种情况下才能循环，看是怎么开始得到的数列，不然很可能找到错误的答案。
2. 在找循环节的相关问题的时候，为了保险起见可以在找寻环节的时候打一个表，用肉眼看看是否真的是循环，别弄错了。

---

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5000;
const int mod = 2009;
typedef long long ll;
ll num[maxn];
int main()
{
    int t =3;
    num[1] = 1;
    num[2] = 7;
    for(int i=3;i<5000;i++)
    {
        long long k = 3*i*i - 3*i + 1;
        k %= mod;
        ll now = (num[i-2] + k)%mod;
        if(now == num[2] && num[i-1] == num[1])//找到起点了就跳出
            break;
        num[t++] = now;
    }
    t-=2;//这里要减去找到的超出的两个数
    ll n;
    while(scanf("%lld",&n) && n)
    {
        n = n % t;
        if(n == 0)//当是0的时候就是找在了末尾的一个数上面
            printf("%lld
",num[t]);
        else
            printf("%lld
",num[n]);
    }
    return 0;
}