这篇文章的核心思想就是:
要让读者在不看任何数学公式的情况下理解傅里叶分析。
傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多大一新生上来就懵圈并从此对它深恶痛绝。老实说,这么有意思的东西居然成了大学里的杀手课程,不得不归咎于编教材的人实在是太严肃了。(您把教材写得好玩一点会死吗?会死吗?)所以我一直想写一个有意思的文章来解释傅里叶分析,有可能的话高中生都能看懂的那种。所以,不管读到这里的您从事何种工作,我保证您都能看懂,并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友,也希望不要看到会的地方就急忙往后翻,仔细读一定会有新的发现。
————以上是定场诗————
下面进入正题:
抱歉,还是要啰嗦一句:其实学习本来就不是易事,我写这篇文章的初衷也是希望大家学习起来更加轻松,充满乐趣。但是千万!千万不要把这篇文章收藏起来,或是存下地址,心里想着:以后有时间再看。这样的例子太多了,也许几年后你都没有再打开这个页面。无论如何,耐下心,读下去。这篇文章要比读课本要轻松、开心得多……
一、嘛叫频域
从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。
先举一个公式上并非很恰当,但意义上再贴切不过的例子:
在你的理解中,一段音乐是什么呢?
这是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对于乐器小能手们来说,音乐更直观的理解是这样的:

好的!下课,同学们再见。
是的,其实这一段写到这里已经可以结束了。上图是音乐在时域的样子,而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生,只是从来没意识到而已。
现在我们可以回过头来重新看看一开始那句痴人说梦般的话:世界是永恒的。
将以上两图简化:
时域:
频域:

在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。
所(前方高能!~~~~~~~~~~~非战斗人员退散~~~~~~~)
以(~~~~~~~~~~~~~~~前方高能预警~~~~~~~~~~~~~~前方高能~~~~~~~~)
你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。
(众人:鸡汤滚出知乎!)
抱歉,这不是一句鸡汤文,而是黑板上确凿的公式:傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正弦波的叠加。在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。
而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation),我们从简单的开始谈起。
二、傅里叶级数(Fourier Series)
还是举个栗子并且有图有真相才好理解。
如果我说我能用前面说的正弦曲线波叠加出一个带 90 度角的矩形波来,你会相信吗?你不会,就像当年的我一样。但是看看下图:
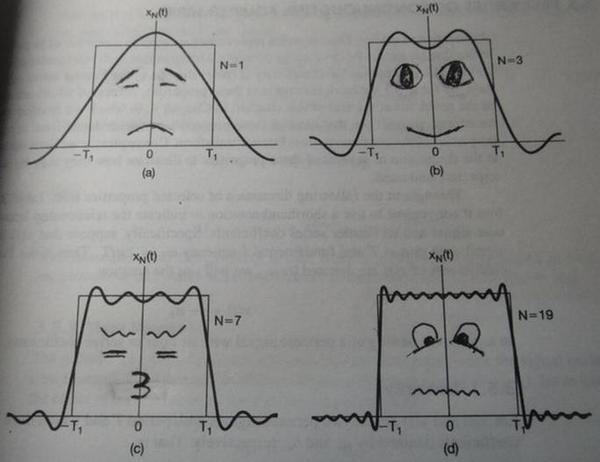
第一幅图是一个郁闷的正弦波 cos(x)
第二幅图是 2 个卖萌的正弦波的叠加 cos(x)+a.cos(3x)
第三幅图是 4 个发春的正弦波的叠加
第四幅图是 10 个便秘的正弦波的叠加
随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,大家从中体会到了什么道理?
(只要努力,弯的都能掰直!)
随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢?不幸的告诉大家,答案是无穷多个。(上帝:我能让你们猜着我?)
不仅仅是矩形,你能想到的任何波形都是可以如此方法用正弦波叠加起来的。这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。
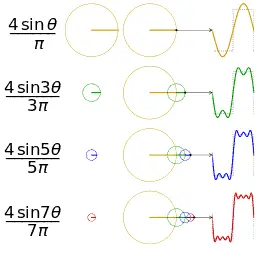
还是上图的正弦波累加成矩形波,我们换一个角度来看看:
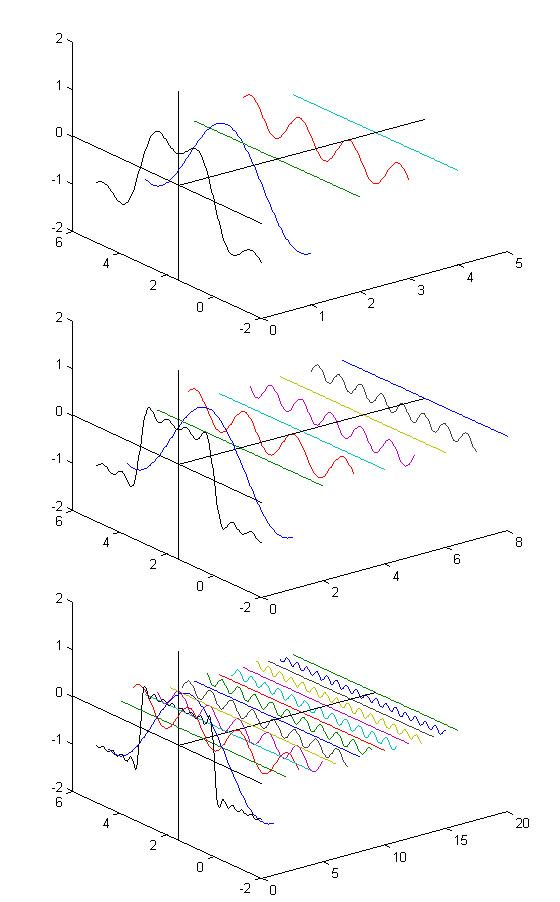
在这几幅图中,最前面黑色的线就是所有正弦波叠加而成的总和,也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。这些正弦波按照频率从低到高从前向后排列开来,而每一个波的振幅都是不同的。一定有细心的读者发现了,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。
这里,不同频率的正弦波我们成为频率分量。
好了,关键的地方来了!!
如果我们把第一个频率最低的频率分量看作“1”,我们就有了构建频域的最基本单元。
对于我们最常见的有理数轴,数字“1”就是有理数轴的基本单元。
(好吧,数学称法为——基。在那个年代,这个字还没有其他奇怪的解释,后面还有正交基这样的词汇我会说吗?)
时域的基本单元就是“1 秒”,如果我们将一个角频率为
的正弦波 cos(
t)看作基础,那么频域的基本单元就是
。
有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0 频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
接下来,让我们回到初中,回忆一下已经死去的八戒,啊不,已经死去的老师是怎么定义正弦波的吧。
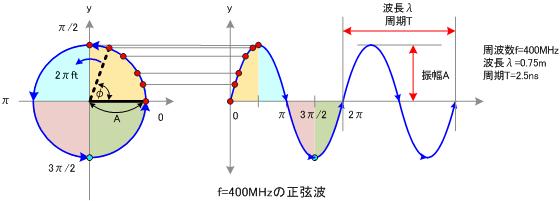
正弦波就是一个圆周运动在一条直线上的投影。所以频域的基本单元也可以理解为一个始终在旋转的圆
知乎不能传动态图真是太让人惋惜了……
想看动图的同学请戳这里:
File:Fourier series square wave circles animation.gif
以及这里:
File:Fourier series sawtooth wave circles animation.gif
点出去的朋友不要被 wiki 拐跑了,wiki 写的哪有这里的文章这么没节操是不是。
介绍完了频域的基本组成单元,我们就可以看一看一个矩形波,在频域里的另一个模样了:
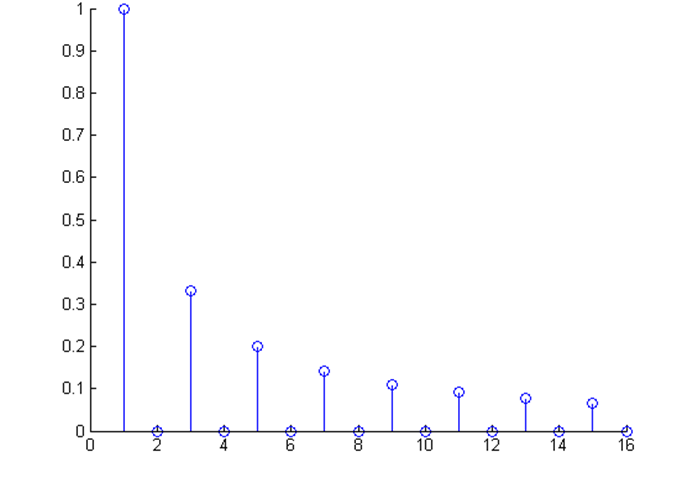
这是什么奇怪的东西?
这就是矩形波在频域的样子,是不是完全认不出来了?教科书一般就给到这里然后留给了读者无穷的遐想,以及无穷的吐槽,其实教科书只要补一张图就足够了:频域图像,也就是俗称的频谱,就是——
再清楚一点:
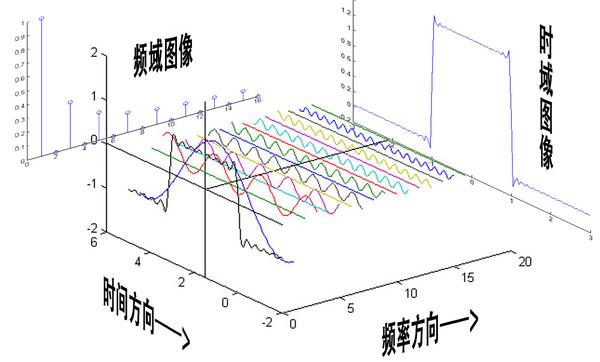
可以发现,在频谱中,偶数项的振幅都是 0,也就对应了图中的彩色直线。振幅为 0 的正弦波。
动图请戳:
File:Fourier series and transform.gif
老实说,在我学傅里叶变换时,维基的这个图还没有出现,那时我就想到了这种表达方法,而且,后面还会加入维基没有表示出来的另一个谱——相位谱。
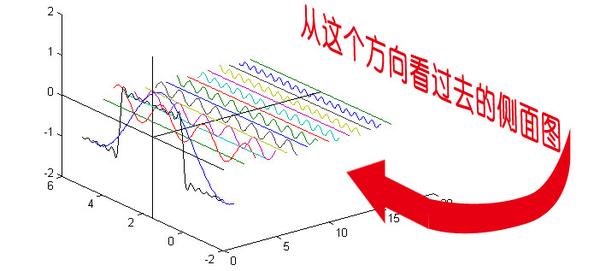
但是在讲相位谱之前,我们先回顾一下刚刚的这个例子究竟意味着什么。记得前面说过的那句“世界是静止的”吗?估计好多人对这句话都已经吐槽半天了。想象一下,世界上每一个看似混乱的表象,实际都是一条时间轴上不规则的曲线,但实际这些曲线都是由这些无穷无尽的正弦波组成。我们看似不规律的事情反而是规律的正弦波在时域上的投影,而正弦波又是一个旋转的圆在直线上的投影。那么你的脑海中会产生一个什么画面呢?
我们眼中的世界就像皮影戏的大幕布,幕布的后面有无数的齿轮,大齿轮带动小齿轮,小齿轮再带动更小的。在最外面的小齿轮上有一个小人——那就是我们自己。我们只看到这个小人毫无规律的在幕布前表演,却无法预测他下一步会去哪。而幕布后面的齿轮却永远一直那样不停的旋转,永不停歇。这样说来有些宿命论的感觉。说实话,这种对人生的描绘是我一个朋友在我们都是高中生的时候感叹的,当时想想似懂非懂,直到有一天我学到了傅里叶级数……
抱歉,还是没写完。但是我想坚持看到这里的人已经很不容易了。我们都休息一下,下一讲再继续……
from: http://daily.zhihu.com/story/3935067