LCA:最近公共祖先
指在有根树中,找出某两个结点u和v最近的公共祖先
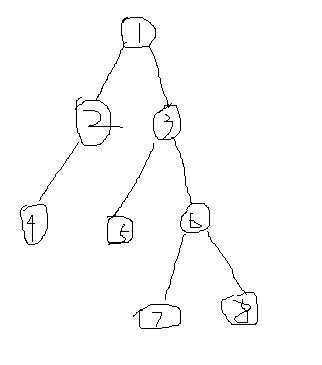
如图,5,7的最近公共祖先就是3
接下来,我们来了解如何求解LCA
No.1 暴力
首先想到的肯定是暴力,我们搜索,从两个节点一步一步向上爬。
待你爬到之时,你自然会感到TLE的魅力
复杂度:O(nm)(最坏)
No.2 倍增法
倍增的主要思想就是,让较深的节点向上爬,爬到和较浅的节点同高度(然后它们就相爱了,不过它优的是,它不是一个一个向上爬
即:先搜一遍树,预处理出x的第(1<=2k<=max(dep))个父亲,存起来.询问时,还是让深度更大的节点x向上倍增至与另一节点y在同一深度上,然后一起倍增向上跳
建树:

求解:

因为涉及倍增,所以倍增法在复杂度方面肯定比暴力更优,降n为logn
复杂度:(mlogn)
No.3 离线tarjan法
我们先将所有询问存起来,DFS一遍的同时我们将已经回溯完的标记为'′1′′,正在dfs的及dfs过但未回溯的标记为''2'
然后在正在dfs的节点中处理与它有关的询问,若正在回溯已经DFS过的节点x,有个询问是求LCA(x,y)。
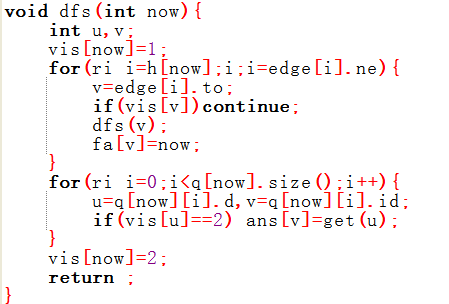
若y的标记是′′1′′,显然y第一个标记为′′2′′的祖先就为LCA(x,y)。
若标记不是''1'',比如当y是x祖宗还是没关系,在回溯到y时,y就是符合要求的答案。
那怎么快速求第一个标记为'′′2′′的祖先呢?用并查集维护一下就好了.
显然,此种方法的复杂度更优。但是,我们容易发现,它只能离线求解,所以它适于数据范围较大且离线操作的题目。
复杂度O(N+M)
No.4 ST法
由欧拉序,经过ST的预处理后,比较大小,小的当作左区间l,大的当作右区间r,之后查询l<=i<=r里面使得deep[i]最小的值,返回对应下标即最近公共祖先。

复杂度:O(n+m+nlogn)
最后的重头戏,恩,,我最喜欢的一种方法(学姐教的
树剖大法:
首先,我们要建树!
在建树的过程中,我们可以求出每个点的深度,每个点的父节点,以及每棵子树的大小。

接下来我们要处理轻链和重链

处理好轻链重链之后,我们可以根据判断它们在那条链上,以便于求解。

复杂度:O(mlogn)
以上干货报道完毕。
以下是代码time:
1.暴力就不发了。
2.倍增:
#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int maxn=500000+2; int n,m,s,k; int head[maxn],deep[maxn],dad[maxn][21]; struct node { int v,next; } e[maxn*2]; void add(int u,int v) { e[k].v=v; e[k].next=head[u]; head[u]=k++; e[k].v=u; e[k].next=head[v]; head[v]=k++; } void dfs(int u,int fa) { deep[u]=deep[fa]+1; dad[u][0]=fa; for(int i=1; (1<<i)<=deep[u]; i++) dad[u][i]=dad[dad[u][i-1]][i-1]; for(int i=head[u]; i!=-1; i=e[i].next) { int v=e[i].v; if(v!=fa) dfs(v,u); } } int lca(int a,int b) { if(deep[a]>deep[b]) swap(a,b); for(int i=20; i>=0; i--) if(deep[a]<=deep[b]-(1<<i)) b=dad[b][i]; if(a==b) return a; for(int i=20; i>=0; i--) { if(dad[a][i]==dad[b][i]) continue; else a=dad[a][i],b=dad[b][i]; } return dad[a][0]; } int main() { memset(head,-1,sizeof(head)); int a,b; scanf("%d%d%d",&n,&m,&s); for(int i=1; i<n; i++) { scanf("%d%d",&a,&b); add(a,b); } dfs(s,0); for(int i=1; i<=m; i++) { scanf("%d%d",&a,&b); printf("%d ",lca(a,b)); } return 0; }
3.离线tarjan
#include <map> #include <queue> #include <cstdio> #include <cctype> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> #define ll long long #define ri register int #define ull unsigned long long using namespace std; const int maxn=500005; const int inf=0x7fffffff; int n,m,s,t; struct Edge{ int ne,to; }edge[maxn<<1]; struct node{ int d,id; node(int x,int y){d=x,id=y;} node(){;} }; vector <node>q[maxn]; int h[maxn],num_edge,ans[maxn]; inline void add_edge(int u,int v){ edge[++num_edge].ne=h[u]; edge[num_edge].to=v; h[u]=num_edge; edge[++num_edge].ne=h[v]; edge[num_edge].to=v; h[v]=num_edge; } int fa[maxn],vis[maxn]; int get(int x){ if(fa[x]!=x)fa[x]=get(fa[x]); return fa[x]; } void dfs(int now){ int u,v; vis[now]=1; for(ri i=h[now];i;i=edge[i].ne){ v=edge[i].to; if(vis[v])continue; dfs(v); fa[v]=now; } for(ri i=0;i<q[now].size();i++){ u=q[now][i].d,v=q[now][i].id; if(vis[u]==2) ans[v]=get(u); } vis[now]=2; return ; } int main(){ int x,y; cin>>n>>m>>s; for(ri i=1;i<n;i++){ cin>>x>>y; add_edge(x,y); fa[i]=i; } fa[n]=n; for(ri i=1;i<=m;i++){ cin>>x>>y; q[x].push_back(node(y,i)); q[y].push_back(node(x,i)); } dfs(s); for(ri i=1;i<=m;i++) printf("%d ",ans[i]); return 0; }
4.ST表
#include<cstdio> #include<iostream> #include<cstring> #include<cmath> #include<algorithm> #include<queue> using namespace std; int n,m,s,x,y,tot,cnt; const int N=500005,M=1000005; int head[N],to[M],nxt[M],deep[M],vis[M],size[M]; int dad[M][20],dis[M]; void add(int x,int y) { to[++tot]=y; nxt[tot]=head[x]; head[x]=tot; to[++tot]=x; nxt[tot]=head[y]; head[x]=tot; } void DFS(int u,int fa,int l) { size[u]=++cnt; vis[cnt]=u; deep[cnt]=l; for(int i=head[u]; i; i=nxt[i]) { int v=to[i]; if(v==fa) continue; DFS(v,u,l+1); vis[++cnt]=u; deep[cnt]=l; } return ; } void RMQ() { for(int i=1; i<=cnt; i++) dis[i]=dis[i-1]+(1<<dis[i-1]==i); for(int i=1; i<=cnt; i++) dad[i][0]=i; for(int i=1; (1<<i)<=cnt; i++) { for(int j=1; j+(1<<i)-1<=cnt; j++) { int a=dad[j][i-1]; int b=dad[j+(1<<(i-1))][i-1]; if(deep[a]<=deep[b]) dad[j][i]=a; else dad[j][i]=b; } } return ; } int ST(int x,int y) { int r=size[x],l=size[y]; if(r<l) swap(r,l); int k=dis[r-l+1]-1,a=dad[l][k],b=dad[r-(1<<k)+1][k]; if(deep[a]<=deep[b]) return vis[a]; else return vis[b]; } int main() { cin>>n>>m>>s; for(int i=1; i<n; i++) { cin>>x>>y; add(x,y); } DFS(s,0,1); RMQ(); for(int i=1; i<=m; ++i) { cin>>x>>y; cout<<ST(x,y); } return 0; }
5.树剖
/* 注释掉的代码是当有边权时的写法 */ #include <algorithm> #include <cstring> #include <cstdio> using namespace std; const int M = 500005; int n, m, tot; int to[M*2], net[M*2], head[M];// cap[M*2]; int deep[M], top[M], size[M], dad[M];//length[M]; void add(int u, int v, int w) { to[++tot] = v; net[tot] = head[u]; head[u] = tot;// cap[tot] = w; to[++tot] = u; net[tot] = head[v]; head[v] = tot;// cap[tot] = w; } void dfs(int now) { //建树 size[now] = 1; deep[now] = deep[dad[now]] + 1; for (int i = head[now]; i; i = net[i]) if (to[i] != dad[now]) { dad[to[i]] = now; // length[to[i]] = length[now] + cap[i]; dfs(to[i]); size[now] += size[to[i]]; } } void dfsl(int now) { //处理轻重链 int t = 0; if (!top[now]) top[now] = now; for (int i = head[now]; i; i = net[i]) //求重儿子 if (to[i] != dad[now] && size[to[i]] > size[t]) t = to[i]; if (t) { //处理重链 top[t] = top[now]; dfsl(t); } for (int i = head[now]; i; i = net[i]) //处理轻链 if (to[i] != dad[now] && to[i] != t) dfsl(to[i]); } int lca(int x, int y) { //求LCA while (top[x] != top[y]) { if (deep[top[x]] < deep[top[y]]) swap(x, y); x = dad[top[x]]; } return deep[x] > deep[y] ? y : x; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i < n; ++i) { //因为树的边有n-1条,所以循环要i<n int u, v; scanf("%d%d", &u, &v); add(u, v); /* int u, v, w; scanf("%d%d%d", &u, &v, &w); add(u, v, w); */ } dfs(1); //一般题目默认根节点为1号节点,如果不是,将这两个dfs括号中的1换为题目中规定的节点即可 dfsl(1); for (int i = 1; i <= m; ++i) { //查询LCA的次数 int u, v; scanf("%d%d", &u, &v); printf("%d ", lca(u, v)); } return 0; }
一世安宁