Day6

Stan and Ollie play the game of Odd Brownie Points. Some brownie points are located in the plane, at integer coordinates. Stan plays first and places a vertical line in the plane. The line must go through a brownie point and may cross many (with the same x-coordinate). Then Ollie places a horizontal line that must cross a brownie point already crossed by the vertical line.
Those lines divide the plane into four quadrants. The quadrant containing points with arbitrarily large positive coordinates is the top-right quadrant.

The players score according to the number of brownie points in the quadrants. If a brownie point is crossed by a line, it doesn't count. Stan gets a point for each (uncrossed) brownie point in the top-right and bottom-left quadrants. Ollie gets a point for each (uncrossed) brownie point in the top-left and bottom-right quadrants.

Stan and Ollie each try to maximize his own score. When Stan plays, he considers the responses, and chooses a line which maximizes his smallest-possible score.

Input

Input contains a number of test cases. The data of each test case appear on a sequence of input lines. The first line of each test case contains a positive odd integer 1 < n < 200000 which is the number of brownie points. Each of the following n lines contains two integers, the horizontal (x) and vertical (y) coordinates of a brownie point. No two brownie points occupy the same place. The input ends with a line containing 0 (instead of the n of a test).

Output

For each input test, print a line of output in the format shown below. The first number is the largest score which Stan can assure for himself. The remaining numbers are the possible (high) scores of Ollie, in increasing order.

Sample Input

11
3 2
3 3
3 4
3 6
2 -2
1 -3
0 0
-3 -3
-3 -2
-3 -4
3 -7
0

Sample Output

Stan: 7; Ollie: 2 3;

简述一下题意，给你一些点的x，y坐标，过一点做垂线，再做一条水平线，且该水平线必须经过已经被第一条垂线穿过的点，将所有点分成了4份，Stan是左下右上点个数之和，Ollie是左上右下，
求出Stan的值，使其最小值最大，并且输出该条垂线下，Stan取该值时，Ollie值的最大值，升序打印。
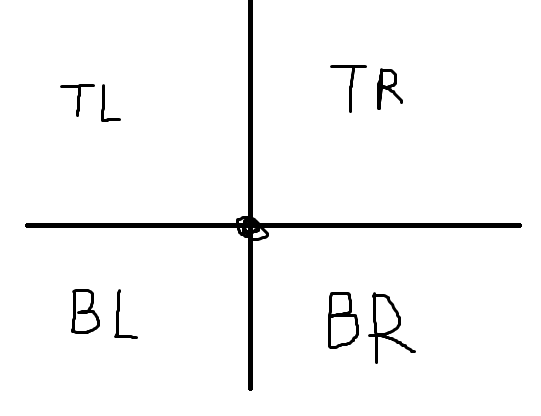
思路：读题意，求个数之和，想到二维树状数组，看数据范围，变成偏序问题，离散化后一维树状数组即可，本题的细节主要是在如何求这四份，树状数组可以求出左下区域，那么就分别维护每个点上下左右各有多少点，结合左下就可以求出其他区域，如图：

TL = 该点左侧的点-BL， TR = 该点上侧的点-TL, BR = 该点右侧的点-TR

细节代码中有注释(补到线段树和扫描线再做一次

using namespace std;
#define lowbit(x) ((x)&(-x))
typedef long long LL;

const int maxm = 2e5+5;
const int INF = 0x3f3f3f3f;

int x[maxm], y[maxm], numx[maxm], numy[maxm], Left[maxm], Right[maxm], 
Upper[maxm], Lower[maxm], n, totx, toty, C[maxm], ally[maxm], allx[maxm], 
sumLeft[maxm], sumRight[maxm], sumUpper[maxm], sumLower[maxm], sumx[maxm], sumy[maxm], 
ans1[maxm], ans2[maxm];
bool vis[maxm];

void init() {
    totx = toty = 0;
    memset(ans1, 63, sizeof(ans1)), memset(ans2, -1, sizeof(ans2));
    memset(C, 0, sizeof(C)), memset(numx, 0, sizeof(numx)), memset(numy, 0, sizeof(numy));
    memset(sumx, 0, sizeof(sumx)), memset(sumy, 0, sizeof(sumy)), memset(vis, 0, sizeof(vis));
}

void add(int pos, int val) {
    for(; pos <= toty; pos += lowbit(pos))
        C[pos] += val;
}

int getsum(int pos) {
    int ret = 0;
    for(; pos; pos -= lowbit(pos))
        ret += C[pos];
    return ret;
}

struct Node {
    int x, y;
    Node(){}
    bool operator<(const Node &a) const {
        return x < a.x || (x == a.x && y < a.y);
    }
} Nodes[maxm];

int main() {
    while(scanf("%d", &n) && n) {
        init();
        // 读入并对x,y离散化
        for(int i = 1; i <= n; ++i) {
            scanf("%d%d", &x[i], &y[i]);
            allx[++totx] = x[i], ally[++toty] = y[i];
        }
        sort(allx+1, allx+1+totx), sort(ally+1,ally+1+toty);
        int lenx = unique(allx+1, allx+1+totx)-allx-1, leny = unique(ally+1,ally+1+toty)-ally-1;
        int nodenum = 0;
        for(int i = 1; i <= n; ++i) {
            Nodes[++nodenum].x = lower_bound(allx+1,allx+lenx+1, x[i]) - allx;
            Nodes[nodenum].y = lower_bound(ally+1,ally+leny+1, y[i]) - ally;
        }
        sort(Nodes+1, Nodes+nodenum+1);
        // 求出每个点上下左右垂直有多少个点
        for(int i = 1; i <= nodenum; ++i) {
            Lower[i] = numx[Nodes[i].x]++;
            Left[i] = numy[Nodes[i].y]++;
        }
        for(int i = 1; i <= nodenum; ++i) {
            Upper[i] = numx[Nodes[i].x] - Lower[i] - 1;
            Right[i] = numy[Nodes[i].y] - Left[i] - 1;
        }
        // 求出坐标xi=1,2,的左侧 yi=1,2,的下侧 一共有多少个点 水平/垂直线(包括该线)
        for(int i = 1; i <= lenx; ++i) {
            sumx[i] = sumx[i-1] + numx[i];
        }
        for(int i = 1; i <= leny; ++i) {
            sumy[i] = sumy[i-1] + numy[i];
        }
        // 计算每个点上下左右侧一共有几个点
        for(int i = 1; i <= nodenum; ++i) {
            int x = Nodes[i].x, y = Nodes[i].y;
            sumLeft[i] = sumx[x-1];
            sumRight[i] = sumx[lenx] - sumx[x];
            sumLower[i] = sumy[y-1];
            sumUpper[i] = sumy[leny] - sumy[y];
        }
        for(int i = 1; i <= nodenum; ++i) {
            int x = Nodes[i].x, y = Nodes[i].y;
            int BL = getsum(y-1) - Lower[i];
            int TL = sumLeft[i] - BL - Left[i];
            int TR = sumUpper[i] - TL - Upper[i];
            int BR = sumLower[i] - BL - Lower[i];
            add(y, 1);
            if(BL + TR < ans1[x]) {
                ans1[x] = BL + TR, ans2[x] = TL + BR;
            } else if(BL + TR == ans1[x]) ans2[x] = max(ans2[x], TL + BR);
        }
        int ans = 0;
        for(int i = 1; i <= lenx; ++i)
            if(ans1[i] < INF)
                ans = max(ans, ans1[i]);
        printf("Stan: %d; Ollie:",ans);
        for(int i = 1; i <= lenx; ++i)
            if(ans1[i] == ans) vis[ans2[i]] = true;
        for(int i = 0; i <= n; ++i)
            if(vis[i])
                printf(" %d", i);
        printf(";
");
    }
}