牛客网暑期ACM多校训练营（第五场）A-gap (二分答案）

题目描述
给定n 门课以及它们的学分和绩点，定义总绩点是所有课的加权平均数，给定一个数k，
你可以删除最多k 门课，求你的总绩点最大能到多少
1 <=n <=10^5

解题思路
考虑分数规划
二分答案，假设当前二分了一个值D，我们要判断是否存在一个方案使得总绩点>=D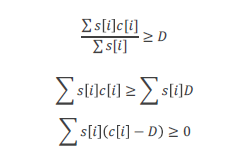

于是选前k 个最小的删了就行了
时间复杂度：O(nlogn)

什么是二分答案：

适用范围：二分答案的做法适用于题目答案满足某种意义上的单调性，直接求解难以接受，并且验证解是否可行较为容易的题目，常见的模型有“求xx的最值”“求最少/多需要多少xx才能满足xx”等。而二分的模型增加的时间复杂度只有log(区间长度)，基本可以接受。

时间复杂度：logn.

如果暴力枚举，那么会做许多无用功。我们来设想一下。同样假设答案是上界，如果我们check了10000，发现它是满足解的，那么答案肯定不小于10000。如果我们又check了 20000，发现它是满足解的，那么10000~20000内的数我们都不用枚举。又或者20000是不满足解的，那么答案就在10000~20000的 左闭右开区间内。这个时候我们如果”恰当地“check 15000，答案的范围会进一步缩小。

代码：

#include<cstdio>
#include<algorithm>
#define M ((L+R)/2)
using namespace std;

int s[100005],c[100005],n,k;
double L,R,t[100005];

bool check(double x)
{
    for(int i=1;i<=n;i++)
        t[i]=s[i]*(c[i]-x);
    sort(t+1,t+n+1);
    double tmp=0;
    for(int i=k+1;i<=n;i++)
        tmp+=t[i];
    return tmp>0;
}

int main()
{
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++)
        scanf("%d",&s[i]);
    for(int i=1;i<=n;i++)
        scanf("%d",&c[i]),R=max(R,(double)c[i]);
    while(R-L>1e-7)
        if(check(M))
            L=M;
        else
            R=M;
    printf("%.10lf",R);
    return 0;
}