昨天做了一个求[1,n]里能被[2,m]中的数整除的个数,就去搜容斥原理,找到一篇讲得特别好的博客,就转载了其中一部分过来。
转载:https://blog.csdn.net/m0_37286282/article/details/78869512
关于集合的原理公式
上述描述的公式形式可以表示如下:
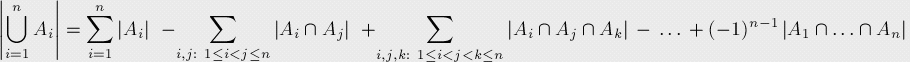
它可以写得更简洁一些,我们将B作为所有Ai的集合,那么容斥原理就变成了:
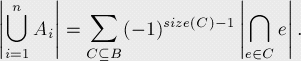
这个公式是由 De Moivre (Abraham de Moivre)提出的。
关于概率论的原理
设事件![]() ,
,![]() 代表发生某些事件的概率(即发生其中至少一个事件的概率),则:
代表发生某些事件的概率(即发生其中至少一个事件的概率),则:
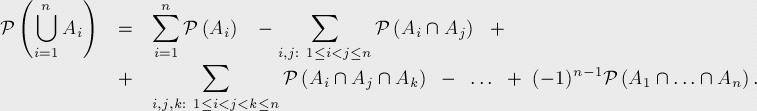
这个公式也可以用B代表Ai的集合:
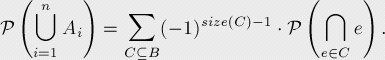
对于实际问题的应用
一个简单的排列问题
由0到9的数字组成排列,要求第一个数大于1,最后一个数小于8,一共有多少种排列?
我们可以来计算它的逆问题,即第一个元素<=1或者最后一个元素>=8的情况。
我们设第一个元素<=1时有X组排列,最后一个元素>=8时有Y组排列。那么通过容斥原理来解决就可以写成:
![]()
经过简单的组合运算,我们得到了结果:
![]()
然后被总的排列数10!减,就是最终的答案了。
(0,1,2)序列问题
长度为n的由数字0,1,2组成的序列,要求每个数字至少出现1次,这样的序列有多少种?
同样的,我们转向它的逆问题。也就是不出现这些数字的序列 不出现其中某些数字的序列。
我们定义Ai(i=0…2)表示不出现数字i的序列数,那么由容斥原理,我们得到该逆问题的结果为:
![]()
可以发现每个Ai的值都为2^n(因为这些序列中只能包含两种数字)。而所有的两两组合![]() 都为1(它们只包含1种数字)。最后,三个集合的交集为0。(因为它不包含数字,所以不存在)
都为1(它们只包含1种数字)。最后,三个集合的交集为0。(因为它不包含数字,所以不存在)
要记得我们解决的是它的逆问题,所以要用总数减掉,得到最终结果:
![]()
方程整数解问题
给出一个方程:
![]()
其中![]() 。
。
求这个方程的整数解有多少组。
我们先不去理会xi<=8的条件,来考虑所有正整数解的情况。这个很容易用组合数来求解,我们要把20个元素分成6组,也就是添加5块“夹板”,然后在25个位置中找5块“夹板”的位置。
![]()
然后通过容斥原理来讨论它的逆问题,也就是x>=9时的解。
我们定义Ak为xk>=9并且其他xi>=0时的集合,同样我们用上面的添加“夹板”法来计算Ak的大小,因为有9个位置已经被xk所利用了,所以:
![]()
然后计算两个这样的集合Ak、Ap的交集:
![]()
因为所有x的和不能超过20,所以三个或三个以上这样的集合时是不能同时出现的,它们的交集都为0。最后我们用总数剪掉用容斥原理所求逆问题的答案,就得到了最终结果:
![]()
求指定区间内与n互素的数的个数:
给出整数n和r。求区间[1;r]中与n互素的数的个数。
去解决它的逆问题,求不与n互素的数的个数。
考虑n的所有素因子pi(i=1…k)
在[1;r]中有多少数能被pi整除呢?它就是:
![]()
然而,如果我们单纯将所有结果相加,会得到错误答案。有些数可能被统计多次(被好几个素因子整除)。所以,我们要运用容斥原理来解决。
我们可以用2^k的算法求出所有的pi组合,然后计算每种组合的pi乘积,通过容斥原理来对结果进行加减处理。
关于此问题的最终实现:
1 int solve (int n, int r) { 2 vector<int> p; 3 for (int i=2; i*i<=n; ++i) 4 if (n % i == 0) { 5 p.push_back (i); 6 while (n % i == 0) 7 n /= i; 8 } 9 if (n > 1) 10 p.push_back (n); 11 int sum = 0; 12 for (int msk=1; msk<(1<<p.size()); ++msk) { 13 int mult = 1,bits = 0; 14 for (int i=0; i<(int)p.size(); ++i) 15 if (msk & (1<<i)) { 16 ++bits; 17 mult *= p[i]; 18 } 19 int cur = r / mult; 20 if (bits % 2 == 1) 21 sum += cur; 22 else 23 sum -= cur; 24 } 25 return r - sum; 26 } 27
算法的复杂度为 ![]() 。
。
求在给定区间内,能被给定集合至少一个数整除的数个数
给出n个整数ai和整数r。求在区间[1;r]中,至少能被一个ai整除的数有多少。
解决此题的思路和上题差不多,计算ai所能组成的各种集合(这里将集合中ai的最小公倍数作为除数)在区间中满足的数的个数,然后利用容斥原理实现加减。
此题中实现所有集合的枚举,需要2^n的复杂度,求解lcm需要O(nlogr)的复杂度。