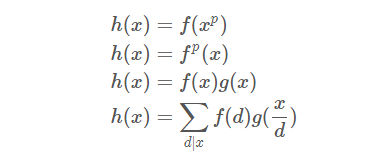莫比乌斯反演的应用范围
一些函数很难直接求值,而容易求出其倍数和或约数和,那么可以通过莫比乌斯反演求得原函数的值。
积性函数
定义:若 gcd(x,y)=1 ,且 f(xy)=f(x)f(y),则 f(n) 为积性函数。
性质:若 f(x) 和 g(x) 均为积性函数,则以下函数也为积性函数。
常见积性函数
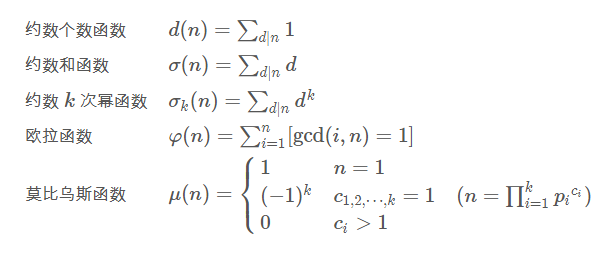
Dirichlet 卷积

- Dirichlet 卷积满足交换律、结合律、分配律。
其中 ε 为 Dirichlet 卷积的单位元(任何函数卷 ε 都为其本身)。

莫比乌斯函数
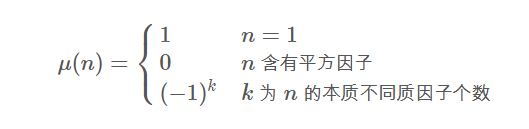

其中最重要的性质就是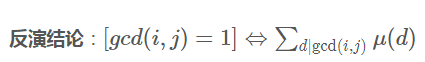
void get_mu(int n){
mu[1]=1; for(int i=2;i<=n;i++){
if(!vis[i]) primes[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&primes[j]*i<=n;j++){
vis[primes[j]*i]=1;
if(i%primes[j]==0) break;
else mu[i*primes[j]]=-mu[i];
}
}
}
莫比乌斯反演

- 公式可以进一步转化为:
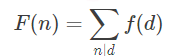
相关习题练习
T1:【p3455】ZAP / 【p4450】双亲数

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//【p3455】ZAP
// 求∑(i=1~n)∑(j=1~m)[gcd(x,y)=d]
// 设f(d)为 gcd(i,j)=d 的个数,F(n)为 gcd(i,j)=d和d的倍数 的个数。
// 即:f(d)=∑(i=1~n)∑(j=1~m)[gcd(i,j)=d],F(n)=∑(n|d)f(d)=⌊N/n⌋⌊M/n⌋。
// 则可以得到:f(n)=∑(n|d) μ(⌊d/n⌋)*F(d)。
// 接下来的推导公式见:http://www.cnblogs.com/peng-ym/p/8652288.html
const int N=10000019;
bool vis[N]; int primes[N],cnt=0,mu[N],g[N]; ll sum[N];
void get_mu(int n){
mu[1]=1; for(int i=2;i<=n;i++){
if(!vis[i]) primes[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&primes[j]*i<=n;j++){
vis[primes[j]*i]=1;
if(i%primes[j]==0) break;
else mu[i*primes[j]]=-mu[i];
}
} for(int i=1;i<=n;i++) sum[i]=sum[i-1]+mu[i];
}
int main(){
int T,n,m,d; cin>>T; get_mu(50000);
while(T--){
scanf("%d%d%d",&n,&m,&d); n=n/d,m=m/d;
ll ans=0; for(int l=1,r;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l)); //整除分块
ans+=1LL*(n/l)*(m/l)*(sum[r]-sum[l-1]);
} cout<<ans<<endl; //满足gcd(x,y)=d的(x,y)对数
}
}
T2:【p2522】problem B
- ZAP+简单容斥原理(类似于二维前缀和的容斥):
ans=Ans((1,b),(1,d))−Ans((1,b),(1,c−1))−Ans((1,a−1),(1,d))+Ans((1,a−1),(1,c−1))

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//【p2522】problem B //'ZAP'的一般情况:求∑(i=a~b)∑(j=c~d)[gcd(x,y)=k]
// 设f(d)为 gcd(i,j)=d 的个数,F(n)为 gcd(i,j)=d和d的倍数 的个数。
// 即:f(d)=∑(i=1~n)∑(j=1~m)[gcd(i,j)=d],F(n)=∑(n|d)f(d)=⌊N/n⌋⌊M/n⌋。
// 则可以得到:f(n)=∑(n|d) μ(⌊d/n⌋)*F(d)。
// ZAP+简单容斥原理即可(类似于二维前缀和的容斥):
// ans=Ans((1,b),(1,d))−Ans((1,b),(1,c−1))−Ans((1,a−1),(1,d))+Ans((1,a−1),(1,c−1))
const int N=10000019;
bool vis[N]; int primes[N],cnt=0,mu[N],k; ll sum[N];
void get_mu(int n){
mu[1]=1; for(int i=2;i<=n;i++){
if(!vis[i]) primes[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&primes[j]*i<=n;j++){
vis[primes[j]*i]=1;
if(i%primes[j]==0) break;
else mu[i*primes[j]]=-mu[i];
}
} for(int i=1;i<=n;i++) sum[i]=sum[i-1]+mu[i];
}
ll calc(int n,int m){ n=n/k,m=m/k;
ll ans=0; for(int l=1,r;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l)); //整除分块
ans+=1LL*(n/l)*(m/l)*(sum[r]-sum[l-1]);
} return ans; //1~n,1~m,满足gcd(x,y)=k的(x,y)对数
}
int main(){ int T,a,b,c,d; cin>>T; get_mu(50000);
while(T--){ scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
cout<<calc(b,d)-calc(b,c-1)-calc(a-1,d)+calc(a-1,c-1)<<endl; } }
T3:【p2257】YY的GCD
- 给定N, M,求1<=x<=N, 1<=y<=M且gcd(x,y)为质数的(x,y)有多少对。

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//【p2257】YY的GCD
// 给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对。
// ∑(i=1~n)∑(j=1~m)[gcd(x,y)=primes]
// 设f(d)为 gcd(i,j)=d 的个数,F(n)为 gcd(i,j)=d和d的倍数 的个数。
// 即:f(d)=∑(i=1~n)∑(j=1~m)[gcd(i,j)=d],F(n)=∑(n|d)f(d)=⌊N/n⌋⌊M/n⌋。
// 则可以得到:f(n)=∑(n|d) μ(⌊d/n⌋)*F(d)。
// 接下来的推导公式见:http://www.cnblogs.com/peng-ym/p/8652288.html
const int N=10000019;
bool vis[N]; int primes[N],cnt=0,mu[N],g[N]; ll sum[N];
void get_mu(int n){
mu[1]=1; for(int i=2;i<=n;i++){
if(!vis[i]) primes[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&primes[j]*i<=n;j++){
vis[primes[j]*i]=1;
if(i%primes[j]==0) break;
else mu[i*primes[j]]=-mu[i];
}
} for(int j=1;j<=cnt;j++)
for(int i=1;i*primes[j]<=n;i++) g[i*primes[j]]+=mu[i];
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+(ll)g[i];
}
int main(){
int T,n,m; cin>>T; get_mu(10000000);
while(T--){
scanf("%d%d",&n,&m); if(n>m) swap(n,m);
ll ans=0; for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l)); //整除分块
ans+=1LL*(n/l)*(m/l)*(sum[r]-sum[l-1]);
} cout<<ans<<endl; //满足gcd(x,y)为质数的(x,y)对数
}
}
T4:【p3327】约数个数和

#include <cmath>
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
//【p3327】约数个数和 // 设d(x)为x的约数个数,求 ∑(i=1~n)∑(j=1~m)d(i*j)
// 约数个数的公式:d(i*j)=∑(x|i)∑(y|j)[gcd(x,y)=1]。
// 设f(d)为 gcd(i,j)=d 的个数,F(n)为 gcd(i,j)=d和d的倍数 的个数。
// 即:f(d)=∑(i=1~n)∑(j=1~m)[gcd(i,j)=d],F(n)=∑(n|d)f(d)=⌊N/n⌋⌊M/n⌋。
// 则可以得到:f(n)=∑(n|d) μ(⌊d/n⌋)*F(d)。
// Ans=∑(i=1~n)∑(j=1~m)∑(x|i)∑(y|j)[gcd(x,y)=1]。
// 根据公式推出:Ans=∑(i=1~n)∑(j=1~m)∑(x|i)∑(y|j)∑(d|gcd(x,y))μ(d)。
// 后续推导见:https://www.cnblogs.com/peng-ym/p/8667321.html。
const int N=10000019;
bool vis[N]; int primes[N],cnt=0,mu[N],g[N]; ll sum[N];
void get_mu(int n){
mu[1]=1; for(int i=2;i<=n;i++){
if(!vis[i]) primes[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&primes[j]*i<=n;j++)
{ vis[primes[j]*i]=1;
if(i%primes[j]==0) break;
else mu[i*primes[j]]=-mu[i]; }
} for(int i=1;i<=n;i++) sum[i]=sum[i-1]+mu[i];
for(int i=1;i<=n;i++){
ll anss=0; for(int l=1,r;l<=i;l=r+1)
r=(i/(i/l)),anss+=1LL*(r-l+1)*(i/l); g[i]=anss;
}
}
int main(){
int T,n,m; cin>>T; get_mu(50000);
while(T--){ scanf("%d%d",&n,&m);
ll ans=0; for(int l=1,r;l<=min(n,m);l=r+1){
r=min(n/(n/l),m/(m/l)); //整除分块
ans+=1LL*g[n/l]*1LL*g[m/l]*(sum[r]-sum[l-1]);
} cout<<ans<<endl; //满足gcd(x,y)=d的(x,y)对数
}
}
- 约数个数的公式:d(i*j)=∑(x|i)∑(y|j)[gcd(x,y)=1]