Codeforces Round #647 (Div. 2)

已给出A,B,C,D,E题解,F待补。（持续补题...）

------------------------------------------------------------------------------------------------------------------

A. Johnny and Ancient Computer

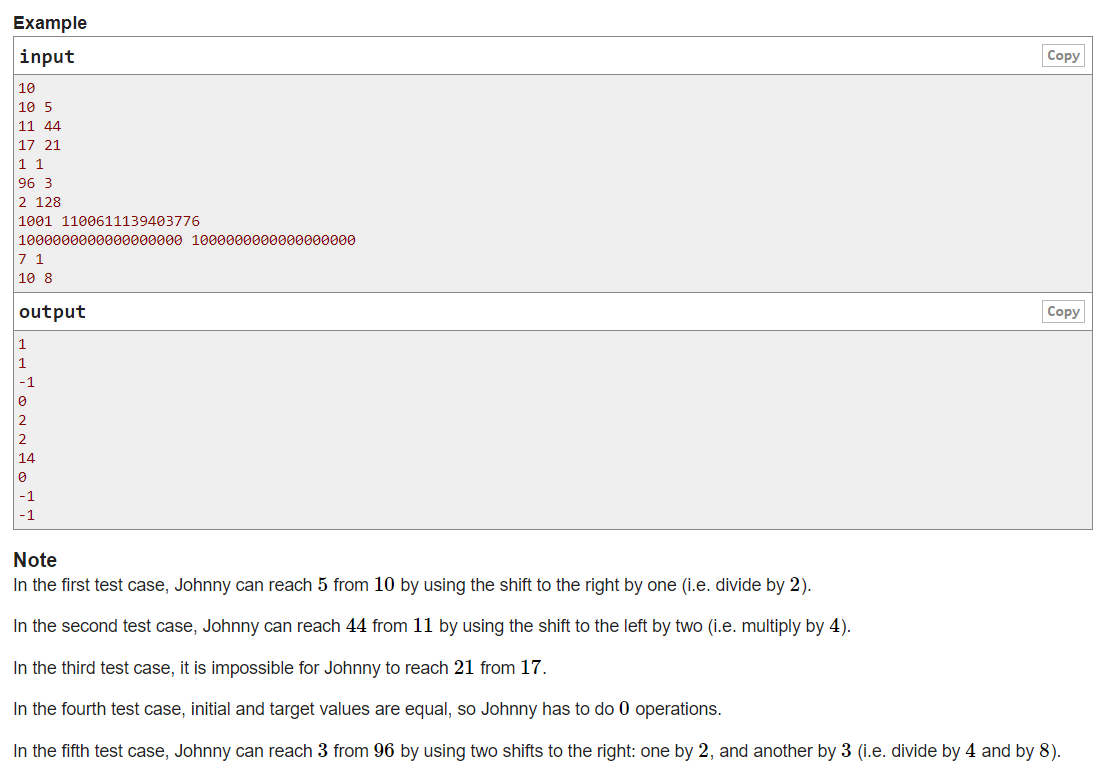
题意：给你两个数a和b，要求将a通过数次合法操作转换为b，输出最小的操作数，若无法转换为b，则输出-1。合法操作有：乘2、4、8，除以2、4、8。（除以操作只在能被整除的情况下执行）

思路：转换是双向的，所以我们认为问题是怎么由较大数转换为较小数。认为a是较大值，b是较小值，我们可以将问题转化为处理a / b的值。

b⋅t1​⋅t2​…tn​=a

t1​⋅t2​…tn​=a/b​

　　所以，如果特判a % b != 0必定无法转换，输出-1。然后令k =  a / b，用k去试探是否可以被2，4，8整除。由于需要输出最小操作数，所以能被较大数整除就除以较大数。遇到两种情况退出循环：

　　　　1、 k == 1，这时说明已经完成了操作，输出操作数即可。

　　　　2、 k != 1 && k % 2 == 1，这说明无法操作，输出-1。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1, M = 1;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lb lower_bound
#define ub upper_bound
#define endl '
'

int T, n;
bool vis[N];

int main()
{
    ios::sync_with_stdio(false);
    ull a, b;
    cin >> T;
    while (T--) {
        cin >> a >> b;
        if (a < b) swap(a, b);
        if (a % b) {
            cout << - 1 << endl;
            continue;
        }
        ll k = a / b;
        ll cnt = 0;
        while (k) {
            if (k % 8 == 0) {
                k /= 8;
                cnt++;
            }else if (k % 4 == 0) {
                k /= 4;
                cnt++;
            }else if (k % 2 == 0) {
                k /= 2;
                cnt++;
            }else if (k == 1) {
                break;
            }else {
                cnt = -1;
                break;
            }
        }
        cout << cnt << endl;
    }
    return 0;
}

总结：比赛时写了ios::sync_with_stdio(false);但是还是用了puts导致wa了两次，拖了些时间。下次注意不能再犯傻了。

 B. Johnny and His Hobbies

 

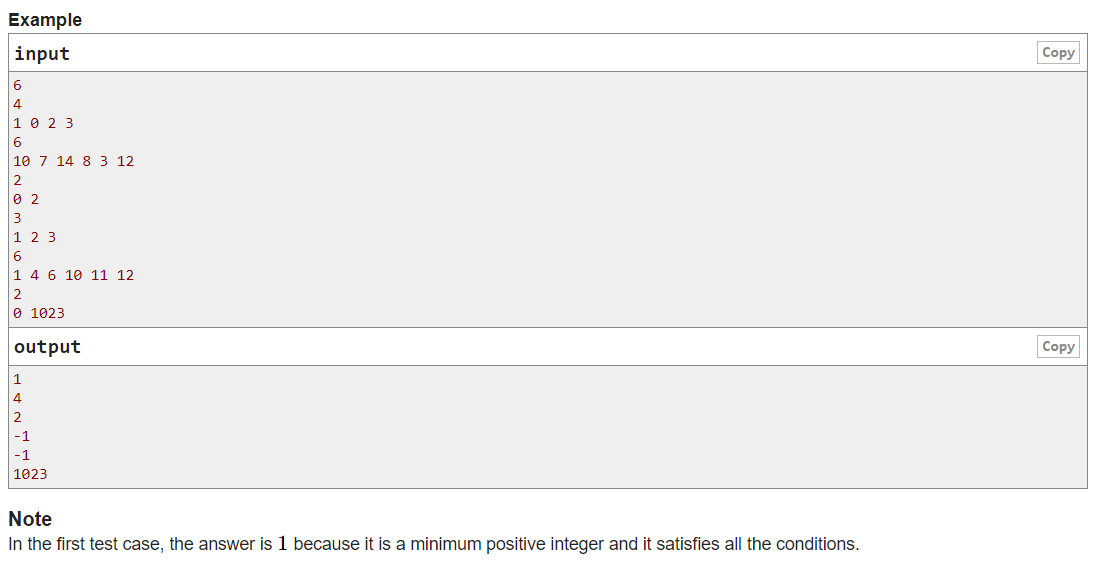
题意：给出一个集合，要求找到一个值k，使得集合中每一个值ai 变为 ai ^ k，仍使新集合等于原集合。

思路：因为所有n的总和不超过1024，所以我们可以从a[1] ^ a[2...n]枚举k的所有值。确定k值后在[2, n]里对每一个a[i]确定它对应的a[i] ^ k， 二分查找是否存在这个值。答案取最小值。时间复杂度大概是O(n2logn)。（应该没算错吧）

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 2048, M = 1;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lb lower_bound
#define ub upper_bound
#define endl '
'

int T, n;
ll a[N];
bool vis[N];

int bsearch(int l, int r, ll x)
{
    while (l < r) {
        int mid = l + r >> 1;
        if (a[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

int main()
{
    ios::sync_with_stdio(false);
    cin >> T;
    while (T--) {
        cin >> n;
        for (int i = 1; i <= n; i++) 
            cin >> a[i];
        if (n % 2) {
            cout << -1 << endl;
            continue;
        }
        int cnt = 0;
        ll res = 0x3f3f3f3f;
        sort(a+1, a+1+n);
        for (int i = 2; i <= n; i++) {
            ll ans = a[1] ^ a[i];
            cnt = 2;
            for (int j = 2; j <= n; j++) {
                if (j == i) continue;
                ll aim = ans ^ a[j];
                int pos = bsearch(1, n, aim);
                // cout << "j = " << j << "  pos = " << pos << endl;
                if (a[pos] == aim) {
                    cnt ++;
                }else {
                    break;
                }
            }
            if (cnt == n) {
                res = min(res, ans);
            }
        }
        if (res == 0x3f3f3f3f) res = -1;
        cout << res << endl;
    }
    return 0;
}

总结：拿到题目时就想过枚举k了，不过没敢写，硬是找规律找了好久。。。

C. Johnny and Another Rating Drop

 

题意：定义了一个不公平值，意味两个数的二进制表示中有多少位不相同。给出一个n，求出0, 1, ... , n中每两个连续的数的不公平值的和。

思路：比赛时我写了前几个值的和，找规律发现答案是2 * n - t，其中t为n和0的不公平值。

　　   以下为正解：容易发现第一位，逢1改变一次，所以第一位的总贡献为n；第二位，逢2改变一次，所以第二位总贡献为n/2；第三位，逢4改变一次，第三位总贡献则为n/4......

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1, M = 1;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lb lower_bound
#define ub upper_bound
#define endl '
'

ull T, n;
bool vis[N];

void solve1()            //暂未证明
{
    cin >> n;
    ll temp = n;
    ll cnt = 0;
    while (temp) {
        if (temp & 1) cnt++;
        temp >>= 1;
    }
    cout << 2ll * n - cnt << endl;
}

void solve2()
{
    cin >> n;
    ll temp = n;
    ll ans = 0;
    ll now = 1;
    while (temp) {
        ans += n / now;
        now *= 2;
        temp >>= 1;
    }
    cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin >> T;
    while (T--) {
        // solve1();

        solve2();
    }
    return 0;
}

D. Johnny and Contribution 

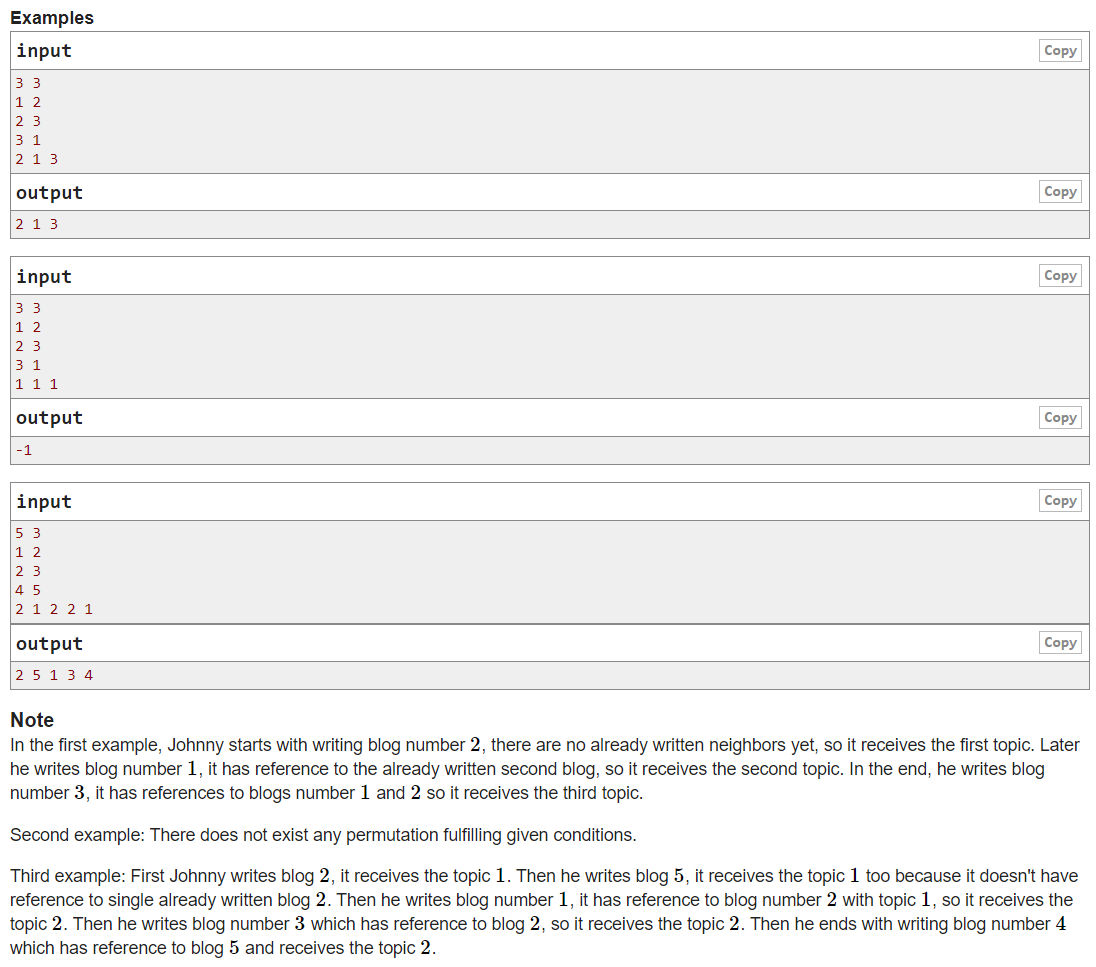
题意：有n个点，m条边的无向图。每一个点有一个期望值，每次给点赋值的时候，必须赋值为所有与它直接连接的点中的mex值（即未出现过的最小自然数），求一个赋值顺序使得每个点的值是它的期望值。

思路：模拟，从期望点权最小的点开始赋值。维护一个mx数组，使得mx数组里的值是当前点所连的点里的最大值。（其实就是暴力）

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5, M = 1;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lb lower_bound
#define ub upper_bound
#define endl '
'

int T, n, m;
bool vis[N];
struct node{
    int id, val;
}a[N];
vector<int> v[N];
int mx[N], ans[N];

bool cmp(node a, node b)
{
    if (a.val == b.val) {
        return a.id < b.id;
    }else{
        return a.val < b.val;
    }
}

int main()
{
    //ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int l, r;
        Sca(l); Sca(r);
        v[l].pb(r); v[r].pb(l);
    }
    for (int i = 1; i <= n; i++) {
        int val;
        Sca(a[i].val);
        a[i].id = i;
    }
    sort(a+1, a+1+n, cmp);
    for (int i = 1; i <= n; i++) {
        int x = a[i].id, val = a[i].val;
        if (mx[x] != val - 1) {
            puts("-1");
            return 0;
        }
        ans[i] = x;
        for (auto i : v[x]) {
            if (mx[i] == val - 1) {
                mx[i] = val;
            }
        }
    }
    for (int i = 1; i <= n; i++) printf("%d ", ans[i]);
    return 0;
}

总结：比赛时看了半天硬是没有看懂题意，英语果然还是很重要。

E. Johnny and Grandmaster

 

题意：给出一个序列k，要求将k分为两个集合，求得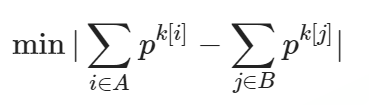

思路：有一个前置知识：

　　   所以我们就可以根据贪心策略，先将k降序排序。定义ans为最终答案，每当ans = 0时，让ans加上p的k[i]次；ans != 0时，ans减去p的k[i]次。

　　   这样大值被消化了，最后得到的即为最小值。

　　   值得注意的是，过程中处处用到对1e9+7取余，所以ans = 0时并不一定真的是ans = 0，而是ans是1e9+7的倍数。所以我们每次多运算一个值，让它对其他数取余，这样当两个值都等于0时，就是ans真正为0。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+5, M = 1, MOD = 1e9+7, _MOD = 1e9+5;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lb lower_bound
#define ub upper_bound
#define endl '
'

int T, n, p, k[N];
bool vis[N];
bool cmp(int a, int b)
{return a > b;}

ll QuickPow(ll a, ll b, ll mod)
{
    ll ans = 1;
    while (b) {
        if (b & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return ans % mod;
}

void solve()
{
    scanf("%d%d", &n, &p);
    for (int i = 1; i <= n; i++) Sca(k[i]);
    if (p == 1) {
        cout << n % 2 << endl;
        return;
    }
    sort(k + 1, k + 1 + n, cmp);
    ll res = 0, ans = 0;
    for (int i = 1; i <= n; i++) {
        if (!ans && !res) {
            ans += QuickPow(p, k[i], MOD);
            res += QuickPow(p, k[i], _MOD);
        }else{
            ans = ((ans - QuickPow(p, k[i], MOD)) + MOD) % MOD;
            res = ((res - QuickPow(p, k[i], _MOD)) + _MOD) % _MOD;
        }
    }
    cout << ans << endl;
}

int main()
{
    // ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

F. Johnny and Megan's Necklace