https://blog.csdn.net/qq_37941471/article/details/80710099 八大排序算法
https://blog.csdn.net/qq_37623612/article/details/80312121 直接插入排序
其余排序:https://www.jianshu.com/p/502153724b91
------------------------------------【整理】-----------------------------
复杂度总结:
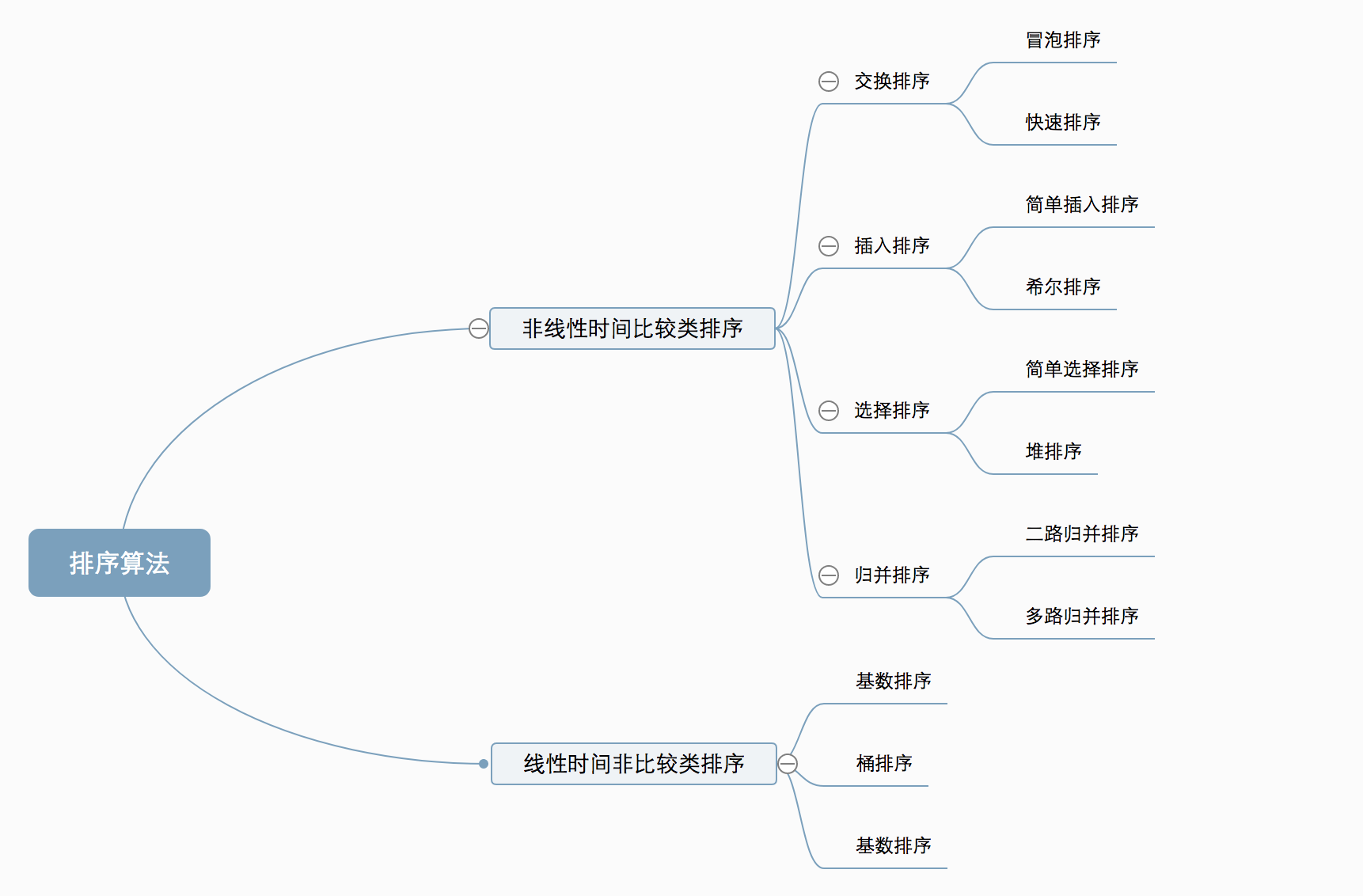
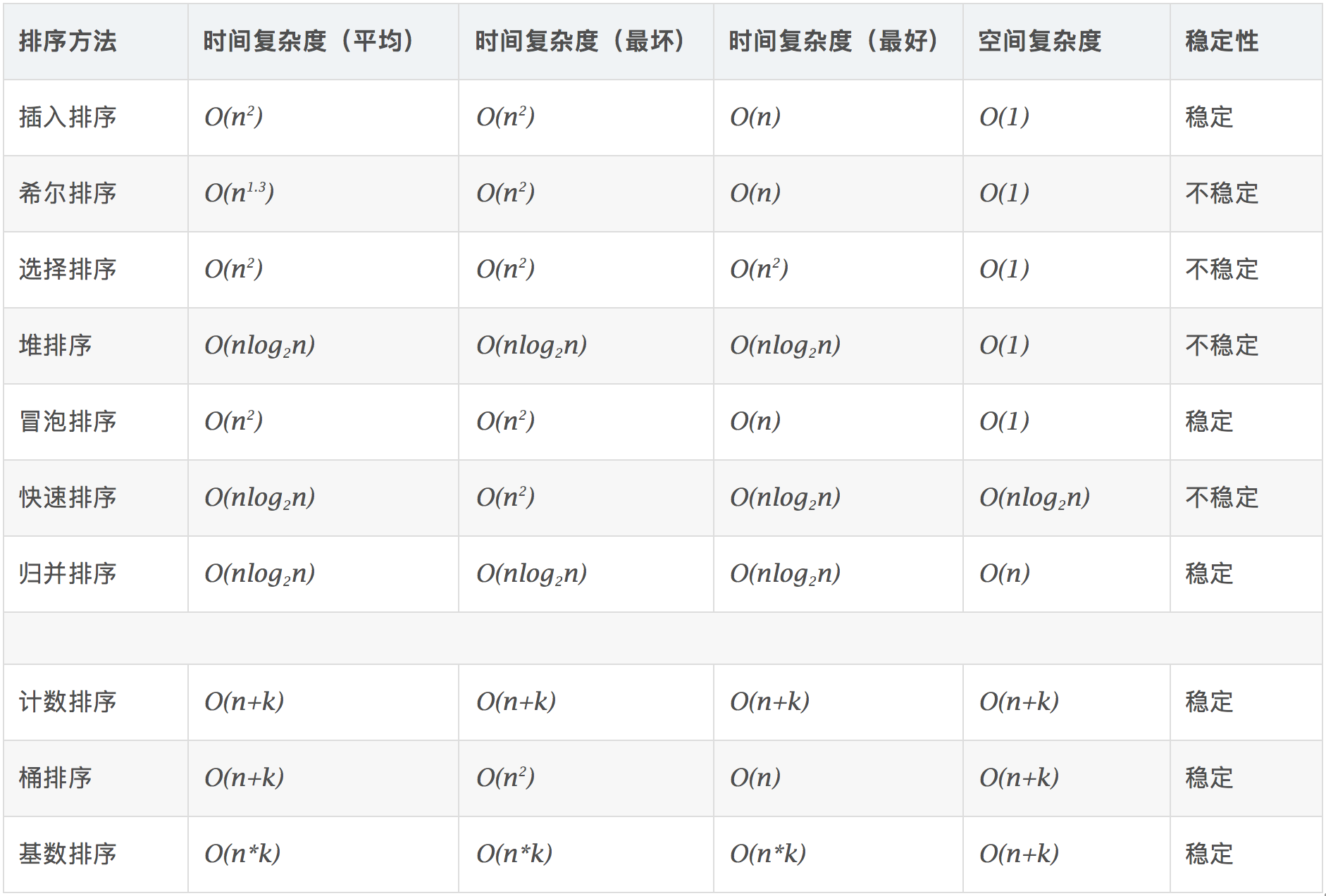
插入排序
1.直接插入排序
//构建有序序列, 已排序序列中,从后向前扫描,插入到有序序列中。
//复杂度上来说,排序比较次数+移动次数,最好是n,最坏是n^2,平均是n^2
void InsertSort(int *array, int n)
{
int i, j;
int temp;
for (int i = 1; i < n; i++)
{
j = i;
temp = array[i];//预要插入的数字,记录
while (j > 0 && array[j - 1] > temp)
{
array[j] = array[j - 1]; //从后向前扫描有序序列,大于就向后移位,空出位置给temp插入
j--;
}
array[j] = temp;
}
}
2.折半插入排序
//折半插入排序
//在有序区上找空闲,用的是二分查找方法
//nlogn
void binInsertSort(int* array, int n)
{
int i, j,low,high,mid;
int temp;
for (int i = 1; i < n; i++)
{
if (array[i] < array[i - 1])
{
temp = array[i];
low = 0;
high = i - 1;
while (low <= high)
{
mid = (low + high) / 2;
if (temp < array[mid])
high = mid - 1;
else
low = mid + 1;
}
for (j = i - 1; j >= high + 1; j--)//集中元素后移
{
array[j + 1] = array[j];
}
array[high + 1] = temp; //插入元素
}
}
}
3. 希尔排序
//设置增量d,减少增量,对每一组增量间隔的数进行直接插入排序
//复杂度是
void ShellSort(int* array, int n)
{
int i, j, d;
int temp;
d = n / 2; //设置增量
while (d > 0)
{
for (i = d; i < n; i++)//对所有组采用插入排序
{
temp = array[i];//对相隔d个为止的一组采用直接插入排序
j = i - d;
while (j >= 0 && temp < array[i])
{
array[j + d] = array[j];
j = j - d;
}
array[j + d] = temp;
}
d = d / 2;
}
}
交换排序系列
1.选择排序
从每一趟待排元素中,选取关键字最小的元素,放在已排序的最后,适合从大量元素中,选择一部分排序元素
#include <algorithm>
using namespace std;
void SelectSort(int* array, int n)
{
int i, j, k;//k 定位
for (i = 0; i < n - 1; i++)
{
k = i;
for (j = i + 1; j < n; j++)
{
if (array[j] < array[k])
{
k = j;
}
}
if (k != j)
{
swap(array[i], array[k]);
}
}
}
2.冒泡排序
没什么好说的,交换次序,进行n轮,浮动到最前。
#include <algorithm>
using namespace std;
void BubbleSort(int* array, int n)
{
int i, j;
for (i = 0; i < n - 1; i++)
{
for (j = n - 1; j > i; j--)
{
if (array[j] < array[j - 1])
{
swap(array[j], array[j - 1]);
}
}
}
}
3.快速排序
为什么快排是不稳定的:
举个例子
待排数组 6 9 9 10 11
我们选择第一个9作为主元(过程是随机的),若把小于等于放在主元的左边,则第二个9就跑到第一个9左面了,从而导致不稳定
主元的选择是随机的,导致不稳定的原因在于我们无法保证每次都是稳定的,所以它是不稳定的。
冒泡排序改进而来
一趟划分,找一个中心点,然后把小于他的放在左边,大于他的放在右边。
递归左右。
int partition(int array[], int s, int t) //一趟划分
{
int i = s, j = t;
int temp = array[i];//第一个为基准,然后记录这个。
while (i < j)//俩端交替向中扫描,直到i=j;
{
while (j > i&& array[j] >= temp) //从右向左扫描,找到一个小于temp的,交换到位置i上
{
j--;
}
array[i] = array[j]; //右边扫描结束
while (i < j && array[i] <= temp) //找到第一个大于temp的,交换到位置j上
{
i++;
}
array[j] = array[i]; //左边扫描结束
}
array[i] = temp; //中心点放上位置。
}
void QuickSort(int* array, int s, int t)
{
int i;
if (s < t) //区间内至少俩个元素
{
i = partition(array, s, t);
QuickSort(array, s, i - 1); //递归
QuickSort(array, i + 1, t);
}
}
堆排序
#include <iostream>
using namespace std;
int heap[100] = { 0,4,3,1,5,6 };
int n = 5;
void swap(int& a,int& b) {
int temp = a;
a = b;
b = temp;
};
//向下建堆
void downHeap(int low, int high)
{
int i = low, j = i * 2;
while (j <= high)
{
if (j + 1 <= high && heap[j+1] < heap[j])
j = j + 1; //子节点中小的那个
if (heap[j] < heap[i])
{
swap(heap[j], heap[i]);//交换
i = j;
j = i * 2;
}
else
{
break;
}
}
}
//建小根堆操作
void creatHeap(const int n)
{
for (int i = n / 2; i >= 1; i--)
{
downHeap(i, n);
}
}
//删除堆顶元素
void deleteHeap(int& n)
{
heap[1] = heap[n--];
downHeap(1, n);
}
//插入堆顶元素(要向上调整,一次调整)
void upHeap(int low, int high)
{
int i = high, j = i / 2;
while (j >= low)
{
if (heap[j] > heap[i])
{
swap(heap[i], heap[j]);
i = j;
j = i / 2;
}
else
{
break;
}
}
}
//增加
void insertHeap(int& n,int value)
{
heap[++n] = value;
upHeap(1, n);
}
//堆排序(小顶堆会排序为逆序)
void HeapSort( int n)
{
for (int i = n; i > 1; i--)
{
swap(heap[i], heap[1]);
downHeap(1, i - 1);
}
}
int main()
{
creatHeap(n);
//HeapSort(n);
insertHeap(n, 2);
HeapSort(n);
for (int i = 1; i <n; i++)
{
cout << heap[i] << " ";
}
cout << heap[n] << endl;
}
基数排序
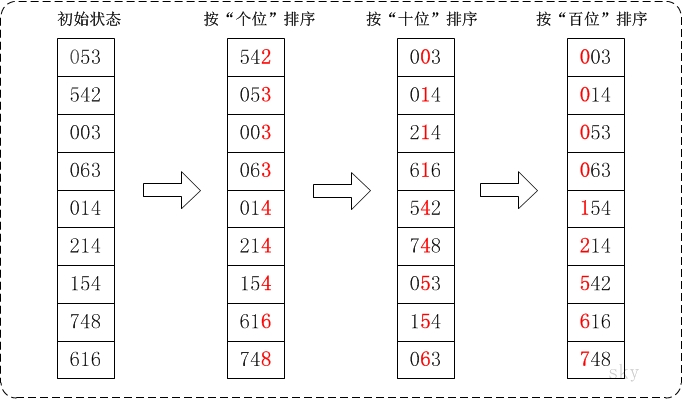
时间复杂度:每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d2n) ,当然d要远远小于n,因此基本上还是线性级别的。系数2可以省略,且无论数组是否有序,都需要从个位排到最大位数,所以时间复杂度始终为O(dn) 。其中,n是数组长度,d是最大位数。
空间复杂度: 基数排序的空间复杂度为O(n+k),其中k为桶的数量,需要分配n个数。