两个栈实现队列 两个队列实现栈

转自两个栈实现队列 两个队列实现栈

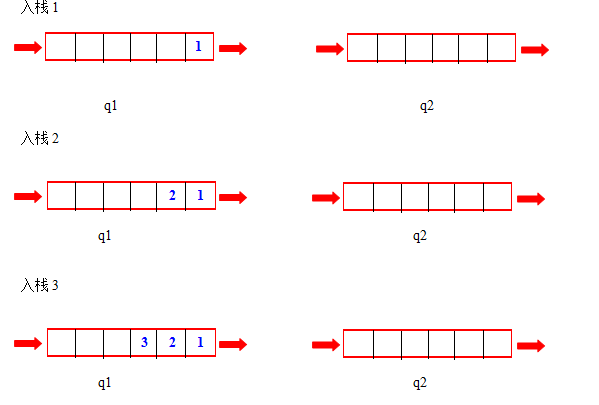
为说明思想，假设队列、栈都很大，不会出现满的情况。

1. 两个栈实现队列

//前提已知：
struct Stack
{
    int top;   　　//栈顶指针
    int stacksize;//栈的大小
    int *s;    　　//栈底指针
};
void InitStack(Stack *s)；
void Push(Stack *s, int k);
int Pop(*s);
int IsStackEmpty(*s);
int IsStackFull(*s);

实现一

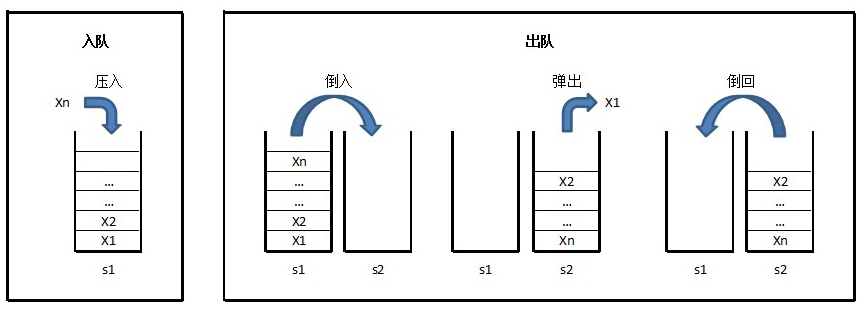
思路:s1是入栈的，s2是出栈的。

• 入队列，直接压到s1是就行了
• 出队列，先把s1中的元素全部出栈压入到s2中，弹出s2中的栈顶元素；再把s2的所有元素全部压回s1中

实现二

思路：s1是入栈的，s2是出栈的。保证所有元素都在一个栈里面

• 入队列时：如果s1为空，把s2中所有的元素倒出压到s1中；否则直接压入s1
• 出队列时：如果s2不为空，把s2中的栈顶元素直接弹出；否则，把s1的所有元素全部弹出压入s2中，再弹出s2的栈顶元素

比较：与实现一相比较，出队列时不必每次都捣鼓了。

实现三

思路：s1是入栈的，s2是出栈的。

• 入队列：直接压入s1即可
• 出队列：如果s2不为空，把s2中的栈顶元素直接弹出；否则，把s1的所有元素全部弹出压入s2中，再弹出s2的栈顶元素

比较：与实现二相比较，入队直接入即可，感觉此时已是最优。

参考代码

void EnQueue(Stack *s1, Stack *s2, int k)
{
    Push(s1, k);
}

int DeQueue(Stack *s1, Stack*s2)
{
    if(IsStackEmpty(s2) == 1)
    {
        while(IsStackEmpty(s1) == 0)
            {
                Push(s2, Pop(s1));
            }
    }
    if(IsStackEmpty(s2) == 1)
    {
        printf("Empty!
");
    }
    return Pop(s2);    

 

2. 两个队列实现栈

//前提已知
typedef struct queue
{
        int queuesize;
        int head, tail;
        int *q;
}Queue;

void InitQueue(Queue *q);
void EnQueue(Queue *q, int key);
int DeQueue(Queue *q);
int SizeOfQueue(Queue *q);
int IsQueueEmpty(Queue *q);
int IsQueueFull(Queue *q);

实现一

思路

    q1是专职进出栈的，q2只是个中转站

• 入栈：直接入队列q1即可
• 出栈：把q1的除最后一个元素外全部转移到队q2中,然后把刚才剩下q1中的那个元素出队列。之后把q2中的全部元素转移回q1中

图示

   

参考代码

void Push(Queue *q1, Queue *q2, int k)
{
        EnQueue(q1, k);
}

int  Pop(Queue *q1, Queue *q2)
{
    int tmp;
    if(IsQueueEmpty(q1) == 1)
    {
       printf("Stack Empty!
");
    }
    else
    {
        while(SizeOfQueue(q1) != 1)
        {
            EnQueue(q2, DeQueue(q1));
        }
        tmp = DeQueue(q1);
        while(IsQueueEmpty(q2) == 0)
        {
            EnQueue(q1, DeQueue(q2));
        }
        return tmp;
    }
} 

实现二

思路

q1是专职进出栈的，q2只是个中转站。元素集中存放在一个栈中，但不是指定。

定义两个指针：pushtmp:所指专门进栈的队列； tmp：指向临时作为中转站的另一个栈。

• 入栈：直接入pushtmp所指队列即可
• 出栈：把pushtmp的除最后一个元素外全部转移到队列tmp中,然后把刚才剩下q1中的那个元素出队列

比较

实现二，转移到另外一个队列后不用返回了，这样减少了转移的次数。

参考代码

void Push(Queue *q1, Queue *q2, int k)
{
        Queue *pushtmp, *tmp;
        if(IsQueueEmpty(q1) == 0)
        {
            pushtmp = q1;
            tmp = q2;
        }
        else
        {
            pushtmp = q2;
            tmp = q1;
        }
        EnQueue(pushtmp, k);
}

int  Pop(Queue *q1, Queue *q2)
{
    int tmpvalue;
    Queue *pushtmp, *tmp;
    if(!IsQueueEmpty(q1))
    {
        pushtmp = q1;
        tmp = q2;
    }
    else
    {
        pushtmp = q2;
        tmp = q1;
    }

    if(IsQueueEmpty(pushtmp))
    {
       printf("Stack Empty!
");
    }
    else
    {
        while(SizeOfQueue(pushtmp) != 1)
        {
            EnQueue(tmp, DeQueue(pushtmp));
        }
        tmpvalue = DeQueue(pushtmp);
        return tmpvalue;
    }
}