定义
对于有向无权无环图,进行拓扑排序
实现方式
- Kahn算法
- 基于DFS的拓扑排序算法
Kahn算法
优化前时间复杂度O((n^{2}))
排序的过程
1.对于DAG,先输出没有前驱的点
2.把与前驱相关的边删除
3.继续输出没有前驱的点
4.重复前者,直到DAG为空或者没有前驱
如果我们有如下的一个有向无环图,我们需要对这个图的顶点进行拓扑排序,过程如下:
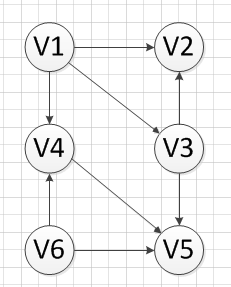
首先,我们发现V6和v1是没有前驱的,所以我们就随机选去一个输出,我们先输出V6,删除和V6有关的边,得到如下图结果:
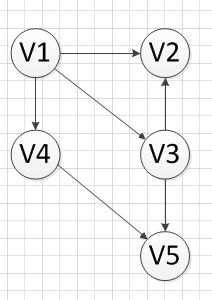
然后,我们继续寻找没有前驱的顶点,发现V1没有前驱,所以输出V1,删除和V1有关的边,得到下图的结果:
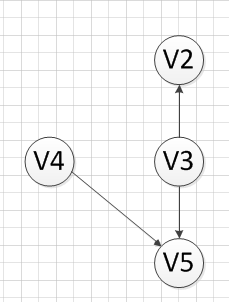
然后,我们又发现V4和V3都是没有前驱的,那么我们就随机选取一个顶点输出(具体看你实现的算法和图存储结构),我们输出V4,得到如下图结果:
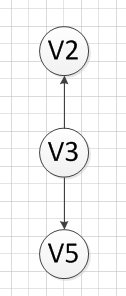
然后,我们输出没有前驱的顶点V3,得到如下结果:
然后,我们分别输出V5和V2,最后全部顶点输出完成,该图的一个拓扑序列为:
v6–>v1—->v4—>v3—>v5—>v2
应用
给出n个点,m个关系
再给出u,v,表示u比v厉害
然后进行排序
邻接矩阵版Kahn算法的拓扑排序
复杂度O((n^{2}))
传送门
裸拓扑排序
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int N=510;
std::vector<int> v;
int g[N][N];
int degree[N];
int n;
void init(){
memset(g,0,sizeof(g));
v.clear();
memset(degree,0,sizeof(degree));
}
void topological_sort(){
for(int i=1;i<=n;i++){
int k;//假设无环
for(int j=1;j<=n;j++){
if(degree[j]==0){//找到一个入度为0的点
degree[j]--;//标记为-1,防止下一次循环的时候还会访问到这个点
k=j;
v.push_back(j);
break;
}
}
for(int j=1;j<=n;j++){//从点k出发到达的点都给取消掉,把j的入度减1
if(g[k][j]==1)degree[j]--;
}
}
}
void print(){
printf("%d",v[0]);
for(int i=1;i<v.size();i++){
printf(" %d",v[i]);
}
putchar('
');
}
int main(){
int m;
while(~scanf("%d%d",&n,&m)){
init();
while(m--){
int u,v;
scanf("%d%d",&u,&v);
if(g[u][v]==0){//去重边,防止入度混乱
g[u][v]=1;
degree[v]++;
}
}
topological_sort();
print();
}
return 0;
}
vector版Kahn算法拓扑排序
vector+队列优化
时间复杂度O((n^{2}))
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>
using namespace std;
const int N=505;
std::vector<int> g[N];
std::vector<int> v;
int degree[N];
int n;
void init(){
memset(degree,0,sizeof(degree));
v.clear();
for(int i=0;i<=n;i++){
g[i].clear();
}
}
void kahn(){
int k=0;
queue<int>q;
for(int i=1;i<=n;i++){//自己撸的算法里直接把邻接的那几个结点拿来用了
if(!degree[i])q.push(i);
}
while(!q.empty()){
int k=q.front();q.pop();
v.push_back(k);
for(int j=0;j<g[k].size();j++){//消除从k出发,到达的点的边
int x=g[k][j];
degree[x]--;
if(!degree[x])q.push(x);//如果边消去后该点是无入度的,加入队列
}
}
}
void print(){
printf("%d",v[0]);
for(int i=1;i<v.size();i++){
printf(" %d",v[i]);
}
putchar('
');
}
int main(){
int m;
while(~scanf("%d%d",&n,&m)){
init();
while(m--){
int u,v;
scanf("%d%d",&u,&v);
g[u].push_back(v);
degree[v]++;
}
kahn();
if(v.size()!=n){
printf("有环
");
}else{
print();
}
}
return 0;
}
结构体
优先队列优化---序列约束
假如要求序列小的先输出,前面的邻接矩阵版kahn算法也可以实现
复杂度为O(V+E)
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <queue>
using namespace std;
const int N=505;
std::vector<int> g[N];
std::vector<int> v;
int degree[N];
int n;
void init(){
memset(degree,0,sizeof(degree));
v.clear();
for(int i=0;i<=n;i++){
g[i].clear();
}
}
void kahn(){
int k=0;
priority_queue<int,vector<int>,greater<int> >q;//表示从小到大,dijkstra算法那里存入的是结构体,而且在结构体里重载运算符了,所以不需要加这些,优先队列默认从大到小,输出第一个是top()
for(int i=1;i<=n;i++){//自己撸的算法里直接把邻接的那几个结点拿来用了
if(!degree[i])q.push(i);
}
while(!q.empty()){
int k=q.top();q.pop();
v.push_back(k);
for(int j=0;j<g[k].size();j++){//消除从k出发,到达的点的边
int x=g[k][j];
degree[x]--;
if(!degree[x])q.push(x);//如果边消去后该点是无入度的,加入队列
}
}
}
void print(){
printf("%d",v[0]);
for(int i=1;i<v.size();i++){
printf(" %d",v[i]);
}
putchar('
');
}
int main(){
int m;
while(~scanf("%d%d",&n,&m)){
init();
while(m--){
int u,v;
scanf("%d%d",&u,&v);
g[u].push_back(v);
degree[v]++;
}
kahn();
if(v.size()!=n){
printf("有环
");
}else{
print();
}
}
return 0;
}
基于dfs的拓扑排序
半成品
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
const int N=505;
int n,m;
std::vector<int> v;
void init(){
memset();
v.clear();
}
void print(){
printf("%d",v[0]);
for(int i=1;i<v.size();i++){
printf(" %d",v[i]);
}
putchar('
');
}
void dfs(){
}
int main(){
while(~scanf("%d%d",&n,&m)){
init();
while(m--){
int u,v;
scanf("%d%d",&u,&v);
}
dfs();
print();
}
return 0;
}