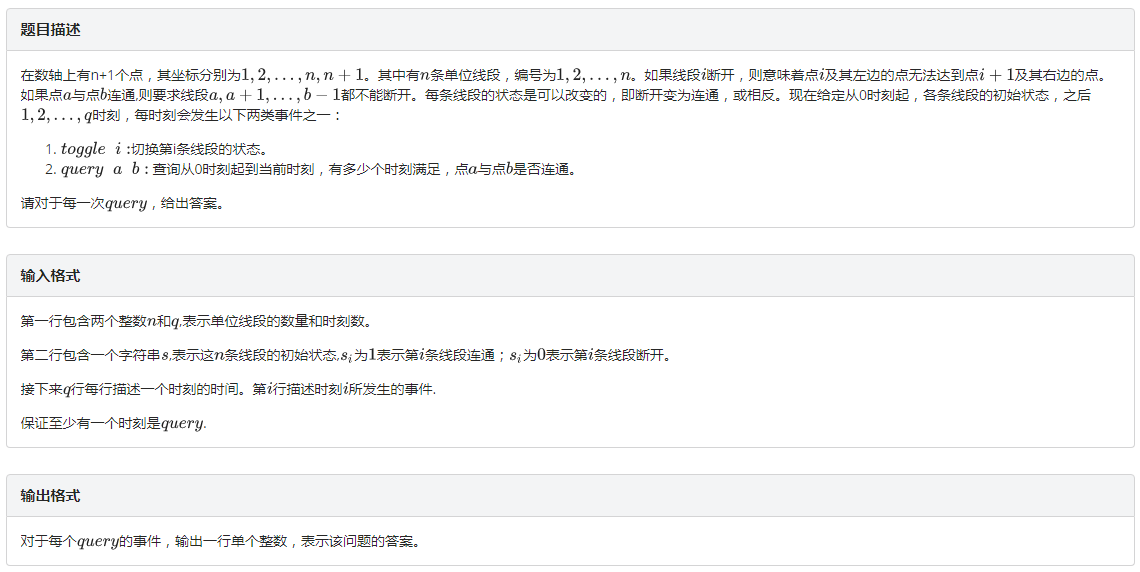
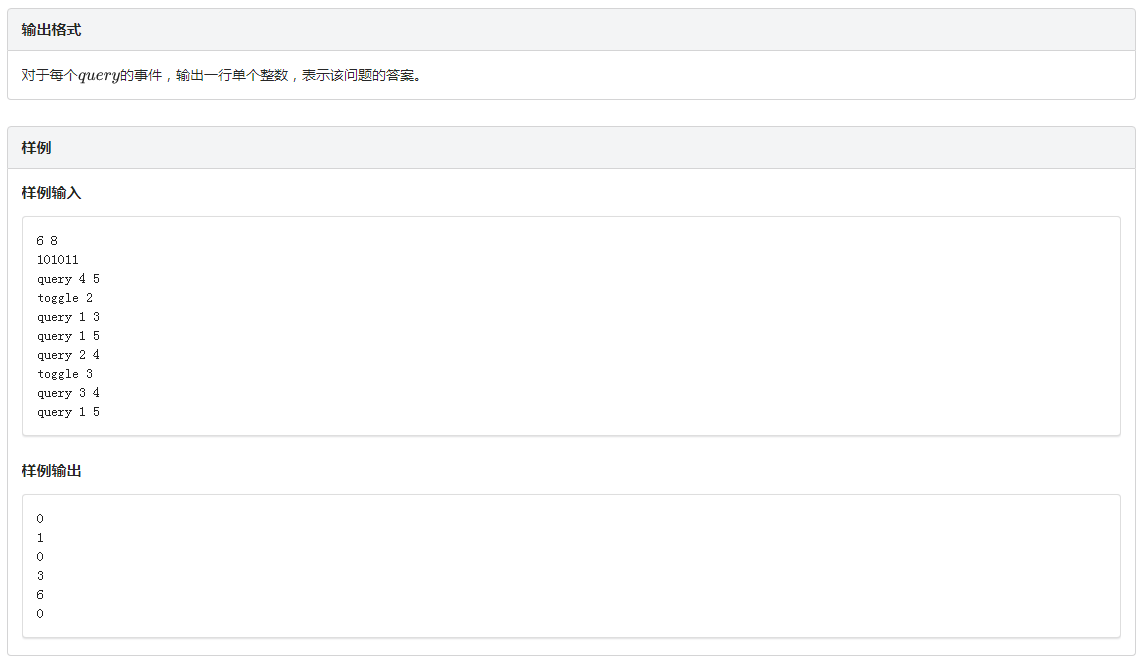
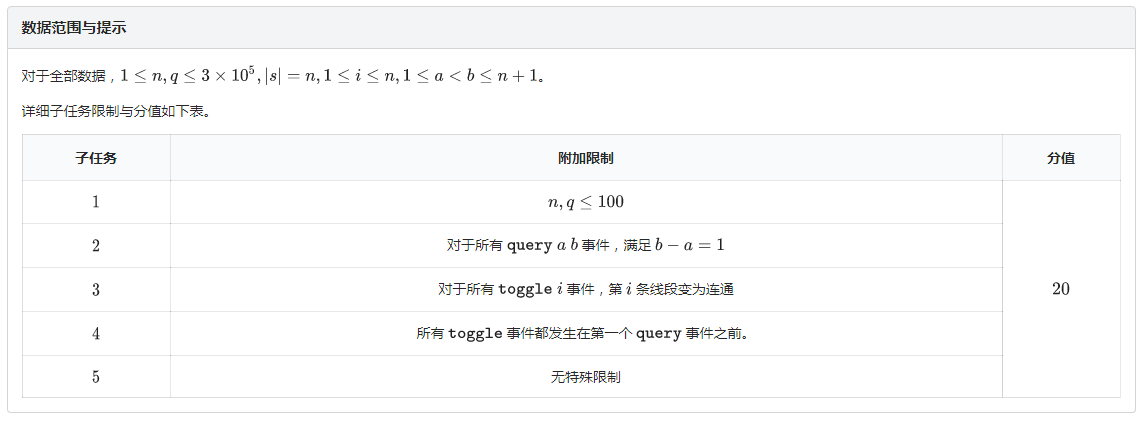
题目:
分析:
良心出题人给超多部分分(错乱
又是喜闻乐见的把线段((x,y))放到平面坐标系的点((x,y))上,我们尝试得到这个点上的值
我们改变一个单位线段(x)的状态,考虑它的影响范围,在线树状数组之类的数据结构维护连续(1)的线段,可以得出一个下标(x)的影响范围((l,r))
改变这个点会影响左上角((l,x)),右下角((x,r))的矩形
一对点假设在(t_1)时刻连通,(t_2)时刻断开,那么会产生(t_2-t_1)的贡献
每次在(t)时刻连通时,我们将矩形减(t)
每次在(t)时刻断开时,我们将矩形加(t)
查询某个点值为(v)时,如果当前(t)时刻状态为连通,答案为(t+v),否则为(v)
使用差分变成单点修改矩形查询
二维数据结构卡空间?CDQ分治一下吧
也当复习CDQ分治了
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<vector>
#define maxn 2000005
#define MOD 998244353
using namespace std;
inline long long getint()
{
long long num=0,flag=1;char c;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9')num=num*10+c-48,c=getchar();
return num*flag;
}
int n,q,qcnt,cnt;
char s[maxn];
struct node{
int op,x,y,t,val,id,ans;
}Q[maxn],tmp[maxn];
int A[maxn];
struct BT{
int N;
int t[maxn];
inline void update(int x,int num)
{for(int i=x;i<=N;i+=i&(-i))t[i]+=num;}
inline int getans(int x)
{int num=0;for(int i=x;i;i-=i&(-i))num+=t[i];return num;}
}B,T;
int ans[maxn];
inline bool cmp2(node x,node y)
{return x.y!=y.y?x.y<y.y:x.t<y.t;}
inline bool cmp1(node x,node y)
{return x.x!=y.x?x.x<y.x:cmp2(x,y);}
inline bool check(int x,int y)
{return B.getans(y)-B.getans(x-1)>y-x;}
inline int getl(int x)
{
int l=1,r=x;
while(l<r){int mid=(l+r)>>1;if(check(mid,x))r=mid;else l=mid+1;}
return l;
}
inline int getr(int x)
{
int l=x,r=n;
while(l<r){int mid=(l+r+1)>>1;if(check(x,mid))l=mid;else r=mid-1;}
return r;
}
inline void solve(int l,int r)
{
if(l==r)return;
int mid=(l+r)>>1;
solve(l,mid),solve(mid+1,r);
int pre=l-1;
for(int i=mid+1;i<=r;i++)
{
while(pre<mid&&Q[pre+1].y<=Q[i].y)
{
pre++;
if(Q[pre].op==2)T.update(Q[pre].t,Q[pre].val);
}
if(Q[i].op==1)Q[i].ans+=T.getans(Q[i].t);
}
for(int i=l;i<=pre;i++)if(Q[i].op==2)T.update(Q[i].t,-Q[i].val);
int pl=l,pr=mid+1,num=l-1;
while(pl<=mid&&pr<=r)
{
if(cmp2(Q[pl],Q[pr]))tmp[++num]=Q[pl++];
else tmp[++num]=Q[pr++];
}
while(pl<=mid)tmp[++num]=Q[pl++];
while(pr<=r)tmp[++num]=Q[pr++];
for(int i=l;i<=r;i++)Q[i]=tmp[i];
}
int main()
{
B.N=n=getint(),T.N=q=getint();
scanf("%s",s+1);
for(int i=1;i<=n;i++)A[i]=(s[i]=='1'),B.update(i,A[i]);
for(int i=1;i<=q;i++)
{
scanf("%s",s);
if(s[0]=='q')
{
int x=getint(),y=getint()-1;
if(check(x,y))Q[++cnt]=(node){1,x,y,i,i,++qcnt,0};
else Q[++cnt]=(node){1,x,y,i,0,++qcnt,0};
}
else
{
int x=getint(),l=getl(x-1),r=getr(x+1);
if(l==x-1&&!A[l])l++;if(r==x+1&&!A[r])r--;
if(A[x])
{
Q[++cnt]=(node){2,l,x,i,i,0,0};
Q[++cnt]=(node){2,x+1,r+1,i,i,0,0};
Q[++cnt]=(node){2,x+1,x,i,-i,0,0};
Q[++cnt]=(node){2,l,r+1,i,-i,0,0};
}
else
{
Q[++cnt]=(node){2,l,x,i,-i,0,0};
Q[++cnt]=(node){2,x+1,r+1,i,-i,0,0};
Q[++cnt]=(node){2,x+1,x,i,i,0,0};
Q[++cnt]=(node){2,l,r+1,i,i,0,0};
}
A[x]^=1,B.update(x,A[x]?1:-1);
}
}
sort(Q+1,Q+cnt+1,cmp1);
solve(1,cnt);
for(int i=1;i<=cnt;i++)if(Q[i].op==1)ans[Q[i].id]+=Q[i].ans+Q[i].val;
for(int i=1;i<=qcnt;i++)printf("%d
",ans[i]);
}
