题解
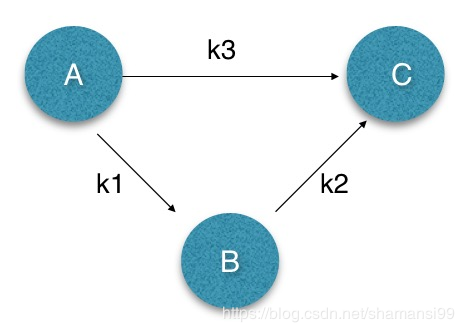
令x-y<=z表示x最大比y大z。
若b-a<=k1, c-b<=k2, c-a<=k3,那么c-a最大为多少呢?显然应该等于min(k1+k2, k3)。可以用下图来表示示(不擅图丑勿怪)
C++堆优化代码
//链式前向星存图+迪杰斯特拉堆优化 #include<iostream> #include<cstdio> #include<queue> #include<cstring> using namespace std; const int MAX=100005; const int MAXN=400009; const int INF=0x3f3f3f3f; int head[MAX],cnt=0; int t,n,a,b,len; int dist[MAX]; bool vis[MAX]; struct Edge{ //链式前向星 int next,val,to; }Edge[MAXN]; inline void add(int u,int v,int w) { Edge[cnt].to=v; Edge[cnt].val=w; Edge[cnt].next=head[u]; head[u]=cnt++; } struct node { int pos,dist; //点的位置及距离 node(){} node(int p,int d) { pos=p; dist=d; } bool operator < (const node &rhs)const //重载 < { return dist>rhs.dist; } }; void Dij(int start) { priority_queue<node>que; for(int i=1;i<=t;i++) { dist[i]=INF; vis[i]=false; } dist[start]=0; que.push(node(start,0)); while(!que.empty()) { node temp=que.top(); //优先队列为首的元素及dist数组的最小值 que.pop(); int v=temp.pos; //筛选出最小值 if(vis[v])continue; //判断是否已经找到最小值 ,是的话跳过 vis[v]=true; for(int i=head[v];i!=-1;i=Edge[i].next) //用最小值的点为弧尾的边更新距离 { int to=Edge[i].to; if(dist[to]>dist[v]+Edge[i].val) { dist[to]=dist[v]+Edge[i].val; que.push(node(to,dist[to])); } } } } int main() { while(scanf("%d%d",&t,&n)!=EOF) { memset(head,-1,sizeof(head)); for(int i=0;i<n;i++) { scanf("%d%d%d",&a,&b,&len); add(a,b,len); //add(b,a,len); } Dij(1); printf("%d ",dist[t]); } return 0; }
C++配对堆优化
#include <bits/stdc++.h> #include<ext/pb_ds/priority_queue.hpp> using namespace std; using namespace __gnu_pbds; typedef pair<int,int> pii; typedef __gnu_pbds::priority_queue<pii,greater<pii>,pairing_heap_tag> Heap; const int maxn=1e5+10; const int INF=0x3f3f3f3f; int n,m,s; struct Edge{ int u,v,w; Edge(int _u=0,int _v=0,int _w=0){u=_u,v=_v,w=_w;} }; vector<Edge> E; vector<int> G[maxn]; void addedge(int u,int v,int w) { E.push_back(Edge(u,v,w)); G[u].push_back(E.size()-1); } int d[maxn]; void dijkstra() { memset(d,0x3f,sizeof(d)); Heap Q; Heap::point_iterator id[maxn]; d[s]=0; id[s]=Q.push(make_pair(d[s],s)); while(!Q.empty()) { int u=Q.top().second; Q.pop(); for(int i=0;i<G[u].size();i++) { Edge &e=E[G[u][i]]; int v=e.v; if(d[v]>d[u]+e.w) { d[v]=d[u]+e.w; if(id[v]!=0) Q.modify(id[v],make_pair(d[v],v)); else id[v]=Q.push(make_pair(d[v],v)); } } } } int main() { while(~scanf("%d%d",&n,&m)){ s = 1;//起点 //memset(d,0,sizeof d); memset(G,0,sizeof G); for(int i=1;i<=m;i++) { int u,v,w; scanf("%d%d%d",&u,&v,&w); addedge(u,v,w); } dijkstra(); //for(int i=1;i<=n;i++) printf("%d%s",d[i],((i==n)?" ":" ")); printf("%d ",d[n]); } }