题目链接:https://vjudge.net/problem/UVA-10294

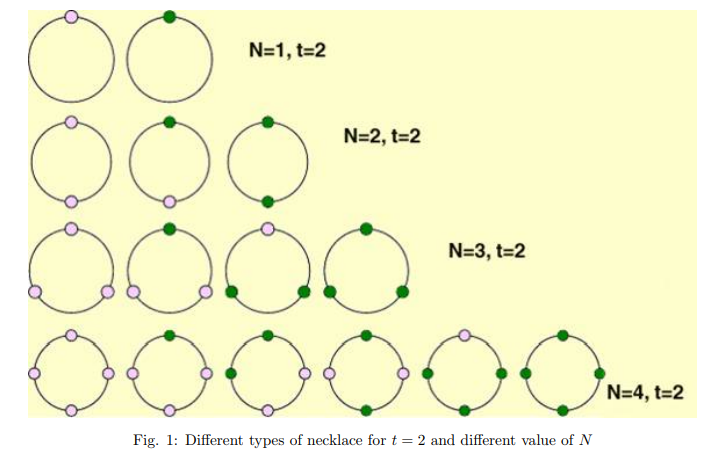
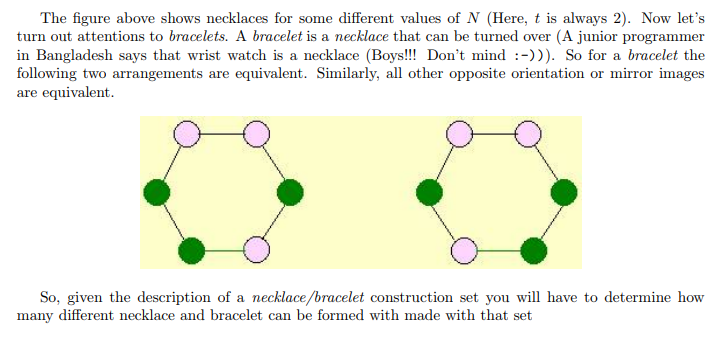

题解:
白书P146~147。
为什么旋转i个间距,就有gcd(i,n)个循环,且每个循环有n/gcd(i,n)个元素?
证明:
(gcd:最大公约数,lcm:最小公倍数)
将珠子从0到n-1标号,对于旋转i位的置换,在以0号为起点,长度为t的一个循环节中,元素标号为:0,i%n,(i*2)%n,…,(i*(t-1))%n
易知:(i*t)%n==0(循环大小为t,跳t次就回到初始点0),即 n*k == i*t,其中n,k,i,t为正整数,因此等式左右的最小值为lcm(n,i),即i*t==lcm(n,i),为什么i*t取最小值,即t取最小值?因为是从0第一次跳到0就完成整个循环的遍历,这个“第一次”就决定了是最早满足条件的那个t,即最小t。
∴ t == lcm(n,i)/i == ( n*i/gcd(n,i) )/i == n/gcd(n,i)
∴ 循环节t==n/gcd(n,i),循环节的个数为:n/t == gcd(n,i)
代码如下:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <vector> 6 #include <cmath> 7 #include <queue> 8 #include <stack> 9 #include <map> 10 #include <string> 11 #include <set> 12 using namespace std; 13 typedef long long LL; 14 const int INF = 2e9; 15 const LL LNF = 9e18; 16 const int MOD = 1e9+7; 17 const int MAXN = 55; 18 19 LL gcd(LL a, LL b) 20 { 21 return b==0?a:gcd(b,a%b); 22 } 23 24 LL Pow[MAXN]; 25 int main() 26 { 27 int n, t; 28 while(scanf("%d%d", &n,&t)!=EOF) 29 { 30 Pow[0] = 1; 31 for(int i = 1; i<=n; i++) Pow[i] = 1LL*Pow[i-1]*t; 32 LL a = 0, b = 0; 33 for(int i = 0; i<n; i++) 34 a += Pow[gcd(i,n)]; 35 if(n%2) 36 b = 1LL*n*Pow[n/2+1]; 37 else 38 b = 1LL*n/2*(Pow[n/2]+Pow[n/2+1]); 39 40 printf("%lld %lld ", a/n, (a+b)/2/n); 41 } 42 }
