图形学基础（二）图形变换_下：3D 平行投影

因为我自己也没太能理解，所以在此就只写一些些。这么多分类，看着就头疼。

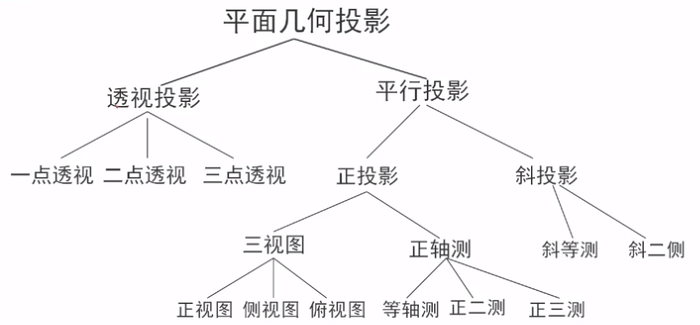
准备（齐次坐标系/图形）

新建BaseClass类（.h .cpp），添加必要的参数和函数。

typedef double array2d[5][5];
typedef double array[24];

class CBaseClass
{
public:int theta_y, phi_x, xx, yy, nn, n;
    array X, Y, Z, C, XT, YT, ZT, XP, YP, ZP, CP;
    array2d A, Ah, Aw;
    double ax[9], ay[9], az[9];
    double bx[9], by[9], bz[9];
public:
    CBaseClass();
    virtual ~CBaseClass();
    void ReadWorkpiece();void Calculate(array2d B);
    void MCalculate(array2d B);
    void XCalculate(array2d B);
    void Drawtext();
    void Display();
    void Draw();
    void Drawve();
    void Drawvt();
    void Drawse();
    void Drawst();
    void DrawViewV(CDC* pdc, CRect rr);
    void DrawViewH(CDC* pdc, CRect rr);
    void DrawViewW(CDC* pdc, CRect rr);

    void moveto(double x, double y, CDC* pdc);
    void lineto(double x, double y, CDC* pdc);
    void cleanMatrice(array2d B);
};

（一些基本函数上一篇给过了，就不再赘述了。另一些辅助函数，用到时再说。）

1、齐次坐标系

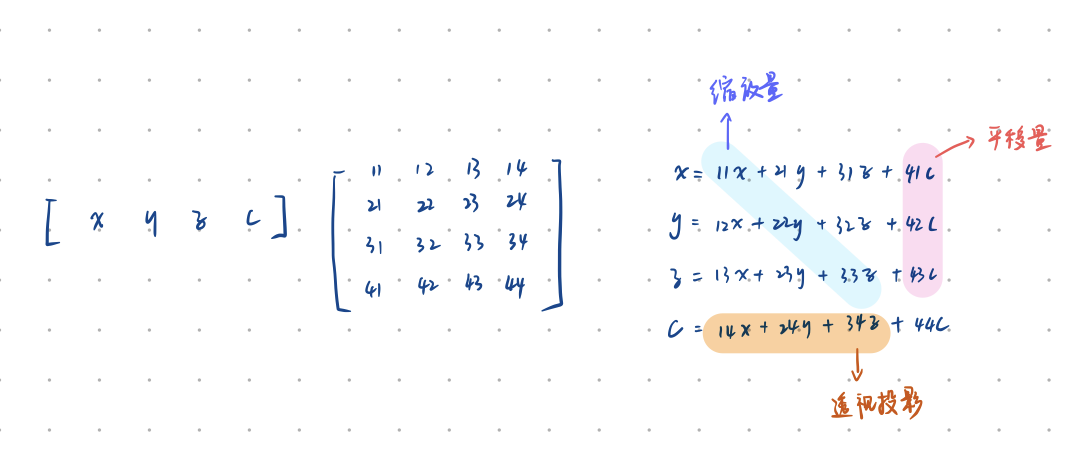
 线代的话，高中水平就够了。齐次坐标系的使用，是为了让平移运算可以和旋转、缩放等运算一起处理。这里不再赘述基本变换。

2、图形

void CBaseClass::ReadWorkpiece()
{
    X[1] = 0; Y[1] = 0; Z[1] = 0; C[1] = 1;
    X[2] = 45; Y[2] = 0; Z[2] = 0; C[2] = 1;
    X[3] = 45; Y[3] = 37; Z[3] = 0; C[3] = 1;
    X[4] = 0; Y[4] = 37; Z[4] = 0; C[4] = 1;
    X[5] = 0; Y[5] = 37; Z[5] = 45; C[5] = 1;
    X[6] = 0; Y[6] = 0; Z[6] = 45; C[6] = 1;
    X[7] = 12; Y[7] = 0; Z[7] = 45; C[7] = 1;
    X[8] = 30; Y[8] = 0; Z[8] = 14; C[8] = 1;
    X[9] = 45; Y[9] = 0; Z[9] = 14; C[9] = 1;
    X[10] = 45; Y[10] = 37; Z[10] = 14; C[10] = 1;
    X[11] = 30; Y[11] = 37; Z[11] = 14; C[11] = 1;
    X[12] = 12; Y[12] = 37; Z[12] = 45; C[12] = 1;
}

三视图

（这里的投影平面和主视图为xoz面。）

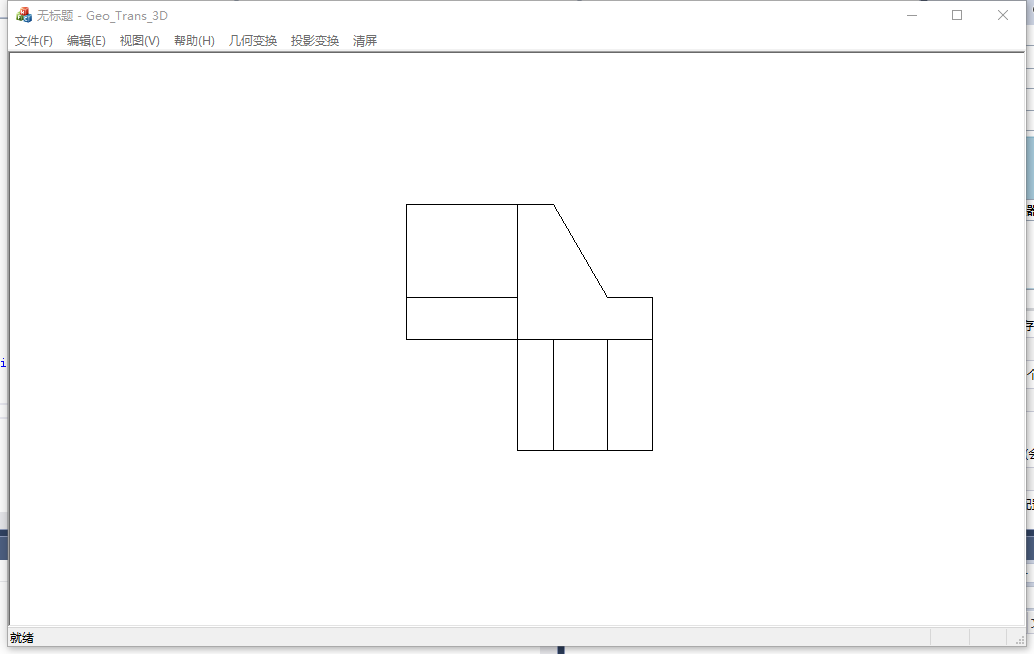
 立体图形（斜二测）和拆解步骤如图：

 

 主视图直接垂直投影；俯视图垂直投影后，绕x轴旋转90°；侧视图垂直投影后，绕z轴旋转90°。

代码如下，已经将俯视图和侧视图的旋转矩阵计算好了。

void CGeoTrans3DView::OnV()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "主视图xoz";
    CBaseClass my;
    my.cleanMatrice(my.A);
    my.A[1][1] = 1;
    my.A[3][3] = 1;
    my.A[4][4] = 1;
    my.Display();
}

void CGeoTrans3DView::OnH()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "俯视图xoy";
    CBaseClass my; 
    my.cleanMatrice(my.Ah);
    my.Ah[1][1] = 1;
    my.Ah[2][3] = -1;
    my.Ah[4][4] = 1;
    my.Display();
}

void CGeoTrans3DView::OnW()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "侧视图yoz";
    CBaseClass my;
    my.cleanMatrice(my.Aw);
    my.Aw[2][1] = -1;
    my.Aw[3][3] = 1;
    my.Aw[4][4] = 1;
    my.Display();
}

 辅助函数 Display()，DrawViewV(CDC * pdc, CRect rr)：

void CBaseClass::Display()
{
    CFrameWnd* pWnd = (CFrameWnd*)AfxGetApp()->m_pMainWnd;
    CDC* pdc = pWnd->GetActiveView()->GetDC();
    CRect rr;
    ::GetClientRect(pWnd->GetActiveView()->m_hWnd, rr);

    DrawViewV(pdc, rr);
    pWnd->GetActiveView()->ReleaseDC(pdc);
}

void CBaseClass::DrawViewV(CDC * pdc, CRect rr)
{
    xx = rr.right / 2;
    yy = rr.bottom / 2;
    Calculate(A);
    moveto(xx + XT[1], yy - ZT[1], pdc);
    for (int I = 2; I <= 12; ++I)
        lineto(xx + XT[I], yy - ZT[I], pdc);
    moveto(xx + XT[1], yy - ZT[1], pdc);
    lineto(xx + XT[4], yy - ZT[4], pdc);
    moveto(xx + XT[1], yy - ZT[1], pdc);
    lineto(xx + XT[6], yy - ZT[6], pdc);
    moveto(xx + XT[7], yy - ZT[7], pdc);
    lineto(xx + XT[12], yy - ZT[12], pdc);
    moveto(xx + XT[3], yy - ZT[3], pdc);
    lineto(xx + XT[10], yy - ZT[10], pdc);
    moveto(xx + XT[2], yy - ZT[2], pdc);
    lineto(xx + XT[9], yy - ZT[9], pdc);
    moveto(xx + XT[12], yy - ZT[12], pdc);
    lineto(xx + XT[5], yy - ZT[5], pdc);
    moveto(xx + XT[8], yy - ZT[8], pdc);
    lineto(xx + XT[11], yy - ZT[11], pdc);
}

轴测投影（正轴测/斜轴测）

轴测投影放弃了可度量性，但增加了一定的真实感（透视图的真实感最强，但我没搞懂...）。它的原理，就是让我们看到一个物体的尽可能多的面。我们在立体几何题目中遇到的图形，一般是斜二测投影得来的，所以我只会画斜二测...

正等轴测图，X,Y,Z三个轴之间的角度是120°,并且三个轴的轴向伸缩系数都是1。

斜二轴测图，X,Y轴之间的角度是135°,X,Z轴之间的角度是90°,Y,Z轴之间的角度是135°,且Y轴的轴向伸缩率为0.5,X,Z轴的轴向伸缩率为1。

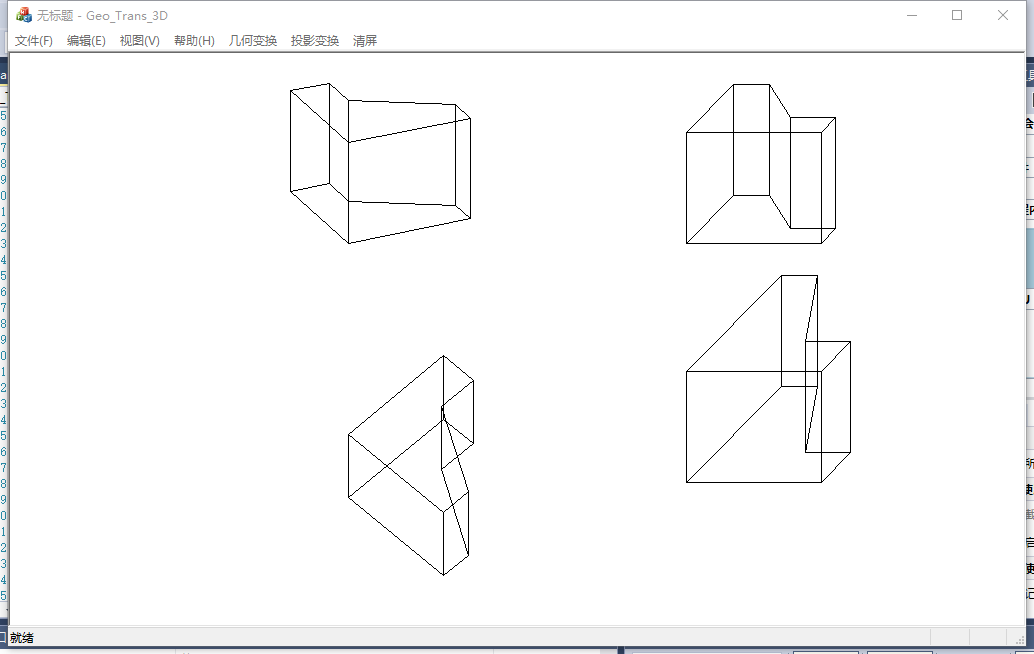
1、正轴测

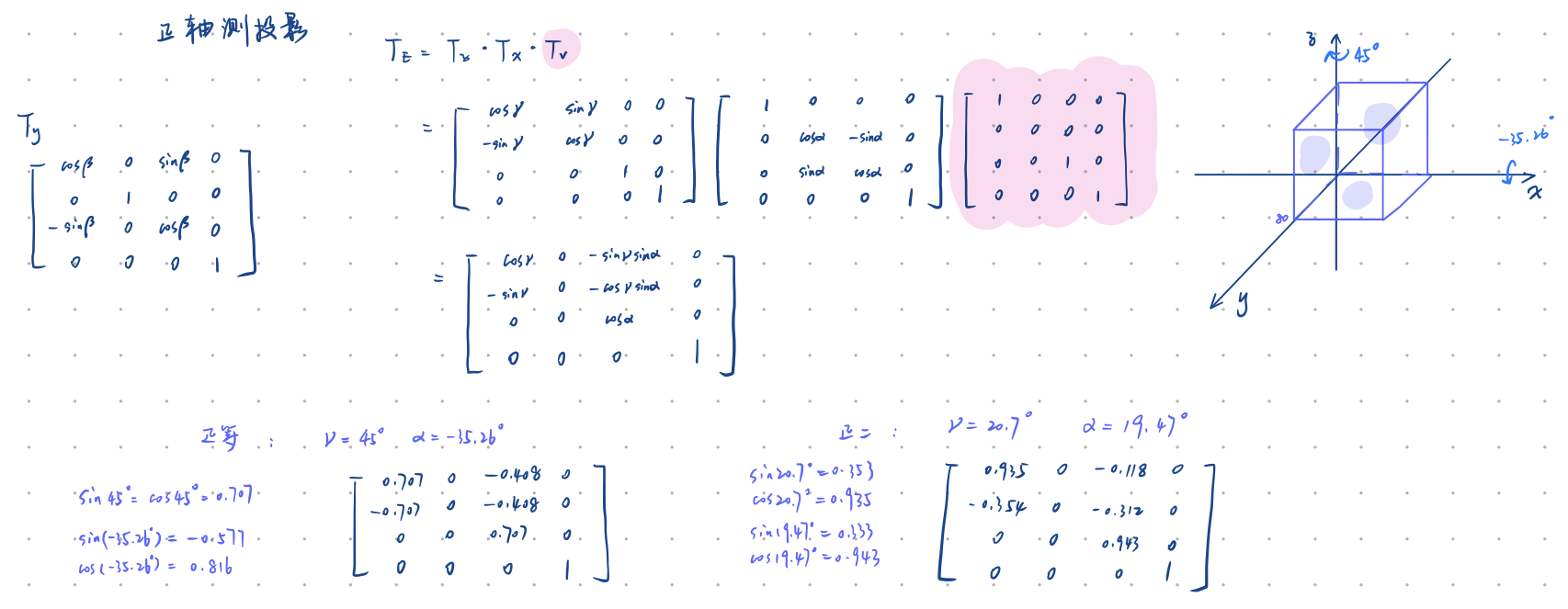
 正等测和正二测，在原理上的区别是Tv，即正等测视图，在旋转后垂直投影即可；正二测旋转后，还需在一个轴向上调整观察位置。。。我在说啥？轻点喷orz。

 同理，可推正三测。

void CGeoTrans3DView::OnVe()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "正等侧图";
    CBaseClass my;
    my.theta_y = 45;//Y轴夹角
    my.phi_x = 125;//X轴夹角
    my.cleanMatrice(my.A);
    my.A[1][1] = (float)cos(my.theta_y*PI / 180);
    my.A[1][2] = (float)sin(my.theta_y*PI / 180)*(float)sin(my.phi_x*PI / 180);
    my.A[2][2] = (float)cos(my.phi_x*PI / 180);
    my.A[3][1] = (float)sin(my.theta_y*PI / 180);
    my.A[3][2] = (float)-cos(my.theta_y*PI / 180)*(float)sin(my.phi_x*PI / 180);
    my.A[4][4] = 1;
    my.Drawve();
}


void CGeoTrans3DView::OnVt()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "正二侧图";
    CBaseClass my;
    my.theta_y = 115;//Y轴夹角
    my.phi_x = 25;//X轴夹角
    my.cleanMatrice(my.A);
    my.A[1][1] = (float)cos(my.theta_y*PI / 180);
    my.A[1][2] = (float)sin(my.theta_y*PI / 180)*(float)sin(my.phi_x*PI / 180);
    my.A[2][2] = (float)cos(my.phi_x*PI / 180);
    my.A[3][1] = (float)sin(my.theta_y*PI / 180);
    my.A[3][2] = (float)-cos(my.theta_y*PI / 180)*(float)sin(my.phi_x*PI / 180);
    my.A[4][4] = 1;
    my.Drawvt();
}

 辅助函数 Drawve()（Drawvt() 一样，只是换了个位置）：

void CBaseClass::Drawve()
{
    int I;
    CFrameWnd* pWnd = (CFrameWnd*)AfxGetApp()->m_pMainWnd;
    CDC* pdc = pWnd->GetActiveView()->GetDC();
    CRect rr;
    ::GetClientRect(pWnd->GetActiveView()->m_hWnd, rr);
    xx = rr.right / 3;
    yy = rr.bottom * 2 / 3;
    MCalculate(A);
    Drawtext();
    moveto(xx + XT[1], yy - YT[1], pdc);
    for (I = 2; I <= 12; ++I)
        lineto(xx + XT[I], yy - YT[I], pdc);
    moveto(xx + XT[1], yy - YT[1], pdc);
    lineto(xx + XT[4], yy - YT[4], pdc);
    moveto(xx + XT[1], yy - YT[1], pdc);
    lineto(xx + XT[6], yy - YT[6], pdc);
    moveto(xx + XT[7], yy - YT[7], pdc);
    lineto(xx + XT[12], yy - YT[12], pdc);
    moveto(xx + XT[3], yy - YT[3], pdc);
    lineto(xx + XT[10], yy - YT[10], pdc);
    moveto(xx + XT[2], yy - YT[2], pdc);
    lineto(xx + XT[9], yy - YT[9], pdc);
    moveto(xx + XT[12], yy - YT[12], pdc);
    lineto(xx + XT[5], yy - YT[5], pdc);
    moveto(xx + XT[8], yy - YT[8], pdc);
    lineto(xx + XT[11], yy - YT[11], pdc);
    pWnd->GetActiveView()->ReleaseDC(pdc);
}

2、斜轴测

（投影方向不垂直于投影平面。）

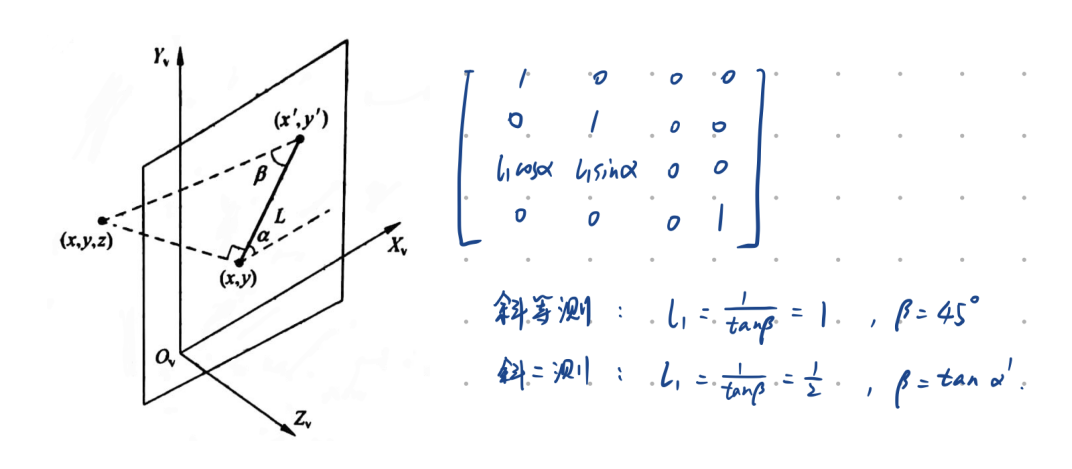
 转换到矩阵上，即错切。

void CGeoTrans3DView::OnSe()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "斜等侧图";
    CBaseClass my;
    my.cleanMatrice(my.A);
    my.A[1][1] = 1;
    my.A[2][2] = 1;    
    my.A[3][1] = 0.707f;//X方向错切
    my.A[3][2] = 0.707f;//Y方向错切
    my.A[4][4] = 1;
    my.Drawse();
}

void CGeoTrans3DView::OnSt()
{
    // TODO: 在此添加命令处理程序代码
    //m_str = "斜二侧图";
    CBaseClass my;
    my.cleanMatrice(my.A);
    my.A[1][1] = 1;
    my.A[2][2] = 1;
    my.A[3][1] = 0.3535f;//X方向错切
    my.A[3][2] = 0.3535f;//Y方向错切
    my.A[4][4] = 1;
    my.Drawst();
}

辅助函数：Drawse()，Drawst() 和 Drawve() 一样，只是换了个位置

参考资料：

1、《计算机图形学原理及算法教程》和青芳 编著

2、计算机图形学 - 中国农业大学 赵明老师视频 

本文采用CC BY 4.0知识共享许可协议。