· 题意
对于一个DAG,在图中任意添加一条边,求可形成的树形图个数。
· 题解
首先对于一个DAG,它们可形成的树形图的个数显然是各点入度相乘。
那么现在加入了一条边,可能会构成环,于是可以用总方案数减去不合法方案数(即构成环的方案数)。
本题解题的关键在于如何构造不合法方案,那么y -> x的所有路径都是不合法的,因为这样一定会构成一个环,那么此时其它的点无论怎么选都是不合法的,应当删去。
于是有

这个时候还要想到DP,不然可能会仅局限于环内那几个点,这样子就不好处理了,此时

那么可以得到转移方程

表示从可到达$i$的$j$转移过来,此时i已经不再是不属于集合$S$的点,所以应当除以其$degree$。
初值
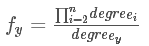
于是拓扑一下就好了。
(以上方程图片均摘自PoPoQQQ)
· 代码

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <queue> 5 6 #define MOD 1000000007 7 8 using namespace std; 9 10 typedef long long LL; 11 12 const int MAXN = 1e05 + 10; 13 const int MAXM = 2e05 + 10; 14 15 struct LinkedForwardStar { 16 int to; 17 18 int next; 19 } ; 20 21 LinkedForwardStar Link[MAXM]; 22 int Head[MAXN]= {0}; 23 int size = 0; 24 25 void Insert (int u, int v) { 26 Link[++ size].to = v; 27 Link[size].next = Head[u]; 28 29 Head[u] = size; 30 } 31 32 LL f[MAXN]; 33 34 int N, M; 35 36 int start, end; 37 38 int temp[MAXN]= {0}, Indeg[MAXN]= {0}; 39 40 LL ans = 1; 41 42 LL inv[MAXM]; 43 44 void Preparation () { 45 inv[1] = 1; 46 for (int i = 2; i <= M + 1; i ++) 47 inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD; 48 } 49 50 queue<int> Que; 51 52 void Toposort () { 53 for (int i = 1; i <= N; i ++) 54 if(! temp[i]) 55 Que.push(i); 56 57 while (! Que.empty()) { 58 int u = Que.front(); 59 Que.pop(); 60 61 f[u] = f[u] * inv[Indeg[u]] % MOD; 62 for (int i = Head[u]; i; i = Link[i].next) { 63 int v = Link[i].to; 64 65 f[v] = (f[v] + f[u]) % MOD; 66 if (temp[v] > 0) { 67 temp[v] --; 68 if (! temp[v]) 69 Que.push(v); 70 } 71 } 72 } 73 } 74 75 int main () { 76 scanf ("%d%d%d%d", & N, & M, & start, & end); 77 78 for (int i = 1; i <= M; i ++) { 79 int u, v; 80 scanf ("%d%d", & u, & v); 81 82 Insert (u, v); 83 temp[v] ++, Indeg[v] ++; 84 } 85 Indeg[end] ++; 86 87 for (int i = 2; i <= N; i ++) 88 ans = ans * Indeg[i] % MOD; 89 90 if (end == 1) { 91 printf ("%lld ", ans); 92 93 return 0; 94 } 95 96 Preparation (); 97 98 f[end] = ans; 99 Toposort (); 100 101 ans = (ans - f[start] + MOD) % MOD; 102 103 printf ("%lld ", ans); 104 105 return 0; 106 } 107 108 /* 109 4 4 4 3 110 1 2 111 1 3 112 2 4 113 3 2 114 */
