Bzoj5332: [Sdoi2018]旧试题

国际惯例的题面

首先我们进行一些相对显然的数学变化。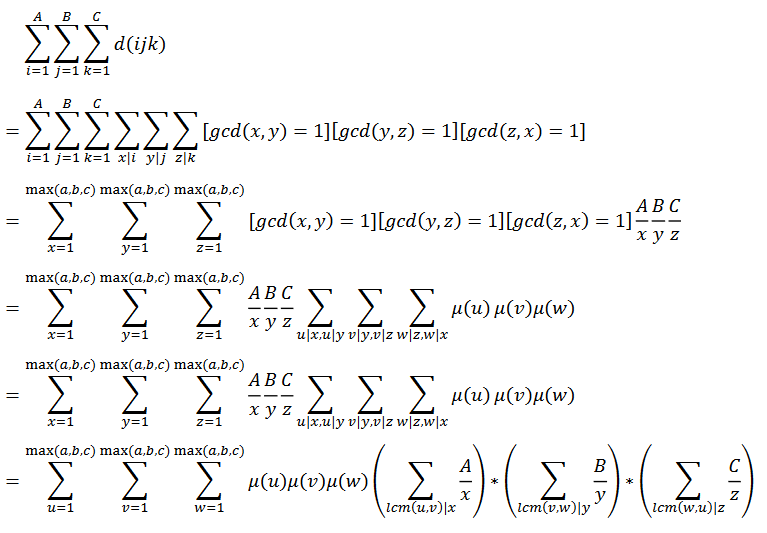

解释一下第二行的那个变形，如果一个数是ijk的因数，那么它一定能被分解成三部分分别是i,j,k的因数。
我们钦定一个质数只能在三部分的一个中出现。如果一个质数仅在ijk中的一个数中出现这样显然是对的，而在多个中出现的话，它贡献答案的次数为它出现的总次数+1次。
而考虑把ijk的乘积分解质因数，然后考虑每个质数的贡献，会发现每个质数贡献答案的次数恰好为它的次数+1次，所以这样是对的。
然后就是分析最后的这个公式了。
右边的三个小求和号里的东西显然可以大力nlog筛预处理一波，这样我们在知道lcm的时候能够O(1)求出这个求和号中的内容。
然后就是前面的东西了。
我们考虑枚举两个数，如果它们的lcm<=max(a,b,c)则相互连边，那么，对答案有贡献的显然就是图中的三元环了。
枚举三元环的话，我们显然有msqrt(m)的算法，其中m为边数。
这种做法就是把双向边都建成单向边，按照度数小的向大的点连或者反之(就像treap大根堆小根堆一样，只要一致了就行)，然后沿着边暴力枚举三个点即可，复杂度就是是msqrt(m)了(别问我证明，我不会QAQ)。
考虑lcm比max(a,b,c)小的数对很少，所以我们这题可以......卡过去。
既然是卡过去显然就要卡常数了......
首先μ为0的数我们显然不用算是吧。
另外直接枚举三元环的细节太多(这题存在自环)，于是我们先单独计算三个数相同的情况和三个数中有两个相同的情况。
存储边用vector存，在大量寻址的时候vector对缓存更加友好。
计算过程不用取模，最后输出再取模，因为答案不会超过long long(虽然听起来很没有道理)，中间即使溢出了也没有关系，只要别溢出超过一轮就行了。
另外最重要的，当你枚举按照边了三个点u,v,w后，是否要计算w和u的lcm来判断两者间是否有边呢？
看起来是需要的，然而并不用！
因为我们连边是存在单调性的，所以我们最终枚举出的三元环一定是u->v->w,u->w的形式。
于是我们在枚举三个点的时候可以先遍历一下u的出边标记下所有可行的w，然后枚举u->v->w之后直接查询lcm就好啦！
于是这样写就跑的飞起了，在BZOJ和洛谷上都是rank1啦。

代码:

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<cctype>
typedef long long int lli;
const int maxn=1e5+1e2,lim=1e5;
const int mod=1e9+7;

struct Edge { int tar,lcm; };
struct Node { int u,v,w; } ns[maxn*21];
int mu[maxn];
lli fa[maxn],fb[maxn],fc[maxn],ans;
int deg[maxn],mem[maxn];
int a,b,c,n,m,ecnt;
std::vector<Edge> es[maxn];

inline int gcd(int x,int y) {
    register int t;
    while( t = x % y ) x = y , y = t;
    return y;
}
inline void sieve() {
    static int prime[maxn/10],cnt;
    static bool vis[maxn];
    mu[1] = 1;
    for(int i=2;i<=lim;i++) {
        if( !vis[i] ) prime[++cnt] = i , mu[i] = -1;
        for(int j=1;j<=cnt&&(lli)i*prime[j]<=lim;j++) {
            const int tar = i * prime[j];
            vis[tar] = 1;
            if( i % prime[j] ) mu[tar] = -mu[i];
            else break;
        }
    }
}

inline void getf(lli* dst,int lim) {
    for(int i=1;i<=lim;i++) for(int j=i;j<=lim;j+=i) dst[i] += lim / j;
}
inline void calc_single_point() {
    for(int i=1;i<=m;i++) if( mu[i] ) ans += mu[i] * mu[i] * mu[i] * fa[i] * fb[i] * fc[i];
}
inline void pre_ring() {
    for(int g=1;g<=n;g++) for(int i=1;i*g<=n;i++) if( mu[i*g] ) for(int j=i+1;(lli)i*j*g<=n;j++) if( mu[j*g] && gcd(i,j) == 1 ) {
        const int u = i * g , v = j * g , w = i * j * g , pi = mu[u] * mu[u] * mu[v] , qi = mu[u] * mu[v] * mu[v];
        if( w > n ) continue;
        ans += pi * ( fa[u] * fb[w] * fc[w] + fa[w] * fb[u] * fc[w] + fa[w] * fb[w] * fc[u] );
        ans += qi * ( fa[v] * fb[w] * fc[w] + fa[w] * fb[v] * fc[w] + fa[w] * fb[w] * fc[v] );
        ++deg[u] , ++deg[v] , ns[++ecnt] = (Node){u,v,w};
    }
    for(int i=1;i<=ecnt;i++) {
        if( deg[ns[i].u] < deg[ns[i].v] || ( deg[ns[i].u] == deg[ns[i].v] && ns[i].u < ns[i].v ) ) es[ns[i].u].push_back((Edge){ns[i].v,ns[i].w});
        else es[ns[i].v].push_back((Edge){ns[i].u,ns[i].w});
    }
}
inline void calc_ring() {
    for(int i=1;i<=n;i++) {
        for(unsigned J=0;J<es[i].size();J++) mem[es[i][J].tar] = es[i][J].lcm;
        for(unsigned J=0;J<es[i].size();J++) {
            const int j = es[i][J].tar;
            for(unsigned K=0;K<es[j].size();K++) {
                const int k = es[j][K].tar , pi = mu[i] * mu[j] * mu[k];
                const int lij = es[i][J].lcm , ljk = es[j][K].lcm , lki = mem[k];
                if( !lki ) continue; // lcm(i,k) > n so i didn't record k .
                ans += pi * ( fa[lij] * fb[ljk] * fc[lki] + fa[lij] * fb[lki] * fc[ljk] + fa[ljk] * fb[lij] * fc[lki] + 
                              fa[ljk] * fb[lki] * fc[lij] + fa[lki] * fb[lij] * fc[ljk] + fa[lki] * fb[ljk] * fc[lij] );
            }
        }
        for(unsigned J=0;J<es[i].size();J++) mem[es[i][J].tar] = 0;
    }    
}

inline void init() {
    n = std::max( a , std::max( b , c ) ) , m = std::min( a , std::min( b , c ) ) , ans = 0;
    memset(fa+1,0,n<<3) , memset(fb+1,0,n<<3) , memset(fc+1,0,n<<3) , memset(deg+1,0,n<<2) , ecnt = 0;
    for(int i=1;i<=n;i++) es[i].clear();
}

inline int getint() {
    int ret = 0 , ch;
    while( !isdigit(ch=getchar()) );
    do ret = ret * 10 + ch - '0'; while( isdigit(ch=getchar()) );
    return ret;
}

int main() {
    static int T;
    T = getint() , sieve();
    while( T-- ) {
        a = getint() , b = getint() , c = getint() , init() , getf(fa,a) , getf(fb,b) , getf(fc,c);
        calc_single_point() , pre_ring() , calc_ring() , printf("%d
",ans%mod);
    }
    return 0;
}

还有两个OJ的rank:

生きてくって多分
只要活着
越えてかなきゃいけないよね
大概就不得不去跨越吧
その勇気で夢の欠片が
鼓起勇气
少しずつ動き出す
一点一点地转动梦的碎片
終わりが始まる
即将迎来终结
何処へ行くのなんて
连目标为何都不知道
わからないまま
就这样迷茫地
ただ過ぎてゆく
度过