快速排序
和归并有些类似,处理上归并是中间分隔处理,快排是找一个random值进行当作基准,然后再两边分开处理,再用递归分治的思路。
从12345-> 123,4,5-> 1,2,3, 4, 5

截取自《算法》
抽象实现
private static void sort(int[] a) { StdRandom.shuffle(e); sort(); } private static void sort(int[] a, int lo, int hi) { if (hi <= lo) { break; } int j = partition(a, lo, hi); sort(a, lo, j - 1); sort(a, j + 1, hi); } private static int partition(int[] a, int lo, int hi) { int i = lo; int j = hi; int v = a[lo]; while (true) { while (less(a[++i], v)) { if (i == hi) { break; } } while (less(v, a[--j])) { if (j == lo) { break; } } if (i >= j) { break; } exch(a, i, j); } exch(a, lo, j); return j; }
1.要原地切分,因为如果自设一个辅助数组,会发生频繁的复制,开销很大。
2.注意越界问题,尤其是切分的基准元素是最大或者最小。
3.保持随机性,这种情况在大数据下验证有明确的性能提升。
4.注意循环的终止。
5.处理与切分元素重复的元素,避免等值元素的交换,这是一种重复元素较少的处理。
6.递归的终止条件。
范例实现
public class QuicklySort { public static void quickSort(int[] s, int l, int r) { if (l < r) { int i = l; int j = r; int x = s[l]; while (i < j) { while (i < j && s[j] > x) { j--; } if (i < j) { s[i] = s[j]; i++; } while (i < j && s[i] < x) { i++; } if (i < j) { s[j] = s[i]; j--; } } s[i] = x; quickSort(s, l, i); quickSort(s, i + 1, r); } }
三向切分快排

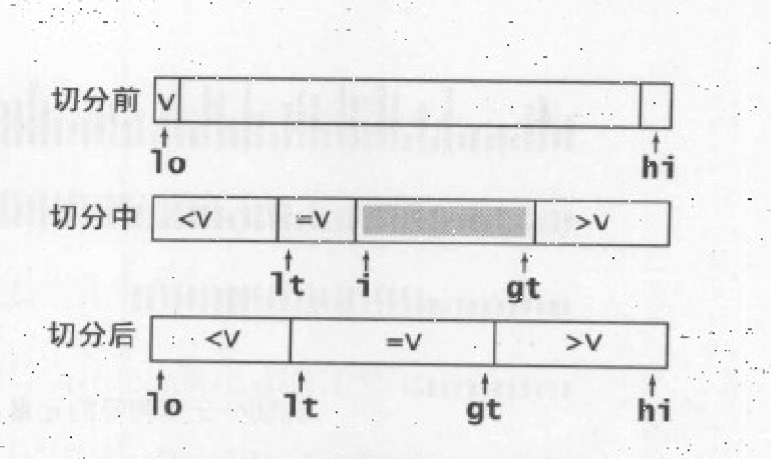
抽象实现
private static void sort3way(int[] a, int lo, int hi) { if (hi <= lo) { return; } int lt = lo; int i = lo + 1; int gt = hi; int v = a[lo]; while (i <= gt) { int comp = a[i].compareTo(v); if (comp < 0) { exch(a, lt++, i++); } else if (comp > 0) { exch(a, i, gt--); } else { i++; } } sort(a, lo, lt - 1); sort(a, gt + 1, hi); }
这算是一种快排的优化,避免了大量重复元素的交换。