对于Hash,我们是怎样来处理冲突的。现在就来介绍一些经典的Hash冲突处理的方法。主要包括
(1)开放地址法
(2)拉链法
(3)再哈希法
(4)建立公共溢出区
(1)开放地址法

(2)拉链法
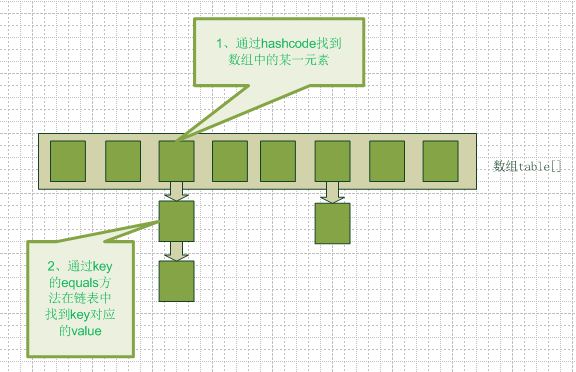
拉链法又叫链地址法,适合处理冲突比较严重的情况。基本思想是把所有关键字为同义词的记录存储在同一个
线性链表中。
(3)再哈希法
再哈希法又叫双哈希法,有多个不同的Hash函数,当发生冲突时,使用第二个,第三个,....,等哈希函数
计算地址,直到无冲突。虽然不易发生聚集,但是增加了计算时间。
(4)建立公共溢出区
建立公共溢出区的基本思想是:假设哈希函数的值域是[1,m-1],则设向量HashTable[0...m-1]为基本
表,每个分量存放一个记录,另外设向量OverTable[0...v]为溢出表,所有关键字和基本表中关键字为同义
词的记录,不管它们由哈希函数得到的哈希地址是什么,一旦发生冲突,都填入溢出表。
经典的hash碰撞面试题:
● 已知一个线性表(38,25,74,63,52,48),假定采用散列函数h(key)=key%7计算散列地址,并散列存储在散列表A[0..6]中,若采用线性探测方法解决冲突,则在该散列表上进行等概率成功查找的平均查找长度为_____2____ 。
若利用拉链法解决冲突,则在该散列表上进行等概率成功查找的平均查找长度为 ___1.33_
解答:
按照H(K)=k mod 7得:
38----1
25----1
74----2
63----1
52----4
48----3
所以ASL=1/6(1+1+2+1+4+3)=2
- 其他回答
- 我们首先必须要知道在建立这个散列表时,每个数据存储时进行了几次散列。这样就知道哪一个元素,查找的长度是多少。
- 散列表的填表 过程如下:
- 首先存入第一个元素38,由于h(38)=38%7=3,又因为3号单元现在没有数据,所以把38存入3号单元。
- 接着存入第二个元素25,由于h(25)=25%7=4,又因为4号单元现在没有数据,所以把25存入4号单元。
- 接着存入第三个元素74,由于h(74)=74%7=4,此时的4号单元已经被25占据,所以进行线性再散列,线性再散列的公式为:Hi= (H(key)+di)% m ,其中的di=1,2,3,4...。所以H1=(4+1)%7=5,此时的单元5没有存数据,所以把74存入到5号单元。
- 接着存入第四个元素63,由于h(63)=63%7=0,此时的0号单元没有数据,所以把63存入0号单元。
- 接着存入第五个元素52,由于h(52)=52%7=3,此时的3号单元已被38占据,所以进行线性再散列:H1=(3+1)%7=4,但4号单元也被占 据了,所以再次散列:H2=(3+2)%7=5,但5号单元也被占据了,所以再次散列:H3=(3+3)%7=6,6号单元为空,所以把52存入6号单 元。
- 最后存入第六个元素48,由于h(48)=48%7=6,此时的6号单元已被占据,所以进行线性再散列:H1=(6+1)%7=0,但0号单元也被占据 了,所以再次散列:H2=(6+2)%7=1,1号单元为空,所以把48存入1号单元。
- 如果一个元素存入时,进行了N次散列,相应的查找次数也是N,所以38,25,63这三个元素的查找长度为1,74的查找长度为2,48的查找长度为 3,52的查找长度为4。所以平均查找长度为:(1+1+1+2+3+4)/6=2。