1、剔除野值点（离群点）
野值点定义为与相应随机变量的中心点相距很远的点，这个距离通常是标准差的整数倍。例如，对于服从正态分布的随机变量，95%的点都在标准差的两倍距离内，而3倍距离则包含了99%的点。
在训练阶段，使用远离平均值的点训练，可能会对学习产生较大的误差，由此影响学习性能。若野值点是噪声时，后果将更加严重，因此剔除野值点是非常有必要的。当野值点较少时，可以将其直接剔除。但是，如果具有长尾分布，那么可以采用对野值点不敏感的代价函数减小其影响。例如，最小平方准则对野值点就非常敏感，因为代价函数中的平方项会产生较大误差。
2、数据归一化
在很多情况下，不同特征值具有不同的动态范围，因此，特征值较大的特征会在代价函数中产生更大影响，但在分类器设计中，特征值的大小并不能反映该特征所重要性。因此使特征位于相似范围作为预处理是非常有必要的，这个操作被称为特征归一化。
（1）一个简单的线性的特征归一化方法是用各自的均值和方差的估计值做归一化，所有归一化后的特征具有零均值和单位方差。具体地，对于第k个特征的N个数据，有
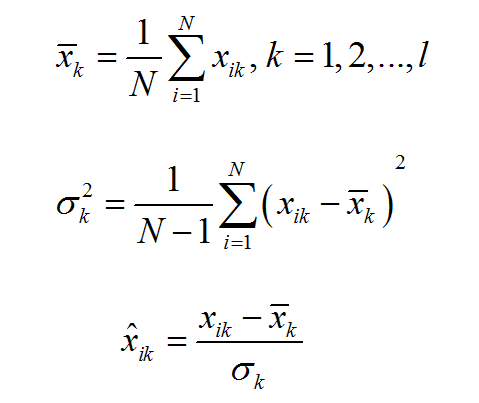
（2）另一个使用较多的线性方法是通过合适的比例将特征值压缩在[0, 1]或[-1,1]范围内。
（3）当数据在均值附近分布不是均匀时，可以使用非线性方法。在这种情况下，使用非线性函数变换将数据映射到指定区间，常见的非线性函数有对数函数、Sigmoid函数等。
Softmax比例是一种常见的将数据限制在[0,1]范围内的非线性压缩方法，它由两步组成:
当
趋近于均值点时，y越趋近于0，因此映射值
越趋近于0.5。而远离均值点时，y值根据标准差和系数r线性变化，其中r值是自定义的，映射值在[0,1]范围内按指数增大或缩小。
3、丢失数据
实际应用中，由于设备采集错误等原因，不同特征的可用数据的个数可能并不相同。如果有足够多训练数据，可以通过剔除一些数据，生成所有特征数量相同的特征向量。但是在许多情况下，直接剔除可用数据是不可行的，在这种情况下，一个常见的做法就是丢失的数据值用相应的均值来代替，而这个均值用相应特征的可用数据计算。而在衡量数据之间相似性时，其中一个常见做法是使用有效特征计算数据数据之间距离。