前言
模拟退火 (Simulated) (Annealing) , 简称 (SA) ,最早在 (1953) 年由 (N. Metropolis) 提出,后经优化得到现在广泛应用的算法,应用在很多领域当中。
算法思想
模拟退火是随机化搜索的一种,若随机化搜索写得好,则可以实现高效率和答案的正确率高(虽说不是 (100\%) )。很多时候在想不出解决办法,或方法的时间复杂度出现极大情况时,可使用模拟退火。所说是有较大几率正确,但还是有疏漏,那么可以多次试验来更加接近准确地求出这个值(还是要看运气)。
模拟退火,顾名思义,是模拟工业上固体降温的过程。先将固体加温到一定的温度后,在按照适当的温度进行冷却,冷却到改物体想要达到的状态。温度降低地越慢,则该物体的质量约高,因为分子在因热加速运动中找到了更加合适的位置。当温度逐渐降低,分子运动减缓,达成目的。
那么这一现象被科学家与计算机算法所联系起来,就成了现在的模拟退火。
网上的一张图,模拟退火可视化:
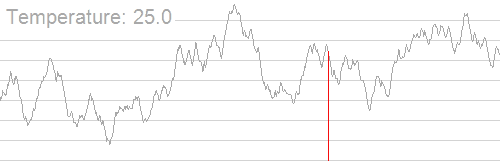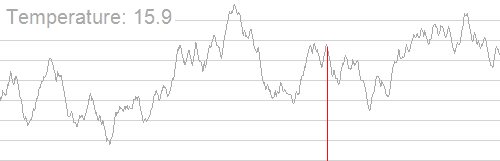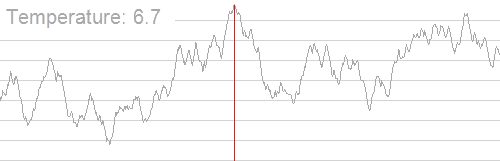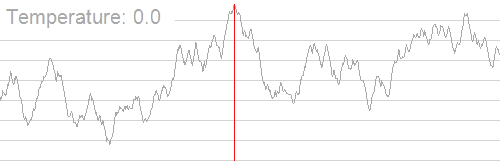
模拟退火有几个很关键的参数,这几个参数决定了模拟退火的优劣。
- 随机种子 (seed) ,可以使用 (19260817) ,或是时间,不推荐使用其他参数,很可能会降低正确率。
- 初始温度 (TempHigh) ,一般取 (100) 至 (10000) 不等,但作者更加倾向于 (2000) 至 (3000) 的数字。
- 目标温度 (TempLow) ,一般取 (1^{-10}) 至 (1^{-15}) 。
- 温度变化率 (TempLess) ,一般取 (0.99) 至 (0.9999) 。建议不取太大,效率不高。
#define Seed 19260817
#define TempLess 0.9975
#define TempHigh 2879.0
#define TempLow 1e-12
来看看降火的主体部分。
void SA() {
double temp = TempHigh;//初始化温度
定义初始状态;
while(temp > TempLow) {//打到降温条件
double nowans = Get_Ans(当前状态);//更新最优解
double diff = nowans - ans;//与当前答案的差值
if(diff > 0) {//比当前答案更优
转移状态;
ans = nowans;//更新答案
}
else if(exp(-diff / temp) * RAND_MAX < rand()) {
//接受这个解,为什么这样写请见例题部分
转移状态;
}
temp *= TempLess;//降温
}
}
模拟退火查询的是多峰函数的最值。
以下曲线是解析式为 (y=0.05x^3-0.5x^2) 的函数的图像:
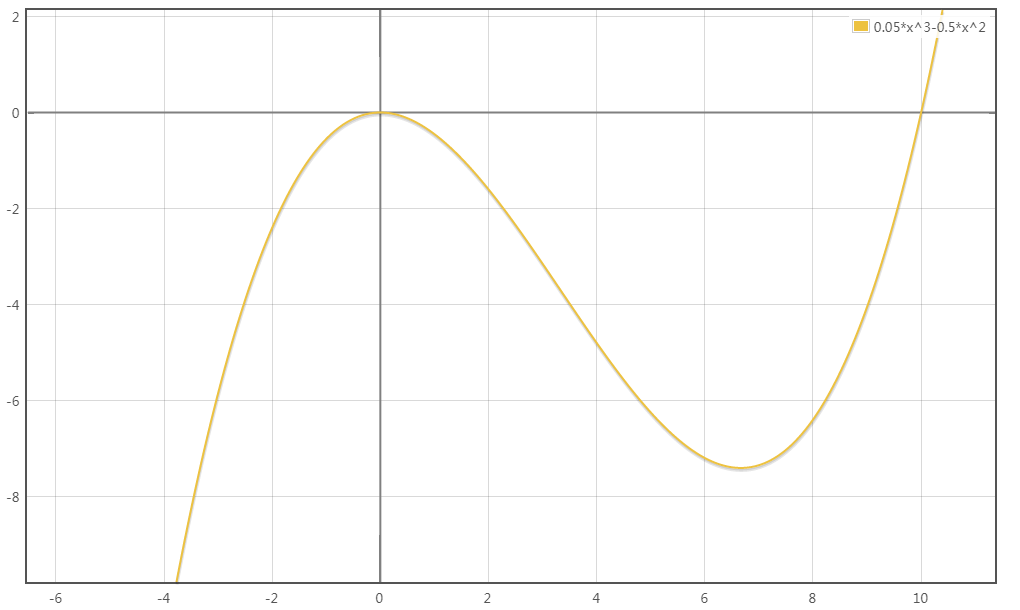
先来考虑贪心的做法:
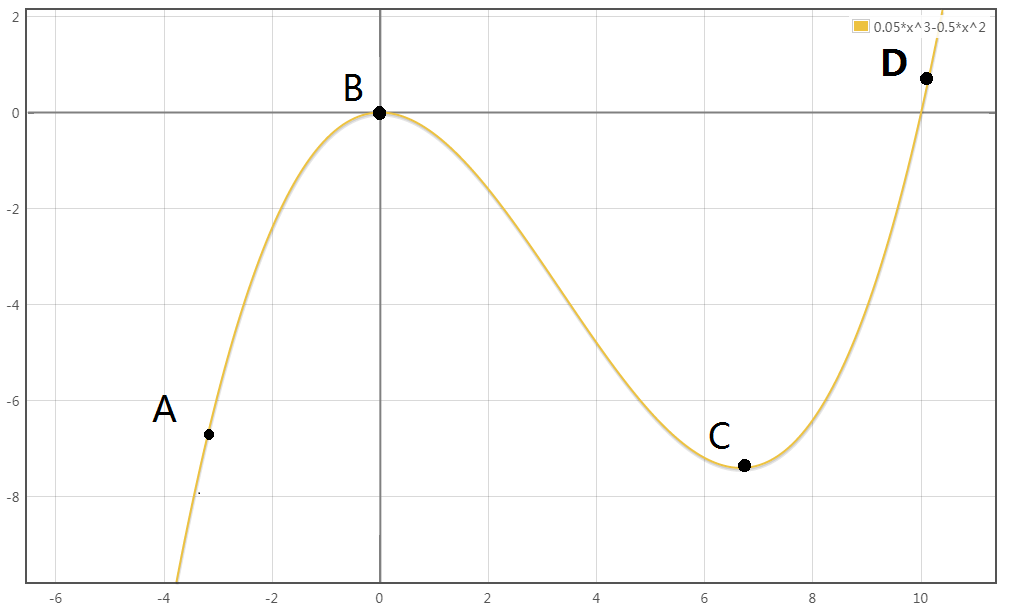
当到达点 (A) 时,程序会选择更高的一个点,那么会从 (A) 点到达 (B) 点,而再从 (B) 点俯瞰,看到了点 (C) ,由于 (C) 的纵坐标比 (B) 小,所以点 (B) 不会到达点 (C) 。换句话说,该程序 (100\%) 不会接受点 (C) ,进而更不会到达点 (D) 。不难发现,这时候找到的局部最优解并不是全局最优解。
而模拟退火再次做出了改进。假设初始位置在点 (A) ,则会基于 (A) 做出左右摆动,经过数次摆动后到达 (B) 。再进一步摆动,假设摆动到了 (C) 点,但是 (C) 的纵坐标比 (B) 小,会以一定几率以 (C) 的纵坐标来接受 (C) 。进而在以同样的方式摆动到点 (D) ,找到更高点。
由于是该算法随机性较高,所以多跑几遍该函数。
下面结合一道例题更加深入地探究,题目链接已在上文给出。
题意
有 (n) 个圆, (m) 个点,请求出一个半径不超过 (r) 的圆,使得与这 (n) 个圆没有交集,且能够覆盖的点最大。
思路
此题的答案圆的圆心并不满足是整数,且由横纵坐标两个值来影响,并不具有规律。这样的问题通常使用模拟退火来解决。
void SA() {
double temp = TempHigh;//初始化温度
定义初始状态;
while(temp > TempLow) {//打到降温条件
double nowans = Get_Ans(当前状态);//更新最优解
double diff = nowans - ans;//与当前答案的差值
if(diff > 0) {//比当前答案更优
转移状态;
ans = nowans;//更新答案
}
else if(exp(-diff / temp) * RAND_MAX < rand()) {//接受这个解
转移状态;
}
temp *= TempLess;//降温
}
}
如上,初始状态包含了横坐标和纵坐标,为了提高正确率与效率,设为所有点的横纵坐标的平均值。
(GetAns) 函数也很简单,先确定半径,半径为这个点到各个圆的切线的距离的最小值,即两个圆心的距离减去当前枚举到的这个圆的半径。后枚举每个点,若这个点被覆盖则 (res++) ,最后返回 (res) 。
double Get_Ans(double x, double y) {
double res = 0;
double rkill = r;
for(int i = 1; i <= n; i++)//枚举圆
rkill = Min(rkill, Dist_Cartesian(XC(i), YC(i), x, y) - RC(i));
for(int i = 1; i <= m; i++)//枚举点
if(Dist_Cartesian(XE(i), YE(i), x, y) <= rkill)
res += 1.0;
return res;
}
有了 (GetAns) 函数,主题部分也很快能出来。
void SA() {
double temp = TempHigh, ansx = initx, ansy = inity;//降温前初始化
while(temp > TempLow) {
double nowx = ansx + ((rand() << 1) - RAND_MAX) * temp;
double nowy = ansy + ((rand() << 1) - RAND_MAX) * temp;
double nowans = Get_Ans(nowx, nowy);
double diff = nowans - ans;
if(diff > 0) {
initx = nowx;
inity = nowy;
ansx = nowx;
ansy = nowy;
ans = nowans;
}
else if(exp(-diff / temp) * RAND_MAX < rand()) {
ansx = nowx;
ansy = nowy;
}
temp *= TempLess;
}
}
首先来看这段代码
double nowx = ansx + ((rand() << 1) - RAND_MAX) * temp;
double nowy = ansy + ((rand() << 1) - RAND_MAX) * temp;
由答案左右摆动,生成新的当前状态 (nowx) 和 (nowy) ,摆动幅度是随机的,应该是由分子做无规则运动而来。乘上 (temp) 当前温度是由分子在越热的环境中,运动得越快而得来。
紧接着两行就是求出当前状态的答案,在求出它与当前最优解的差值。
第一个 (if) 是当前这个局部解大于当前最优解,则用当前最优的局部解来更新最优解。
重点是下一个 (if) ,这行代码就是它与贪心的不同,以一定几率接受这个解,在用它更新当前状态,进行左右摆动,从而找到局部更优解,更加接近整体最优解。其条件的优越性由 (Metropolis) 接受准则给出。也就是 (else) (if) 中的条件:
exp(-diff / temp) * RAND_MAX < rand()
思路整理完了,此题并没有多少思维难度,但是需要对上述几个参数进行调整,可以多总结一些正确率大的参数,以备下次使用
C++代码
#include <cmath>
#include <cstdio>
#include <cstdlib>
#define Min(a, b) ((a) < (b) ? (a) : (b))
#define Seed 19260817//随机种子
#define TempLess 0.9975//温度变化率
#define TempHigh 2879.0//初始温度
#define TempLow 1e-12//目标温度
void Quick_Read(double &N) {//double快速读入
N = 0.0;
double now, wei = 0.1;
bool op = false;
char c = getchar();
while(c < '0' || c > '9') {
if(c == '-')
op = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
N = N * 10.0 + (c ^ 48) * 1.0;
c = getchar();
}
if(c == '.') {
c = getchar();
while(c >= '0' && c <= '9') {
N += (c ^ 48) * wei;
wei /= 10.0;
c = getchar();
}
}
if(op)
N = -N;
}
const int MAXN = 15;
const int MAXM = 1e3 + 5;
struct Circle {//题目中的圆
double Abscissa_C, Ordinate_C, Radius_C;
#define XC(x) buildings[x].Abscissa_C
#define YC(x) buildings[x].Ordinate_C
#define RC(x) buildings[x].Radius_C
};
Circle buildings[MAXN];
struct Enemy {//题目中的点
double Abscissa_E, Ordinate_E;
#define XE(x) foe[x].Abscissa_E
#define YE(x) foe[x].Ordinate_E
};
Enemy foe[MAXM];
double n, m, r;
double initx, inity;//记录答案的横纵坐标
double ans;//答案
double Dist_Cartesian(double XA, double YA, double XB, double YB) {//两点间距离公式
double frontx = (XA - XB) * (XA - XB);
double fronty = (YA - YB) * (YA - YB);
double dist = sqrt(frontx + fronty);
return dist;
}
double Get_Ans(double x, double y) {//找到当前状态的答案
double res = 0;
double rkill = r;
for(int i = 1; i <= n; i++)//求出最大半径
rkill = Min(rkill, Dist_Cartesian(XC(i), YC(i), x, y) - RC(i));
for(int i = 1; i <= m; i++)//求出被圆覆盖的点
if(Dist_Cartesian(XE(i), YE(i), x, y) <= rkill)
res += 1.0;
return res;
}
void SA() {
double temp = TempHigh, ansx = initx, ansy = inity;//初始化
while(temp > TempLow) {//降温
double nowx = ansx + ((rand() << 1) - RAND_MAX) * temp;//当前状态x
double nowy = ansy + ((rand() << 1) - RAND_MAX) * temp;//当前状态y
double nowans = Get_Ans(nowx, nowy);//当前局部答案
double diff = nowans - ans;//当前答案与最优解的差值
if(diff > 0) {//比当前最优解更优则更新最优解
initx = nowx;
inity = nowy;
ansx = nowx;
ansy = nowy;
ans = nowans;
}
else if(exp(-diff / temp) * RAND_MAX < rand()) {
//按照Metropolis接受准则接受改状态
ansx = nowx;
ansy = nowy;
}
temp *= TempLess;//降温
}
}
void Cool_Down() {
int frequ = 6;
while(frequ--)//随机化算法尽量多跑几次
SA();
}
void Make_Seed() {//生成随机种子
srand(Seed);
}
void Read() {//输入
Quick_Read(n);
Quick_Read(m);
Quick_Read(r);
for(int i = 1; i <= n; i++) {
Quick_Read(XC(i));
Quick_Read(YC(i));
Quick_Read(RC(i));
}
for(int i = 1; i <= m; i++) {
Quick_Read(XE(i));
Quick_Read(YE(i));
initx += XE(i);
inity += YE(i);
}
initx /= m;//以平均值开始提高效率与准确率
inity /= m;
}
void Write() {//输出
printf("%.0lf", ans);
}
int main() {
Make_Seed();
Read();
Cool_Down();
Write();
return 0;
}