一、题目
二、解法
势能线段树
常见的套路:我们把询问按右端点离线,对于每个左端点维护其答案。
考虑插入 (a_r) 之后如何维护最小值,想象所有已有的数已经排列在了一个数轴上,我们可以感知到受影响的点数应该不会很多,但是快速找到受影响的点貌似是不可能的。
可以换个思路,我们猜测每个点受影响的次数不会很多,这启示我们对于每个点定义一个势能 (h(x)=log a_x),我们希望每次更新一个点时它的势能可以减少 (1)
带着这个目标来设计更新策略,我们考虑以前 (a_i) 对应的最优点是 (a_j)((i<j)),现在要去更新它:
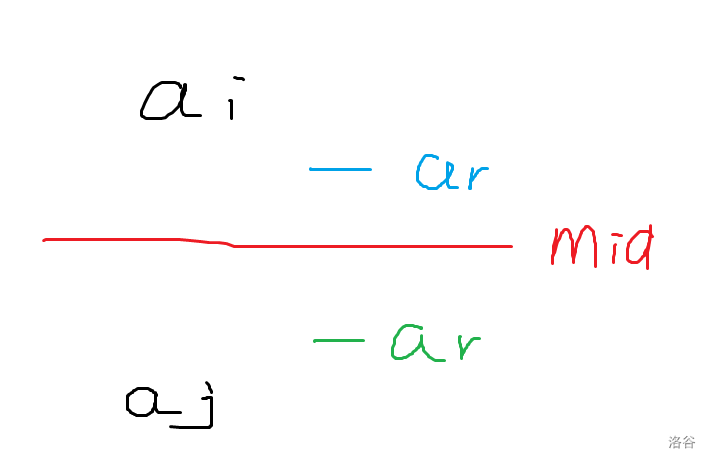
- 如果 (a_r) 在接近 (a_i) 的一侧,那么直接拿去更新 (a_i),势能减少 (1)
- 如果 (a_r) 在接近 (a_j) 的一侧,那么不需要更新 (a_i),因为此时 (a_j) 处的答案一定比 (a_i) 优,而我们每次都是取 ([1,r]) 的一个后缀作为答案,又有 (i<j) 所以不用考虑它了。
线段树的节点上维护一个 ( t set),每次暴力找前驱后继就可以判断子树内是否存在应该被修改的点,我们先访问右子树,再访问左子树,再回溯时记录一下最小值即可。
时间复杂度 (O(nlog^2 nlog a)),但是这东西跟树剖一样很难跑满
补充:更为严谨的势能定义是设左边的最优匹配点是 (a_k),右边的最优匹配点是 (a_j)(按值大小排序),那么 (h(i)=log (a_j-a_i)+log(a_i-a_k))
分块
什么都要卡,草,这题必须疯狂前缀最小值,写麻了。
现在你知道写什么了吧,虽然我还是会贴一个分块代码
#include <cstdio>
#include <algorithm>
#include <set>
using namespace std;
const int M = 400005;
const int inf = 0x3f3f3f3f;
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,cur,a[M],mi[M],ans[M];set<int> s[M];
struct node
{
int l,r,id;
bool operator < (const node &b) const
{
return r<b.r;
}
}q[M];
void build(int i,int l,int r)
{
mi[i]=inf;
for(int p=l;p<=r;p++)
s[i].insert(a[p]);
if(l==r) return ;
int mid=(l+r)>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
}
void upd(int i,int l,int r,int L,int R,int c)
{
if(L>r || l>R) return ;
if(L<=l && r<=R)
{
set<int>::iterator it=s[i].lower_bound(c);
if(it!=s[i].end()) mi[i]=min(mi[i],*it-c);
if(it!=s[i].begin()) it--,mi[i]=min(mi[i],c-*it);
if(mi[i]>=cur) return ;
}
if(l==r)
{
cur=min(cur,mi[i]);
return ;
}
int mid=(l+r)>>1;
upd(i<<1|1,mid+1,r,L,R,c);
upd(i<<1,l,mid,L,R,c);
mi[i]=min(mi[i<<1],mi[i<<1|1]);
cur=min(cur,mi[i]);
}
int ask(int i,int l,int r,int L,int R)
{
if(L>r || l>R) return inf;
if(L<=l && r<=R) return mi[i];
int mid=(l+r)>>1;
return min(ask(i<<1,l,mid,L,R),
ask(i<<1|1,mid+1,r,L,R));
}
signed main()
{
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
build(1,1,n);
m=read();
for(int i=1;i<=m;i++)
q[i].l=read(),q[i].r=read(),q[i].id=i;
sort(q+1,q+1+m);
for(int i=1,j=1;i<=n;i++)
{
cur=inf;
upd(1,1,n,1,i-1,a[i]);
while(j<=m && q[j].r<=i)
{
ans[q[j].id]=ask(1,1,n,q[j].l,q[j].r);
j++;
}
}
for(int i=1;i<=m;i++)
printf("%d
",ans[i]);
}
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int M = 100005;
const int N = 560;
const int inf = 2e9;
#define pii pair<int,int>
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m,k,b,cl[M],bl[N],br[N],f[N][N],g[M][N];
vector<pii> s[N];pii a[M];vector<int> v[N];
int Abs(int x) {return x>0?x:-x;}
int merge(vector<int> &a,vector<int> &b)
{//merge to get the min |x-y|
int l1=a.size(),l2=b.size(),i=0,j=0,res=inf;
for(int i=1;i<l1;i++) res=min(res,a[i]-a[i-1]);
for(int i=1;i<l2;i++) res=min(res,b[i]-b[i-1]);
while(i<l1 && j<l2)
{
res=min(res,Abs(a[i]-b[j]));
if(a[i]<b[j]) i++;else j++;
}
return res;
}
void write(int x)
{
if(x<=9)
{
putchar(x+'0');
return ;
}
write(x/10);
putchar(x%10+'0');
}
signed main()
{
n=read();b=sqrt(n);
for(int i=1;i<=n;i++)
{
a[i]=make_pair(read(),i);
cl[i]=(i-1)/b+1;
s[cl[i]].push_back(a[i]);
if(!bl[cl[i]]) bl[cl[i]]=i;
br[cl[i]]=i;
}
k=cl[n];
//block&block / within block
for(int i=1;i<=k;i++)
{
sort(s[i].begin(),s[i].end());
for(auto x:s[i]) v[i].push_back(x.first);
}
for(int i=1;i<=k;i++)
{
f[i][i]=inf;
for(int j=1;j<s[i].size();j++)
f[i][i]=min(f[i][i],s[i][j].first-s[i][j-1].first);
for(int j=i+1;j<=k;j++)
{
f[i][j]=merge(v[i],v[j]);
if(j>i) f[i][j]=min(f[i][j-1],f[i][j]);
}
}
//block and element
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)
g[i][cl[i]]=inf;
for(int p=1;p<=k;p++)
{
int l=s[p].size();
for(int i=1,j=0;i<=n;i++)
{
int id=a[i].second;g[id][p]=inf;
while(j<l && s[p][j]<a[i]) j++;
if(j<l) g[id][p]=Abs(a[i].first-s[p][j].first);
if(j) g[id][p]=min(g[id][p],
Abs(a[i].first-s[p][j-1].first));
}
}
for(int p=1;p<=k;p++)
{
for(int i=bl[p];i<=br[p];i++)
{
for(int j=p-2;j>=1;j--)
g[i][j]=min(g[i][j+1],g[i][j]);
for(int j=p+2;j<=k;j++)
g[i][j]=min(g[i][j],g[i][j-1]);
}
for(int j=1;j<p;j++)
for(int i=bl[p]+1;i<=br[p];i++)
g[i][j]=min(g[i][j],g[i-1][j]);
for(int j=p+1;j<=k;j++)
for(int i=br[p]-1;i>=bl[p];i--)
g[i][j]=min(g[i][j],g[i+1][j]);
}
for(int r=1;r<=k;r++)
for(int l=r-1;l>=1;l--)
f[l][r]=min(f[l][r],f[l+1][r]);
//query
m=read();
while(m--)
{
int l=read(),r=read(),ans=inf;
if(cl[l]==cl[r])//in the same block
{
int ls=-1;
for(auto x:s[cl[l]])
if(x.second>=l && x.second<=r)
{
if(ls>0) ans=min(ans,x.first-ls);
ls=x.first;
}
write(ans);puts("");
continue;
}
if(cl[l]+1<cl[r]) ans=f[cl[l]+1][cl[r]-1],
ans=min(ans,min(g[r][cl[l]+1],g[l][cl[r]-1]));
vector<int> n1,n2;
for(auto x:s[cl[l]])
if(x.second>=l) n1.push_back(x.first);
for(auto x:s[cl[r]])
if(x.second<=r) n2.push_back(x.first);
ans=min(ans,merge(n1,n2));
write(ans);puts("");
}
}