一、题目
二、解法
根据随机增量法的复杂度分析,我们发现就算在高维情况它也是 (O(n)) 的,问题在于 (m) 维空间,给定 (k+1) 个在圆上的点,怎么求覆盖它们的最小圆?可以考虑高斯消元,但要推柿子。
结论:最小圆的圆心一定要在这 (k+1) 个点构成的平面上,也就是说以某个点为原点构建出 (k) 个向量基底,圆心要能被这 (k) 个基底表示出来,因为这样圆的半径才能最小,翻译成数学语言,设向量 (x) 为圆心,(x_i) 表示给定的点:
[x-x_0=sum_{i=1}^k w_i(x_i-x_0)
]
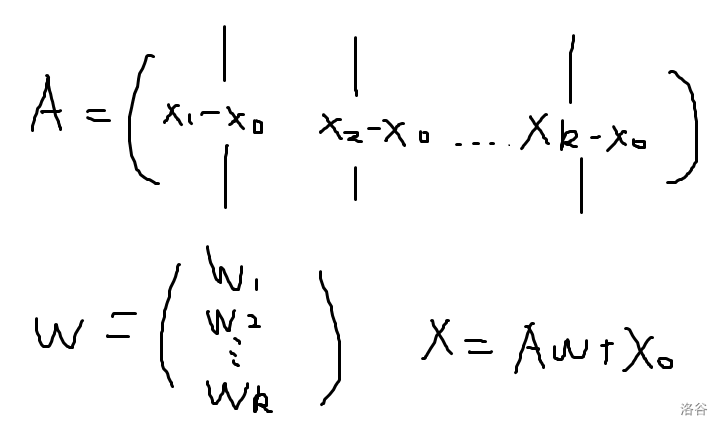
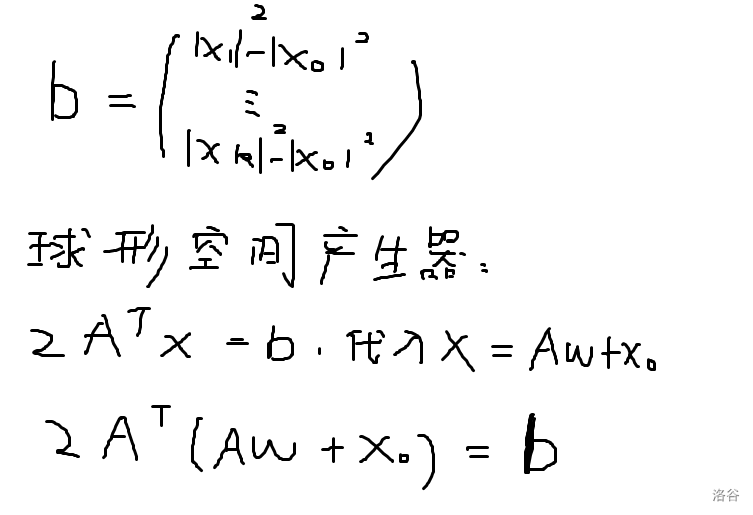
[2A^TAw=b-2A^Tx_0
]
现在就可以直接算了,如果你喜欢还可以化简成下面的形式:
[(b-2A^Tx_0)_i=|x_i|^2-|x_0|^2-2x_i^Tcdot x_0+2|x_0|^2=|x_i-x_0|^2
]
(2A^TA) 就是我们的系数矩阵,(|x_i-x_0|^2) 是等号右边的东西,解出来 (w) 向量就可以算出圆心坐标了。
三、总结
由于最小圆覆盖的复杂度证明它在高维情况下也适用。
推柿子的时候可以把向量写成矩阵的形式。
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <ctime>
using namespace std;
const int M = 20005;
#define db double
#define eps 1e-7
int read()
{
int x=0,f=1;char c;
while((c=getchar())<'0' || c>'9') {if(c=='-') f=-1;}
while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int n,m;db r;
struct point
{
db x[6];
point() {for(int i=0;i<m;i++) x[i]=0;}
point operator + (point b)
{
point r;
for(int i=0;i<m;i++)
r.x[i]=x[i]+b.x[i];
return r;
}
point operator - (point b)
{
point r;
for(int i=0;i<m;i++)
r.x[i]=x[i]-b.x[i];
return r;
}
point operator * (db t)
{
point r;
for(int i=0;i<m;i++)
r.x[i]=x[i]*t;
return r;
}
db len()
{
db r=0;
for(int i=0;i<m;i++)
r+=x[i]*x[i];
return r;
}
}p[M],e[9],o;
db sqr(db x) {return x*x;}
db Abs(db x) {return x>0?x:-x;}
point cir(int n)
{
db a[9][9]={},b[9][9]={},c[9][9]={};
if(n==0) return e[0];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
a[i][j]=b[j][i]=e[i].x[j-1]-e[0].x[j-1];
c[i][n+1]+=sqr(e[i].x[j-1]-e[0].x[j-1]);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=n;k++)
c[i][k]+=a[i][j]*b[j][k];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c[i][j]*=2;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
if(Abs(c[i][i])<eps && Abs(c[j][i])>eps)
{
swap(c[i],c[j]);
break;
}
for(int j=1;j<=n;j++)
{
if(Abs(c[j][i])<eps || i==j) continue;
db t=c[j][i]/c[i][i];
for(int k=1;k<=n+1;k++)
c[j][k]-=t*c[i][k];
}
}
point r=e[0];
for(int i=1;i<=n;i++)
r=r+(e[i]-e[0])*(c[i][n+1]/c[i][i]);
return r;
}
void dfs(int u,int v,int lim)
{
if(v==lim) return ;
if((p[v]-o).len()>r)
{
e[u]=p[v];
o=cir(u);r=(p[v]-o).len();
if(u<m) dfs(u+1,0,v);//adjust from begin
}
dfs(u,v+1,lim);//move on
}
signed main()
{
n=read();m=read();
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
scanf("%lf",&p[i].x[j]);
random_shuffle(p,p+n);
dfs(0,0,n);
for(int i=0;i<m;i++)
printf("%.8f ",o.x[i]);
}