邻接矩阵、度矩阵 Learner

邻接矩阵（Adjacency）

     邻接矩阵表示顶点间关系，是 n 阶方阵（n为顶点数量）。
     邻接矩阵分为有向图邻接矩阵和无向图邻接矩阵。无向图邻接矩阵是对称矩阵，而有向图的邻接矩阵不一定对称。

　　　　$[A(\mathcal{G})]_{i j}=\left\{\begin{array}{l}1 \text { if } v_{i} v_{j} \in E \\0 \text { otherwise }\end{array}\right.$

度矩阵（Degree）

     度矩阵是对角阵，对角上的元素为各个顶点的度。顶点 $v_i$ 的度表示和该顶点相关联的边的数量。
     无向图中顶点 $v_i$ 的度 $d(v_i)=N(i)$。

　　　　　　

 

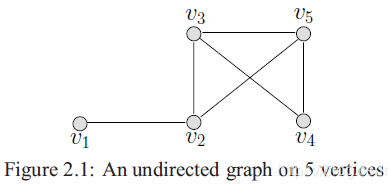
　　Figure 2.1 的度矩阵和邻接矩阵如下：

　　　　

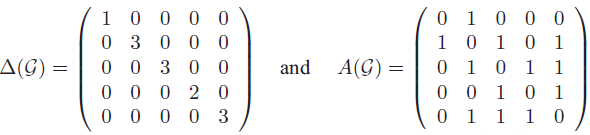
　　$A=D^{-1} S$，其中D是度矩阵，S是邻接矩阵。

　　度矩阵的逆刚好是其数值的倒数，乘以矩阵等于该度矩阵的水平方向的平均值，加起来等于一。乘以节点输入层相当于对其做了各平均，避免计算过程中数值过大（邻接节点的和）。

import numpy as np
Degree = np.array([[1,0, 0,0,0], [0,3, 0,0,0],[0,0, 3,0,0],[0,0, 0,2,0],[0,0, 0,0,3],])
Adj = np.array([[0,1, 0,0,0], [1,0, 1,0,1],[0,1, 0,1,1],[0,0, 1,0,1],[0,1, 1,1,0],])
invD = np.linalg.inv(Degree)
print("invD =\n",invD )
print("Adj =\n",Adj )
print("np.matmul(invD,A) =\n",np.matmul(invD,Adj))

结果：

invD =
[[1. 0. 0. 0. 0. ]
[0. 0.33333333 0. 0. 0. ]
[0. 0. 0.33333333 0. 0. ]
[0. 0. 0. 0.5 0. ]
[0. 0. 0. 0. 0.33333333]]
Adj =
[[0 1 0 0 0]
[1 0 1 0 1]
[0 1 0 1 1]
[0 0 1 0 1]
[0 1 1 1 0]]
np.matmul(invD,A) =
[[0. 1. 0. 0. 0. ]
[0.33333333 0. 0.33333333 0. 0.33333333]
[0. 0.33333333 0. 0.33333333 0.33333333]
[0. 0. 0.5 0. 0.5 ]
[0. 0.33333333 0.33333333 0.33333333 0. ]]