Pytorch 实现简单线性回归
问题描述:
使用 pytorch 实现一个简单的线性回归。
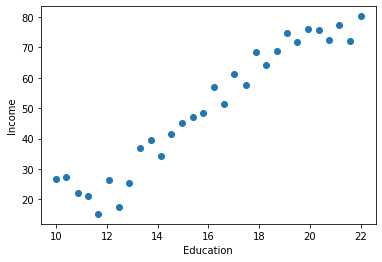
受教育年薪与收入数据集
单变量线性回归
单变量线性回归算法(比如,$x$ 代表学历,$f(x)$ 代表收入):
$f(x) = w*x + b $
我们使用 $f(x)$ 这个函数来映射输入特征和输出值。
目标:
预测函数 $f(x)$ 与真实值之间的整体误差最小。
损失函数:
使用均方差作为作为成本函数。
也就是预测值和真实值之间差的平方取均值。
成本函数与损失函数:
优化的目标( $y$ 代表实际的收入):
找到合适的 $w$ 和 $b$ ,使得 $(f(x) - y)^{2}$越小越好
注意:现在求解的是参数 $w$ 和 $b$。
过程
1 导入实验所需要的包
import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from torch import nn
#解决内核挂掉
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
2 读取数据
data = pd.read_csv('dataset/Income1.csv')
print(type(data))
<class 'pandas.core.frame.DataFrame'>
3 查看数据信息
data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 30 entries, 0 to 29
Data columns (total 3 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Unnamed: 0 30 non-null int64
1 Education 30 non-null float64
2 Income 30 non-null float64
dtypes: float64(2), int64(1)
memory usage: 848.0 bytes
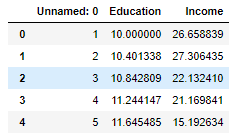
查看数据
data
查看数据类型
type(data.Education)
pandas.core.series.Series
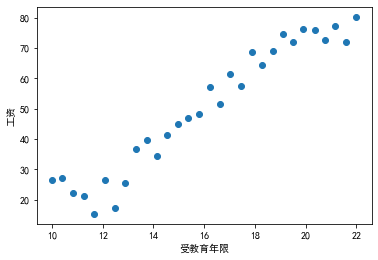
4 图表显示数据from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 雅黑字体
plt.scatter(data.Education,data.Income)
plt.xlabel("受教育年限")
plt.ylabel("工资")
plt.show()
5 转换数据为 Tensor 类型
查看特征数据
data.Education
0 10.000000
1 10.401338
2 10.842809
3 11.244147
4 11.645485
5 12.086957
6 12.488294
7 12.889632
查看特征数据 index
data.Education.index
RangeIndex(start=0, stop=30, step=1)
查看特征数据 value
data.Education.values
array([10. , 10.40133779, 10.84280936, 11.24414716, 11.64548495,
12.08695652, 12.48829431, 12.88963211, 13.2909699 , 13.73244147,
14.13377926, 14.53511706, 14.97658863, 15.37792642, 15.77926421,
16.22073579, 16.62207358, 17.02341137, 17.46488294, 17.86622074,
18.26755853, 18.7090301 , 19.11036789, 19.51170569, 19.91304348,
20.35451505, 20.75585284, 21.15719064, 21.59866221, 22. ])
特征数据变换形状
data.Education.values.reshape(-1,1)
array([[10. ],
[10.40133779],
[10.84280936],
[11.24414716],
[11.64548495],
[12.08695652],
[12.48829431],
[12.88963211],
[13.2909699 ],
[13.73244147],
[14.13377926],
[14.53511706],
[14.97658863],
[15.37792642],
[15.77926421],
[16.22073579],
[16.62207358],
[17.02341137],
[17.46488294],
[17.86622074],
[18.26755853],
[18.7090301 ],
[19.11036789],
[19.51170569],
[19.91304348],
[20.35451505],
[20.75585284],
[21.15719064],
[21.59866221],
[22. ]])
查看特征数据变换后的形状
data.Education.values.reshape(-1,1).shape
查看特征数据变换后的数据类型
type(data.Education.values.reshape(-1,1))
numpy.ndarray
修改特征数据变换后的数据类型
X = data.Education.values.reshape(-1,1).astype(np.float32)
print(type(X))
X.shape
特征数据和标签转换为Tensor
X = torch.from_numpy(data.Education.values.reshape(-1,1).astype(np.float32) ) #转换数据类型
Y = torch.from_numpy(data.Income.values.reshape(-1,1).astype(np.float32) ) #转换数据类型
6 定义模型
定义线性回归模型:
model = nn.Linear(1,1) #w@input+b 等价于model(input)
定义均方损失函数
loss_fn = nn.MSELoss() #定义均方损失函数
定义优化器
opt = torch.optim.SGD(model.parameters(),lr=0.00001)
7 模型训练
for epoch in range(200):
for x, y in zip(X,Y):
y_pred = model(x) #使用模型预测
loss = loss_fn(y,y_pred) #根据预测计算损失
opt.zero_grad() #进行梯度清零
loss.backward() #求解梯度
opt.step() #优化模型参数
8 输出权重和偏置
model.weight
model.bias
Tensor 类型数据带梯度转换为numpy需要先去梯度
type(model.weight.detach().numpy())
numpy.ndarray
9 获取预测值 y_pred
model(X).data.numpy()
预测值类型
type(model(X).data.numpy())
numpy.ndarray
预测值size
model(X).data.numpy().shape
(30, 1)
10 绘制回归曲线
plt.scatter(data.Education,data.Income)
plt.plot(X.numpy(),model(X).data.numpy())
plt.xlabel("受教育年限")
plt.ylabel("工资")
plt.show()
完整代码:

import torch
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from torch import nn
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
data = pd.read_csv('dataset/Income1.csv')
print(type(data))
data.info()
data
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 雅黑字体
plt.scatter(data.Education,data.Income)
plt.xlabel("受教育年限")
plt.ylabel("工资")
plt.show()
X = torch.from_numpy(data.Education.values.reshape(-1,1).astype(np.float32) ) #转换数据类型
Y = torch.from_numpy(data.Income.values.reshape(-1,1).astype(np.float32) ) #转换数据类型
model = nn.Linear(1,1) #w@input+b 等价于model(input)
loss_fn = nn.MSELoss() #定义均方损失函数
opt = torch.optim.SGD(model.parameters(),lr=0.00001)
for epoch in range(200):
for x, y in zip(X,Y):
y_pred = model(x) #使用模型预测
loss = loss_fn(y,y_pred) #根据预测计算损失
opt.zero_grad() #进行梯度清零
loss.backward() #求解梯度
opt.step() #优化模型参数
print(f'epoch {epoch + 1}, loss {loss.sum():f}')
model.weight
model.bias
type(model.weight.detach().numpy())
plt.scatter(data.Education,data.Income)
plt.plot(X.numpy(),model(X).data.numpy())
plt.xlabel("受教育年限")
plt.ylabel("工资")
plt.show()
看完点个关注呗!!(总结不易)
